天津市滨海新区经济技术开发区国际学校2024-2025学年九年级上学期期中考试数学试题

这是一份天津市滨海新区经济技术开发区国际学校2024-2025学年九年级上学期期中考试数学试题，共22页。试卷主要包含了本卷共12题，共36分．等内容，欢迎下载使用。
命题人：边庆岭 审卷人：王梓懿
本试卷分为第I卷（选择题）、第Ⅱ卷（非选择题）两部分．第I卷为第1页至第3页，第Ⅱ卷为第4页至第8页．试卷满分120分．考试时间100分钟．
答卷前，考生务必将自己的姓名、考生号、考场号、座位号填写在“答题卡”上．答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效．考试结束后，将“答题卡”交回．
祝各位考生考试顺利！
第I卷
注意事项：
1.每题选出答案后，用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点．
2.本卷共12题，共36分．
一、选择题（本题共12小题，36分）
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录，下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”，其中既是轴对称图形，又是中心对称图形的是（ ）
A. B.
C. D.
2.下列事件是必然事件的是（ ）
A.明天早上会下雨
B.掷一枚硬币，正面朝上
C.任意一个三角形，它的内角和等于
D.一个图形旋转后所得的图形与原图形不全等
3.如果反比例函数图象在二，四象限，那么的取值范围是（ ）
A. B. C. D.
4.将抛物线先向右平移2个单位，再向下平移3个单位，所得新抛物线的解析式为（ ）
A. B.
C. D.
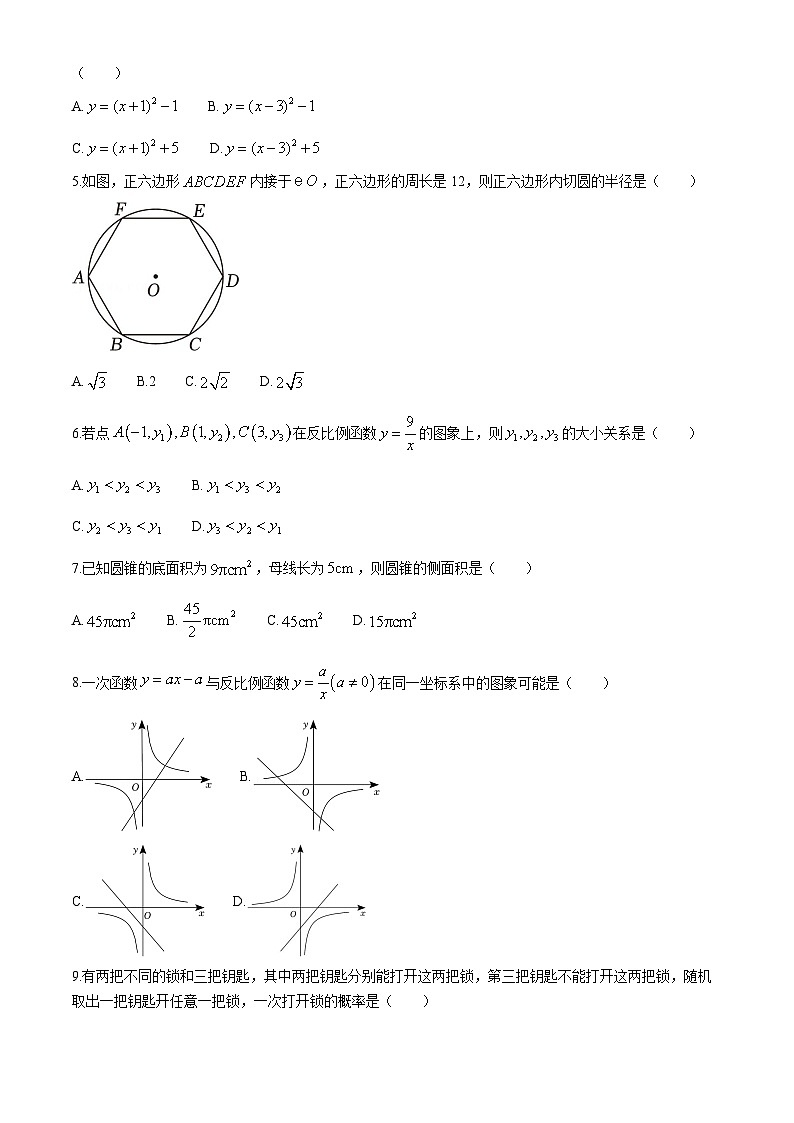
5.如图，正六边形内接于，正六边形的周长是12，则正六边形内切圆的半径是（ ）
A. B.2 C. D.
6.若点在反比例函数的图象上，则的大小关系是（ ）
A. B.
C. D.
7.已知圆锥的底面积为，母线长为，则圆锥的侧面积是（ ）
A. B. C. D.
8.一次函数与反比例函数在同一坐标系中的图象可能是（ ）
A. B.
C. D.
9.有两把不同的锁和三把钥匙，其中两把钥匙分别能打开这两把锁，第三把钥匙不能打开这两把锁，随机取出一把钥匙开任意一把锁，一次打开锁的概率是（ ）
A. B. C. D.
10.如图，四边形内接于，点是的内心，，点在的延长线上，则的度数为（ ）
A. B. C. D.
11.如图，将绕点逆时针旋转后得到，点的对应点分别为，点恰好在边上，且点在的延长线上，连接，若，则下列结论一定正确的是（ ）
A. B.
C.旋转角是 D.
12.如图，是抛物线形拱桥，当拱桥顶端离水面时，水面的宽度为．有下列结论：
①当水面宽度为时，水面下降了；
②当水面下降时，水面宽度为；
③当水面下降时，水面宽度增加了．
其中，正确的是（ ）
A.0 B.1 C.2 D.3
第II卷
注意事项：
1.用黑色墨水的钢笔或签字笔将答案写在“答题卡”上．
2.本卷共13题，共84分．
二、填空题（共6小题，18分）
13.在一个不透明的袋中有6个只有颜色不同的球，其中4个黑球和2个白球．从袋中任意摸出一个球，是白球的概率为__________．
14.如图，是的内接三角形，若，则__________．
15.如图，在平面直角坐标系中，点在反比例函数（为常数，）的图象上，过点作轴的垂线，垂足为，连接．若的面积为5，则__________．
16.如图，分别与相切于点，点为劣弧上的点，过点的切线分别交于点．若，则的周长为__________．
17.若关于的一元二次方程的两个实数根，且满足，则的值为__________．
18.如图，在每个小正方形的边长为1的网格中，圆经过格点，与格线交于点．
（1）__________（度）．
（2）若点在圆上，满足，请利用无刻度的直尺，在圆上画出点，使，并简要说明点的位置是如何找到的（不要求证明）__________．
三、解答题（本题共7小题，66分）
19.解方程：
（1）
（2）．
20.二次函数（为常数，）的自变量与函数值的部分对应值如下表：
（1）该二次函数解析式为__________，__________，__________；
（2）请在给出的平面直角坐标系中，画出二次函数的图象；
（3）根据图象直接回答下列问题：
①当__________时，有最__________值（填“大”或“小”），该最值是__________；
②若该二次函数图象上有两点和，比较和的大小，其结果是：__________；
③当时，的值为__________；
④当时，则的取值范围是__________．
21.如图，是的直径，为上一点，和过点的切线互相垂直，垂足为交于点．
（1）求证：平分；
（2）求的半径．
22.已知中，为的弦，直线与相切于点．
（1）如图①，若，直径与相交于点，求和的大小；
（2）如图②，若，垂足为与相交于点，求线段的长．
23.如图，点分别在菱形的四条边上，且，连接，得到四边形．
（1）求证：四边形是矩形；
（2）设，当为何值时，矩形的面积最大？
24.已知矩形，将矩形绕顺时针旋转，得到矩形，点的对应点是点，点的对应点是点，点的对应点是点．
（1）如图①；当时，连接，求的长；
（2）如图②，当边经过点时，延长交于点，求的长；
（3）连接，点是的中点，连接，在旋转过程中，线段的最大值__________．
25.已知抛物线（是常数，）的顶点为，与轴相交于点和点．
（1）若，
①求点的坐标；
②直线（是常数，）与抛物线相交于点，与相交于点，当取得最大值时，求点的坐标；
（2）若，直线与抛物线相交于点是轴的正半轴上的动点，是轴的负半轴上的动点，当的最小值为5时，求点的坐标．
2024-2025（1）国际学校九年级阶段性学情诊断卷答案
一、选择题（共12小题）
1.【解答】解：A.是轴对称图形，但不是中心对称图形，故A选项不合题意；
B.是轴对称图形，不是中心对称图形，故B选项不合题意；
C.不是轴对称图形，也不是中心对称图形，故C选项不合题意；
D.既是轴对称图形，又是中心对称图形，故D选项合题意；故选：D.
2.【解答】解：A、明天早上会下雨，是随机事件，不符合题意；
B、掷一枚硬币，正面朝上，是随机事件，不符合题意；
C、任意一个三角形，它的内角和等于，是必然事件，符合题意；
D、一个图形旋转后所得的图形与原图形不全等，是不可能事件，不符合题意；
故选：C.
3.【解答】解：因为反比例函数图象在二，四象限，
所以，
解得．
故选：C.
4.【解答】解：将抛物线先向右平移2个单位，再向下平移3个单位，
所得新抛物线的解析式为，即，
故选：B.
5.【解答】解：连接，过点作于点．
多边形是正六边形，
，
，
是等边三角形，
，
正六边形的周长是12，
的半径是2，
正六边形内切圆的半径是．
故选：A.
6.【解答】解：，
在每一象限内，随的增大而减小，
，
，
故选：B.
7.【解答】解：设圆锥的底面半径为，
由题意，
，
圆锥的侧面积，
故选：D.
8.【解答】解：当时，直线经过第一、三、四象限，双曲线经过第一、三象限，故A符合题意；
当时，直线经过第一、二、四象限，双曲线经过第二、四象限，没有符合题意的．
故选：A.
9.【解答】解：根据题意列表得：
所有等可能的情况有6种，其中随机取出一把钥匙开任意一把锁，一次打开锁的2种，
则随机取出一把钥匙开任意一把锁，一次打开锁的概率是；
故选：D.
10.【解答】解：点是的内心，
，
，
，
又四边形内接于，
，
故选：C．
11.【解答】解：将绕点逆时针旋转后得到，
，
，
，
，
，即旋转角为，
，
，
，
与不平行，
，
，
故选：A.
12.【解答】解：以线段所在的直线为轴，以的垂直平分线为轴建立平面直角坐标系．
由题意得：点的坐标为，点的坐标为．
设抛物线解析式为：．
．
解得：．
抛物线解析式为：．
①当水面宽度为时，．
．
当水面宽度为时，水面下降了．
故①正确，符合题意；
②当水面下降时，．
解得：．
水面宽度为：．
故②正确，符合题意；
③当水面下降时，．
解得：．
水面宽度为：．
水面宽度增加了．
故③正确，符合题意；
正确的有3个．
故选：D.
二、填空题（共6小题）
13.
【解答】解：袋子中共有6个小球，其中白球有2个，
从袋中任意摸出一个球，是白球的概率为．
故答案为：．
14.．
【解答】解：连接，
，
，
，
，
故答案为：62.
15.10.
【解答】解：点在反比例函数的图象上，轴于，
根据反比例函数比例系数的几何意义得：，
，
的面积为5，
，
，
．
故答案为：10.
16.20.
【解答】解：是的切线，，
，
的周长．
故答案为：20.
17.【解答】解：由根与系数的关系，得，
所以，即，
解得或，
因为时，
所以，
解得：，故舍去，
故答案为：．
18.【解答】解：（1）；
故答案为：90；
（2）如图，取圆与格线的交点，连接，它们的交点为圆心，延长交于点在，则点为所作．
三、解答题（共7小题）
19.【解答】解：（1），
，
，
，
或，
解得；
（2），
，
，
，
或，
．
20.【解答】解：（1）把代入得：，
解之得：，
该函数的解析式为：，
把分别代入得：
，
故答案为：；
（2）如图所示：
（3）①由图可得，当时，函数值有最小值，最小值为，故答案为：，小，；
②由图象可得，抛物线对称轴为直线，抛物线开口向上，
抛物线上点离对称轴越远，函数值越大，
点离对称轴较远，
，
故答案为：；
③当时，，
抛物线对称轴为直线，
，即，
当时，的值为，
故答案为：、5；
④抛物线的对称轴为直线，开口向上，
的最小值是，
由图可得，当时，的取值范围是，
故答案为：．
21.【解答】．（1）证明：如图1，连接．
和过点的切线互相垂直，垂足为，
，
是过点的切线，
．
，
，
，
，
，
，
．
即平分；
（2）如图2，过点作，垂足为．
，
由（1）知，，
四边形是矩形，
，
在中，，，
即的半径为．
22.【解答】解：（1），
，
，
，
直线与相切于点为的直径，
，
，
，
，
，
；
（2）如图，连接．
同（1），得，
，
，
，
，
，
在中，，
．
23.【解答】（1）证明：，
，
同理，，
，
又菱形中，，
，
，
，
同理，，
四边形是矩形；
（2）如图，连接四边形是菱形，，
和是等边三角形，
，
，
则菱形的面积是：，
设，则，
，
，
，
是等边三角形，
在中，，
则矩形的面积，
当时，矩形的面积最大，
．
24.【解答】解：（1）连接，如图①，
是矩形，
，
又，
，
由旋转可得，
；
（2）如图②，连接，
由题意可知，在中，，
根据勾股定理得，
，
，
又，
，
，
；
（3）连接交于点，连接，如图③，
四边形是矩形，
，
点是的中点，
是的中位线，
，
点在以为圆心，以为半径的圆上运动，
根据直径是圆中最长的弦可知，当为直径时，即点与点重合时，最大，最大为：，
故答案为：．
25.【解答】解：（1）①若，
则抛物线，
抛物线与轴相交于点，
，解得，
抛物线为，
顶点的坐标为（）；
②当时，，
解得，
，
设直线的解析式为，
，解得，
直线的解析式为，
直线（是常数，与抛物线相交于点，与相交于点，设点，则，
，
当时，取得最大值1，
此时，点，则；
（2）抛物线与轴相交于点，
，
又，
，
抛物线的解析式为．
，
顶点的坐标为，
直线与抛物线相交于点，
点的坐标为，
作点关于轴的对称点，作点关于轴的对称点，
得点的坐标为，点的坐标为，
当满足条件的点落在直线上时，取得最小值，此时，．
延长与直线相交于点，则．
在中，．
．
解得（舍）．
点的坐标为，点的坐标为．
直线的解析式为．
点，点．0
1
2
3
4
0
锁1
锁2
钥匙1
（锁1，钥匙1）
（锁2，钥匙1）
钥匙2
（锁1，钥匙2）
（锁2，钥匙2）
钥匙3
（锁1，钥匙3）
（锁2，钥匙3）
x
0
2
4
5
y
0
0