人教版（2024）七年级下册5.2.1 平行线精品测试题

这是一份人教版（2024）七年级下册5.2.1 平行线精品测试题，文件包含人教版初中数学七年级下册同步讲与练专题55重点突破训练相交线平行线类型题举例原卷版docx、人教版初中数学七年级下册同步讲与练专题55重点突破训练相交线平行线类型题举例解析版docx等2份试卷配套教学资源，其中试卷共165页， 欢迎下载使用。
典例体系（本专题99题123页）
考点1：相交线所成的角
典例：（2022春·湖北荆州·七年级统考期末）如图，直线AB，CD相交于点O，OB平分∠EOD．
(1)若∠BOD＝30°，求∠EOC的度数；
(2)若∠BOD∶∠EOC＝1∶3，求∠AOD的度数；
(3)在（2）的条件下，画射线OF，若∠COF=90°，请直接写出∠BOF的度数．
【答案】(1)
(2)
(3)的度数为或
【分析】（1）先根据角平分线的定义可得，再根据平角的定义即可得；
（2）先根据可得，再根据平角的定义可得，然后根据邻补角的定义即可得；
（3）分两种情况讨论：①射线在的上方和②射线在的下方，先利用平角的定义可得，再根据角的和差即可得．
（1）解：因为平分，，所以，所以．
（2）解：因为，所以，因为，所以，所以，所以．
（3）解：由题意，分以下两种情况：①如图，当射线在的上方时，
因为，所以，所以；②如图，当射线在的下方时，
因为，所以，所以，综上，的度数为或．
方法或规律点拨
本题考查了与角平分线有关的计算、邻补角、平角，熟练掌握角平分线的运算是解题关键．
巩固练习
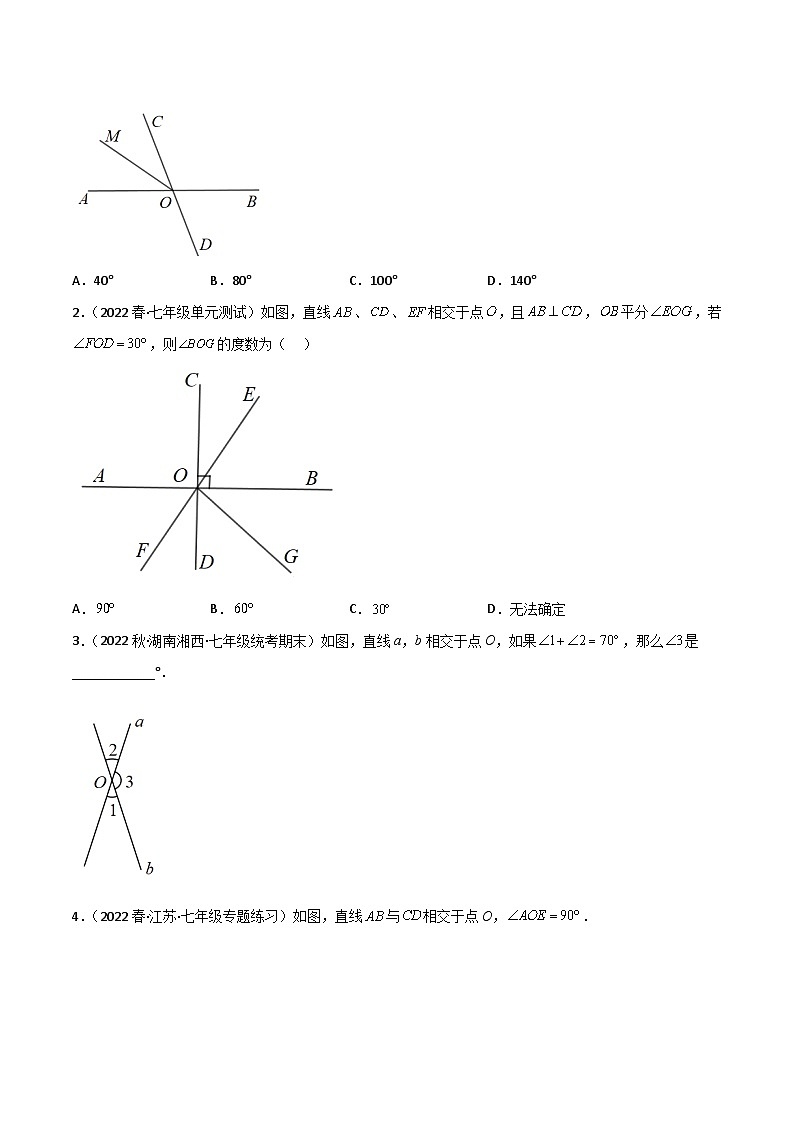
1．（2022秋·河北邢台·七年级统考期末）如图，直线AB，CD相交于点O，射线OM平分∠AOC，若∠BOD＝80°，则∠BOM等于（ ）
A．40°B．80°C．100°D．140°
【答案】D
【分析】根据对顶角相等和平角的定义即可求出∠AOC和∠BOC，然后根据角平分线的定义即可求出∠COM，从而求出结论．
【详解】解：∵
∴∠AOC=∠BOD=80°，∠BOC=180°－∠BOD=100°
∵平分
∴∠COM=∠AOC=40°
∴∠BOM=∠COM＋∠BOC=140°
故选:D．
【点睛】此题考查的是角的和与差，掌握对顶角相等、平角的定义和角平分线的定义是解决此题的关键．
2．（2022春·七年级单元测试）如图，直线、、相交于点，且，平分，若，则的度数为（ ）
A．B．C．D．无法确定
【答案】B
【分析】根据对顶角相等可以得到，再根据垂直的性质可以得到，即可求出的度数，再根据角平分线的定义即可得出答案．
【详解】解：∵，
∴
∵，
∴
∴
∵平分，
∴
故选B．
【点睛】本题考查了角度的和差倍分，垂直的定义，角平分线的定义，熟练掌握以上性质并找出角度之间的关系是本题的关键．
3．（2022秋·湖南湘西·七年级统考期末）如图，直线a，b相交于点O，如果，那么是____________°．
【答案】145
【分析】根据对顶角相等求出∠1，再根据互为邻补角的两个角的和等于180°列式计算即可得解．
【详解】解：∵，（对顶角相等），
∴，
∵∠1与∠3互为邻补角，
∴．
故答案为：．
【点睛】本题考查了对顶角相等的性质，邻补角的定义，是基础题，熟记概念与性质并准确识图是解题的关键．
4．（2022春·江苏·七年级专题练习）如图，直线与相交于点O，．
(1)如果，求和的度数；
(2)如果，求的度数．
【答案】(1)；
(2)
【分析】（1）根据角的和差与对顶角即可求解；
（2）根据已知条件可得，从而可求得，根据邻补角即可求的度数．
【详解】（1）∵，
∴，
∵与是对顶角，
∴．
（2）∵，
∴．
又∵，
∴，
∴，
∴．
【点睛】本题考查了对顶角，邻补角，以及角的和差计算，解答的关键是熟记对顶角与邻补角的定义的掌握与应用．
5．（2022秋·重庆·七年级校联考阶段练习）如图，直线，相交于点O，平分，平分．
(1)判断与的位置关系，并进行证明．
(2)若，求的度数．
【答案】(1)，证明见解析
(2)
【分析】（1）由平分，平分，得到，，根据邻补角互补可得出，进而可得出，由此即可证出；
（2）由，，得到，由对顶角相等，可求出，根据平分，平分，可得出以及，根据邻补角互补结合，可求出的度数．
【详解】（1）．
证明：∵平分，平分，
∴，，
∵，
∴，
∴．
（2）∵，，
∴，
∴，
∵，
∴，
∵平分，平分，
∴，．
∵，
∴，
∴．
【点睛】本题考查了对顶角相等，邻补角互补，角平分线的定义，熟练掌握知识点是解题的关键．
6．（2021春·湖北荆州·七年级统考期末）如图，O是直线AB上一点，平分．
(1)若，请求出的度数；
(2)若和互余，且，请求出的度数．
【答案】(1)
(2)
【分析】(1)根据角平分线的定义，即可求得；
(2)首先根据和互余，可得，再根据，可求得，可求得，据此即可求得．
（1）
解：，平分，，
；
（2）
解：和互余，
，
∴，
平分，
，
．
【点睛】本题考查了与角平分线有关的计算，准确找到角与角之间的关系是解决本题的关键．
7．（2022·全国·七年级专题练习）如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE．
(1)若∠AOC=76°，求∠BOF的度数；
(2)若∠BOF=36°，求∠AOC的度数；
【答案】(1)∠BOF=33°
(2)∠AOC=72°
【分析】（1）先根据对顶角相等求出∠BOD=76°，再由角平分线定义得∠DOE=∠BOE=38°，由邻补角得∠COE=142°，再根据角平分线定义得∠EOF=71°，从而可得结论．
（2）利用角平分的定义得出，进而表示出各角求出答案．
【详解】（1）∵∠AOC、∠BOD是对顶角，
∴∠BOD=∠AOC=76°，
∵OE平分∠BOD，
∴∠DOE=∠BOE=∠BOD=38°
∴∠COE=142°，
∵OF平分∠COE．
∴∠EOF=∠COE=71°，
又∠BOE+∠BOF=∠EOF，
∴∠BOF=∠EOF−∠BOE=71°−38°=33°，
（2）∵OE平分∠BOD，OF平分∠COE，
∴，
∴设，则，
故，，
则，
解得，
故∠AOC=72°．
【点睛】本题考查了角平分线的定义和对顶角的性质，解决本题的关键是掌握对顶角的定义（从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线）．
8．（2022春·广东湛江·九年级校考期中）如图，已知O为直线上一点，过点O向直线上引三条射线，且平分．
(1)若平分，求的度数；
(2)若，，求的度数．
【答案】(1)
(2)
【分析】（1）利用角平分线的定义，可证得，，再根据邻补角的定义，就可求出的度数．
（2）根据已知及角平分线的定义，用含的代数式表示出，再根据，建立关于的方程，求解即可．
（1）
解：∵平分，OE平分∠BOC，
∴，，
∵
∴
答：的度数为．
（2）
解：∵，
∴
∵平分
∴
∵
∴
解之：
答：的度数为．
【点睛】本题考查了角平分线定义、平角以及角的计算等知识，熟练掌握角平分线定义是解题的关键．
9．（2022秋·福建龙岩·七年级校考阶段练习）如图，直线AB、CD相交于点O，∠DOE＝∠BOD，OF平分∠AOE．
(1)判断OF与OD的位置关系，并说明理由；
(2)若∠AOC：∠AOD＝1：5，求∠EOF的度数．
【答案】(1)OF⊥OD，理由见解析；
(2)∠EOF＝60°
【分析】（1）利用角平分线的定义结合已知求出∠FOD＝90°即可得出答案；
（2）求出∠AOC的度数，再利用对顶角的性质和角平分线的定义求出∠BOD＝∠AOC＝∠EOD＝30°，进而得出∠EOF的度数．
（1）
解：OF⊥OD，
理由：∵OF平分∠AOE，
∴∠AOF＝∠FOE，
∵∠DOE＝∠BOD，
∴∠AOF＋∠BOD＝∠FOE＋∠DOE＝×180°＝90°，即∠FOD＝90°，
∴OF与OD的位置关系是OF⊥OD；
（2）
∵∠AOC：∠AOD＝1：5，
∴∠AOC＝×180°＝30°，
∴∠BOD＝∠AOC＝∠EOD＝30°，
∴∠AOE＝120°，
∴∠EOF＝∠AOE＝60°．
【点睛】此题主要考查了角平分线的定义以及邻补角的性质，正确得出各角之间的关系是解题关键．
10．（2022春·七年级课时练习）如图，直线AB，CD相交于点O，OB平分∠EOD．
(1)若∠BOE：∠EOC＝1：4，求∠AOC的度数；
(2)在（1）的条件下，画OF⊥CD，请直接写出∠EOF的度数．
【答案】(1)
(2)或
【分析】（1）设，则，先根据角平分线的定义可得，，再根据邻补角的定义求出的值，从而可得的度数，然后根据对顶角相等即可得；
（2）先求出，再分①点在的上方和②点在的下方两种情况，根据角的和差即可得．
【详解】（1）解：由题意，设，则，
平分，
，，
，
，
解得，
，
由对顶角相等得：．
（2）解：由（1）可知，，
，
，
由题意，分以下两种情况：
①如图，当点在的上方时，
则；
②如图，当点在的下方时，
则；
综上，的度数为或．
【点睛】本题考查了与角平分线有关的计算、对顶角相等、一元一次方程的应用，较难的是题（2），正确分两种情况讨论是解题关键．
11．（2022秋·山东济宁·七年级统考期末）如图，直线 AB，CD相交于点O，∠BOC=80°，OE是∠BOC的平分线，OF是OE的反向延长线．
(1)求∠2、∠3的度数；
(2)说明 OF平分∠AOD的理由．
【答案】(1)∠2＝100°，∠3＝40°
(2)理由见详解
【分析】（1）根据邻补角的性质，得∠2＝180°﹣80°＝100°，再求出∠AOD的度数，根据角平分线的性质求出∠3；
（2）根据对顶角相等以及角平分线的定义得出∠AOF＝∠DOF即可．
（1）
解：∵∠2和∠BOC互为补角，且∠BOC＝80°，
∴∠2＝180°﹣80°＝100°，
∵OE是∠EOC的平分线，
∴∠1＝∠EOC＝ ∠BOC＝40°，
∵OF是OE的反向延长线，
∴∠3＝∠EOC＝40°，
（2）
理由如下：
由（1）得∠3＝∠EOC＝40°，
又∵∠AOF＝∠1＝40°，
∴∠AOF＝∠DOF，
∴OF平分∠AOD．
【点睛】本题考查角平分线的定义，对顶角、邻补角，理解角平分线的定义，掌握对顶角相等以及邻补角的性质是解题的关键．
12．（2022秋·湖北孝感·七年级统考期中）如图，直线与相交于点，．
(1)若，判断与的位置关系，并证明；
(2)若，求的度数．
【答案】(1)
(2)
【分析】（1）根据垂直的定义求解即可；
（2）根据角的和差及“对顶角相等”求解即可．
（1）
，理由如下：
，
，
，
，
，
即，
；
（2）
，，
，
，
，
，
．
【点睛】此题考查了对顶角、邻补角，熟记对顶角、邻补角的概念是解题的关键．
13．（2022春·陕西安康·七年级统考期末）如图，点在直线上，与互补，平分．
(1)若，则的度数为______；
(2)若，求的度数．
【答案】(1)
(2)
【分析】（1）根据互补的定义，邻补角以及角平分线的定义解答即可；
（2）根据互补的定义和角平分线的定义列出方程解答即可．
（1）
解：∵点在直线上，，
∴，
∵与互补，
∴，
∵平分，
∴，
∴．
故答案为：．
（2）
设为x，
∵点在直线上，
∴与互补，
∵与互补，
∴，
∵平分，
∴，
∴，
∵与互补，
即，
，
解得：，
∴．
∴的度数为．
【点睛】本题考查补角问题，涉及互补的定义，邻补角，等角的补角相等，角平分线的定义．理解和掌握互补的定义，邻补角以及角平分线的定义是解题的关键．
14．（2022春·七年级课时练习）如图1，点为直线上一点，过点作射线，使．将一直角三角板的直角顶点放在点处，一边在射线上，另一边在直线的下方．
(1)将图1中的三角板绕点处逆时针旋转至图2，使一边在的内部．且恰好平分，求的度数；
(2)在图3中，延长线段得到射线，判断是否平分，请说明理由．
(3)将图1中的三角板绕点按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，第秒时，直线恰好平分锐角，则的值为______．（直接写出答案）
【答案】(1)
(2)平分；理由见解析
(3)30或12秒
【分析】（1）由角的平分线的定义和等角的余角相等求解；
（2）先由对顶角性质得=30°，再由，得，从而得出结论；
（3）由∠BOC=120°可得∠AOC=60°，则∠AON=30°或∠NOR=30°，即顺时针旋转300°或120°时ON平分∠AOC，据此求解．
【详解】（1）解：∵，
∴，
∵恰好平分，
∴，
∴，
∴；
（2）解：∵（对顶角），．
∴，
又∵，
∴．
∴
∴平分
（3）解：30或12．
设三角板绕点旋转的时间是秒，
∵，
∴，
如图，当的反向延长线平分时，
，
∴，
∴旋转的角度是，
∴，
∴；
如图，当平分时，
，
∴旋转的角度是，
∴，
∴，
综上，或，
即此时三角板绕点旋转的时间是30或12秒．
【点睛】此题考查了角的计算，关键是应该认真审题并仔细观察图形，找到各个量之间的关系，是解题的关键．
15．（2022秋·浙江台州·七年级校联考阶段练习）如图，直线CD，EF相交于点O，射线OA在∠COF的内部，∠DOF=∠AOD．
(1)如图1，若∠AOC=120°，求∠EOC的度数；
(2)如图2，若∠AOC=α（60°