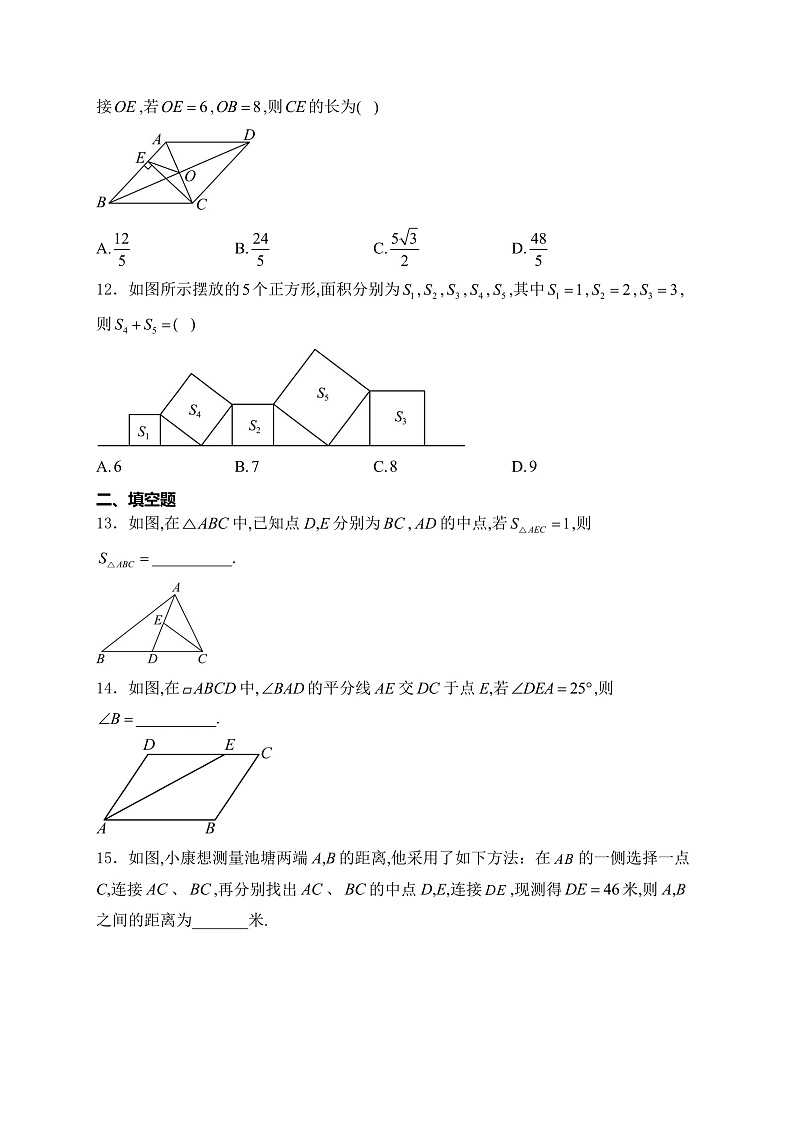
贵州省黔西南州兴仁市三校（金成、黔龙、黔峰）2025届九年级上学期期中考试数学试卷(含答案)

贵州省黔西南州兴仁市三校（金成、黔龙、黔峰）2025届九年级上学期期中考试数学试卷学校：___________姓名：___________班级：___________考号：___________一、单选题1．下列各组数中,哪一组是勾股数( )A.1,2,4 B.1,3,5 C.3,4,7 D.5,12,132．如图,将一直角三角形放于一对平行线上,量得则( )A. B. C. D.3．如图所示,小明试卷上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与试卷原图完全一样的三角形,那么两个三角形完全一样的依据是( )A. B. C. D.4．下面给出了四组四边形中,,,的度数之比,其中能确定四边形为平行四边形的是( )A. B.C. D.5．如图,矩形中,O是对角线的中点,连接.若,,则的长为( )A.7 B.8 C.9 D.106．如图,是的平分线,且,,则的度数为( )A. B. C. D.7．下列命题中,错误的是( )A.两条对角线相等的平行四边形是矩形 B.两条对角线互相垂直的四边形是菱形C.两条对角线互相垂直的矩形是正方形 D.两条对角线互相平分的四边形是平行四边形8．如图,在中,,以顶点A为圆心,适当长为半径画弧,分别交于点M、N,再分别以点M,N为圆心,大于的长为半径画弧,两弧交于点P,作射线交边于点D,若,则点D到的距离是( )A.6 B.8 C.10 D.129．一个圆桶底面直径为,高,则桶内所能容下的最长木棒为( )A.20cm B.50cm C.40cm D.45cm10．如图,E,F,G,H分别为四边形边,,,的中点,要使四边形为矩形,应添加的条件是( )A. B. C. D.11．如图,菱形的对角线,相交于点O,过点C作,交于点E,连接,若,,则的长为( )A. B. C. D.12．如图所示摆放的个正方形,面积分别为,,,,,其中,,,则( )A. B. C. D.二、填空题13．如图,在中,已知点D,E分别为,的中点,若,则__________.14．如图,在中,的平分线交于点E,若,则__________.15．如图,小康想测量池塘两端A,B的距离,他采用了如下方法：在的一侧选择一点C,连接、,再分别找出、的中点D,E,连接,现测得米,则A,B之间的距离为_______米.16．菱形中,,点P为对角线上一点,点E是边上一点,连接,,若的最小值是,则菱形的边长为_____.三、解答题17．已知：,,,求证：.18．某段河流的两岸是平行的,某数学兴趣小组在老师的带领下不用涉水过河就能测得河的宽度.他们是这样做的：①在河流的岸边点B处,选对岸正对的一棵树A；②沿河岸直行处有一棵树C,继续前行到达点D处；③从点D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的点E处时,停止行走；④测得的长为.根据测量数据求河的宽度.19．我市某中学有一块四边形的空地(如图所示),为了绿化环境,学校计划在空地上种植草皮,经测量,,,,.(1)求出空地的面积；(2)若每种植1平方米草皮需要200元,问总共需投入多少元？20．如图,平行四边形中,对角线,相交于点O,E、F分别是、的中点.求证：.21．如图所示,在长方形中,,,若将长方形沿折叠,使点D落在边上的点F处,求线段的长.22．如图,在矩形中,O为对角线的中点,过点O作直线分别与矩形的边,交于M、N两点,连接,.(1)求证：四边形是平行四边形；(2)若且,,求四边形的面积.23．如图,在中,,,延长至点E,使,连接,交于点F,连接,,.求证：四边形是矩形.24．在矩形中,,,E、F分别是、上两点,并且垂直平分,垂足为O.(1)连接、.说明四边形为菱形；(2)求的长.25．如图,四边形、都是正方形,连接、.(1)判断线段、的关系并证明.(2)连接、、、,顺次连接各边中点G、H、Q、N,试判断四边形的形状,并说明理由.参考答案1．答案：D解析：A、,不是勾股数,不符合题意；B、,不是勾股数,不符合题意；C、,不是勾股数,不符合题意；D、,是勾股数,符合题意；故选：D.2．答案：C解析：两条平行线记为a,b,∵,∴,∴,∴,故选：C.3．答案：A解析：因为试卷上的三角形的两个角和这两个角所夹的边没有被墨迹污染,所以利用“”画出一个与试卷原图完全一样的三角形.故选：A.4．答案：D解析：,,,∴四边形是平行四边形,故选：D.5．答案：D解析：四边形为矩形,,,,,,,,故选：D.6．答案：B解析：是的平分线,,,,,.故选：B.7．答案：B解析：A、两条对角线相等的平行四边形是矩形,正确,不合题意；B、两条对角线互相垂直的平行四边形是菱形,故选项错误,符合题意；C、两条对角线互相垂直的矩形是正方形,正确,不合题意；D、两条对角线互相平分的四边形是平行四边形,正确,不合题意；故选：B.8．答案：C解析：由作法得平分,∴点D到和的距离相等,∵,∴,∴点D到的距离为的长,即点D到的距离为10,∴点D到的距离为10.故选：C.9．答案：C解析：如图,AC为圆桶底面直径,∴,,∴线段AB的长度就是桶内所能容下的最长木棒的长度,∴.故桶内所能容下的最长木棒的长度为.故选：C.10．答案：D解析：如图所示,连接,,∵E,F,G,H分别为四边形边,,,的中点,∴,,,分别是,,,的中位线,∴,,,,∴四边形是平行四边形,∴要使四边形是矩形,那么,则,故选：D.11．答案：D解析：∵四边形是菱形,∴,.在中,是斜边上的中线,∴,∴.在中,.∴,即,解得.故选：D.12．答案：C解析：如图,,,,又,,,,,,同理可得：,,故选：C.13．答案：4解析：点E为的中点,,,点D为的中点,.故答案为：4.14．答案：/130度解析：∵四边形是平行四边形,∴,,∴,∵平分,∴,∴,∴,故答案为：.15．答案：92解析：是AC的中点,E是BC的中点,是的中位线,,米,米.16．答案：解析：连接、,根据菱形的对称性可得,∴,当时,可知最短,此时点C,P,E三点共线,如图,∵的最小值是,∴,∵,∴,∵,∴,∴,∴菱形的边长为2,故答案为：2.17．答案：证明见解析.解析：证明：∵,∴,∴,∵,∴,∵在和中,,∴,∴.18．答案：解析：由题意知,,在和中,,∴,,∵,∴,答：河宽为.19．答案：(1)(2)元解析：(1)如图所示,连接,在中,,,,∴,∵,,∴,∴是直角三角形,且,∴(2)元,∴总共需投入元.20．答案：见解析解析：证明：∵四边形是平行四边形,∴,,∵E、F分别是、的中点,,,∴,∴四边形是平行四边形,∴.21．答案：解析：四边形是长方形,,,,由轴对称的性质,可得：,,在中,根据勾股定理,可得：,,设,则,在中,根据勾股定理,可得：,即：,解得：,线段的长是.22．答案：(1)见解析(2)5解析：(1)证明：四边形是矩形,,,,为对角线的中点,,在和中,,,,又,四边形为平行四边形；(2)由(1)知：四边形为平行四边形,,平行四边形是菱形,,四边形是矩形,,,,,设的长度为x,则,,,,,解得,即,.23．答案：证明见解析解析：证明：∵四边形是平行四边形,∴,,,∵,∴,∴四边形是平行四边形,∴,,∵,∴,∴,∴,∴四边形是矩形.24．答案：(1)证明见解析(2)解析：(1)证明：∵四边形矩形,∴,∴,∵平分,∴,在和中,,∴,∴,∴四边形是平行四边形,∵,∴四边形是菱形.(2)∵四边形是菱形,∴设,则在中,,∴解得：,∴的长为.25．答案：(1),,理由见解析(2)四边形的形状是正方形,理由见解析解析：(1),,理由如下：设与交于点O,与交于点H,如图所示：四边形、都是正方形,,,,,在和中,,,,,,,,即；(2)四边形是正方形,理由如下：顺次连接、、、的中点G、H、Q、N,如图所示,∴,,,∴四边形为平行四边形,,∴,,∴,即,∴四边形为矩形,∵,∴,四边形是正方形.