

2023~2024学年山东省济宁市梁山县八年级(上)期中数学试卷(解析版)
展开
这是一份2023~2024学年山东省济宁市梁山县八年级(上)期中数学试卷(解析版),共16页。试卷主要包含了精心选一选,相信自己的判断力!等内容,欢迎下载使用。
一、精心选一选,相信自己的判断力!(本题共12小题,每小题3分)
注意可以用各种不同的方法来解决你面前的选择题哦!
1. 第19届亚运会于2023年9月23日~2023年10月8日在中华人民共和国杭州市举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案,其中可以看作是轴对称图形的是( )
A. B.
C. D.
【答案】D
【解析】、选项中的图形不是轴对称图形,不符合题意;
B、选项中图形不是轴对称图形,不符合题意;
C、选项中的图形不是轴对称图形,不符合题意;
D、选项中的图形可以看作是轴对称图形,符合题意;
故选:.
2. 用下列长度三根木棒首尾相接,能做成三角形框架的是( )
A. 、、B. 、、
C. 、、D. 、、
【答案】A
【解析】A、,能组成三角形,故A符合题意;
B、,不能组成三角形,故B不符合题意;
C、,不能组成三角形,故C不符合题意;
D、,不能组成三角形,故D不符合题意.
故选:A.
3. 人字梯中间一般会设计一“拉杆”,这样做的道理是( ).
A. 三角形具有稳定性.B. 两直线平行,内错角相等.
C. 两点之间,线段最短.D. 垂线段最短.
【答案】A
【解析】人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:A.
4. 在平面直角坐标系中,点关于轴对称的点的坐标是( )
A. B. C. D.
【答案】C
【解析】点关于轴对称的点的坐标为.
故选:C.
5. 一个等腰三角形的两边长分别为4,8,则它的周长为( )
A. 12B. 16C. 16或20D. 20
【答案】D
【解析】等腰三角形的两边长分别为4和8,
当腰长是4时,则三角形的三边是4,4,8,不满足三角形的三边关系;
当腰长是8时,三角形的三边是8,8,4,三角形的周长是20.
故选:D.
6. 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,若添加下列一个条件后,仍然不能证明△ABC≌△DEF,则这个条件是( )
A. ∠A=∠DB. BC=EFC. ∠ACB=∠FD. AC=DF
【答案】D
【解析】∵∠B=∠DEF,AB=DE,
∴添加∠A=∠D,利用ASA可得△ABC≌△DEF;
∴添加BC=EF,利用SAS可得△ABC≌△DEF;
∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF;
故选:D.
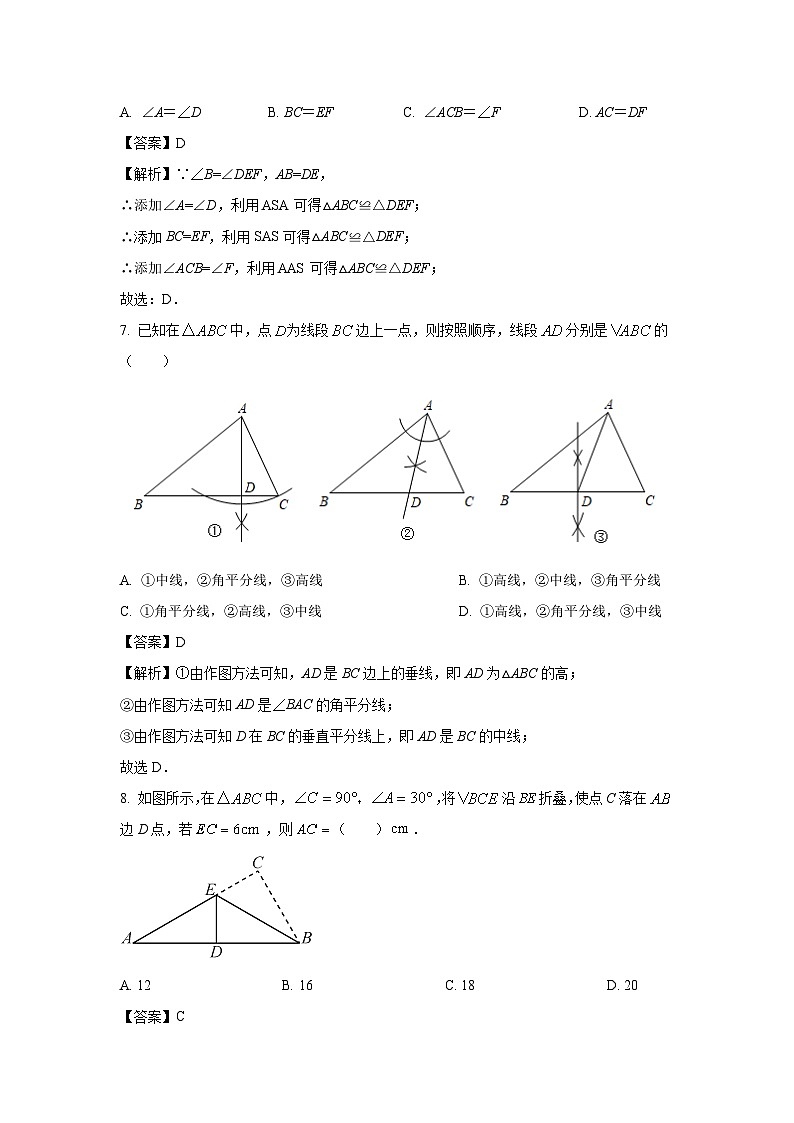
7. 已知在中,点为线段边上一点,则按照顺序,线段分别是的( )
A. ①中线,②角平分线,③高线B. ①高线,②中线,③角平分线
C. ①角平分线,②高线,③中线D. ①高线,②角平分线,③中线
【答案】D
【解析】①由作图方法可知,AD是BC边上的垂线,即AD为△ABC的高;
②由作图方法可知AD是∠BAC的角平分线;
③由作图方法可知D在BC的垂直平分线上,即AD是BC的中线;
故选D.
8. 如图所示,在中,,将沿折叠,使点C落在边D点,若,则( ).
A. 12B. 16C. 18D. 20
【答案】C
【解析】根据折叠的性质,
∴,
∵,
∴,
∴,
故选C.
9. 如图所示,将正方形纸片三次对折后,沿图中AB线剪掉一个等腰直角三角形,展开铺平得到的图形是( )
A. B. C. D.
【答案】A
【解析】找一张正方形的纸片,按上述顺序折叠、裁剪,然后展开后得到的图形如图所示:
故选A.
10. 若一个多边形的内角和为1080°,则这个多边形的边数为( )
A. 6B. 7C. 8D. 9
【答案】C
【解析】设这个多边形的边数为n,由n边形的内角和等于180°(n﹣2),
可得方程180°(n﹣2)=1080°,
解得:n=8.
故选C.
11. 如图,在中,已知点D、E、F分别为边、、的中点,且的面积是,则阴影部分面积等于( )
A. B. C. D.
【答案】C
【解析】点F是的中点,
∴的底是,的底是,即=,而高相等,
∴.
∵E是的中点,
∴,,
∴
∴.
∵,
∴,
即阴影部分的面积为.
故选:B.
12. 如图,在平面直角坐标系中xOy中,已知点A的坐标是(0,2),以OA为边在右侧作等边三角形OAA1,过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2,再过点A2作x轴的垂线,垂足为点O2,以O2A2为边在右侧作等边三角形O2A2A3,……,按此规律继续作下去,得到等边三角形O2020A2020A2021,则点A2023的纵坐标为( )
A. ()2021B. ()2022C. ()2023D. ()2024
【答案】B
【解析】∵三角形OAA1是等边三角形,
∴OA1=OA=2,∠AOA1=60°,
∴∠O1OA1=30°.
在直角△O1OA1中,∵∠OO1A1=90°,∠O1OA1=30°,
∴O1A1=OA1=1,即点A1的纵坐标为1,
同理,O2A2=O1A2=()1,O3A3=O2A3=()2,
即点A2的纵坐标为()1,
点A3的纵坐标为()2,
…
∴点A2023的纵坐标为()2022.
故选:B.
二、认真填一填,试一试自己的身手!本大题共6小题,每小题3分,共18分.只要求填写最后结果,请把答案填写在答案卷中横线上.
13. 如图,∠MON=35°,点P在射线ON上,以P为圆心,PO为半径画圆弧,交OM于点Q,连接PQ,则∠QPN=______.
【答案】70°
【解析】由作图可知,PO=PQ,
∴∠PQO=∠O=35°,
∴∠QPN=∠O+∠PQO=70°,
故答案为:70°.
14. 点关于直线的对称点的坐标是________.
【答案】
【解析】∵点横坐标为,
∴点P关于直线对称的点的横坐标为:7,
∴点关于直线对称点的坐标为:.
故答案为:.
15. 是的中线,和的周长的差是____.
【答案】2
【解析】∵是的中线,
∴,
∴和的周长的差,
∵,
∴和的周长的差.
故答案为:2.
16. 如图是两个全等三角形,图中的字母表示三角形的边长,则_____度.
【答案】54
【解析】∵两个三角形全等,
∴,
故答案为:54.
17. 等腰三角形一腰上的高与另一腰的夹角为,那么这个等腰三角形的顶角的度数为_______.
【答案】或
【解析】根据题意得:,
如图(1)所示,,则,即顶角为;
如图(2)所示,,则,
,
即顶角为;
故答案为:或.
18. 如图,为等边三角形,点分别在边上,与相交于点,且.则________度.
【答案】
【解析】∵是等边三角形,
∴,,
在和中,,
∴,
∴,
∴,
故答案为:.
三、专心解一解(本大题共8小题,满分66分)请认真读题,冷静思考.解答题应写出文字说明、证明过程或演算步骤.
19. 如图,点,,,一条直线上,,,,试说明:.
证明:,
,
,,
,
,
,
即:.
20. 如图,在平面直角坐标系中,点,,.
(1)在图中画出关于轴对称的,并直接写出点和点的坐标;
(2)在轴上画出点,使得的值最小(保留作图痕迹).
解:(1)如图,为所求,,;
(2)如图,点为所作.
21. 如图,已知∠A=∠D,AB=DB,点E在AC边上,∠AED=∠CBE,AB和DE相交于点F.
(1)求证:△ABC≌△DBE.
(2)若∠CBE=50°,求∠BED的度数.
证明:(1)∵∠A=∠D,∠AFE=∠BFD,
∴∠ABD=∠AED,
又∵∠AED=∠CBE,
∴∠ABD+∠ABE=∠CBE+∠ABE,
即∠ABC=∠DBE,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(ASA);
(2)解:∵△ABC≌△DBE,
∴BE=BC,
∴∠BEC=∠C,
∵∠CBE=50°,
∴∠BEC=∠C=65°.
22. 如图,在等边△ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=3,求DF的长.
解:(1)∵△ABC是等边三角形
∴∠B=60°
∵DE∥AB
∴∠EDC=∠B=60°
∵EF⊥DE
∴∠DEF=90°
∴∠F=90°﹣∠EDC=30°
(2)∵∠ACB=60°,∠EDC=60°
∴∠DEC=60°
∴△EDC是等边三角形
∵CD=3
∴ED=CD=3
∵∠DEF=90°,∠F=30°
∴DF=2ED=6
23. 如图,点E在上,,且,连接并延长,交的延长线于点F.
(1)求证:;
(2)若,,求的度数.
证明:(1)∵,
∴,
在和中,
,
∴,
∴;
(2),
∴,
∵,
∴,
∵
∴,
∵,
∴,
∴.
24. 如图,已知点D,E分别是的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.
(1)求证:是等腰三角形
(2)作∠ACE的平分线交AF于点G,若,求∠AGC的度数.
证明:(1)∵AF是∠DAC的角平分线
∴∠DAF=∠CAF
又∵
∴∠DAF=∠ABC,∠CAG=∠ACB
∴∠ABC=∠ACB
∴AB=AC
∴是等腰三角形
(2)∵CG是∠ACE的角平分线
∴∠ACG=∠ECG
又∵,∠ACB=∠B
∴
∴∠ACG=∠ECG=
又∵∠CAG=∠ACB
∴∠AGC=
25. 如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形特异线,称这个三角形为特异三角形.
(1)如图1,是等腰锐角三角形,,若的角平分线交于点,且是的一条特异线,则______;
(2)如图2,中,,线段的垂直平分线交于点,交于点.求证:是的一条特异线.
解:(1)是一条特异线,
,是等腰三角形,
,
,
的角平分线是,
,
是等腰锐角三角形,
,
内角和为,
.
(2)垂直平分线,
,
是等腰三角形,
,
,
,
,
,
是等腰三角形,
是的一条特异线.
26. 已知,点,分别为线段,上两点,连接,交于点.
图1 图2
(1)若,,如图1所示,______;
(2)若平分,平分,如图2所示,试说明此时与的数量关系;
(3)在(2)的条件下,若,试说明:.
解:(1)∵,,
∴,,
∴,
即:,
故答案为:
(2)∵平分,平分,
∴,,
∵,
即:
∴;
(3)如图,作的平分线交于点,
∵,
∴,
∴,
又∵平分,
∴,
在和中,
,
∴,
∴,
在和中,
,
∴,
∴,
即:.
相关试卷
这是一份2023-2024学年山东省济宁市梁山县九年级(上)期中数学试卷(解析版),共16页。试卷主要包含了请将答案正确填写在答题卡上等内容,欢迎下载使用。
这是一份2023-2024学年山东省济宁市梁山县七年级(上)期末数学试卷(含详细答案解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年山东省济宁市梁山县七年级(上)期末数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









