2023~2024学年山东省临沂市费县九年级(上)期中数学试卷(解析版)

这是一份2023~2024学年山东省临沂市费县九年级(上)期中数学试卷(解析版)，共12页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
第Ⅰ卷（选择题 共48分）
一、选择题（本大题共12小题，每小题4分，共48分）请将唯一正确答案的代号填涂在答题卡上．
1. 将一元二次方程化成一般形式后，二次项系数和一次项系数分别是（ ）
A. 2， B. 2，0C. 2，3D. 2，
【答案】D
【解析】将一元二次方程化成一般形式是，
∴二次项的系数和一次项系数分别是2和，
故选：D．
2. 下列图形中，是中心对称图形的是（ ）
A. B.
C. D.
【答案】A
【解析】选项B、C、D均不能找到这样的一个点，使图形绕某一点旋转后与原来的图形重合，所以不是中心对称图形；
选项A能找到这样的一个点，使图形绕某一点旋转后与原来的图形重合，所以是中心对称图形；
故选：A．
3. 用配方法解一元二次方程x2+4x﹣1＝0，配方后得到的方程是（ ）
A （x﹣1）2＝5B. （x+2）2＝5
C. （x+1）2＝5D. （x+2）2＝3
【答案】B
【解析】x2+4x﹣1＝0，
移项得：x2+4x=1，
配方得：x2+4x+4=1+4，即（x+2）2=5，
故选：B．
4. 对于抛物线,下列结论：①抛物线的开口向下；②对称轴为直线；③顶点坐标为;④时,随的增大而减小．其中正确结论的个数为（ ）
A. 1B. 2C. 3D. 4
【答案】C
【解析】∵a＝−＜0，
∴抛物线开口方向向下，故①正确；
对称轴为直线x＝−2，故②错误；
顶点坐标为（−2，−5），故③正确；
∵x＞−2时，y随x的增大而减小，
∴x＞2时，y随x的增大而减小，故④正确；
综上所述，正确结论有①③④共3个．
故选：C．
5. 如图，四边形内接于，若，则的度数为（ ）
A. B. C. D.
【答案】B
【解析】∵四边形内接于，
∴，而，
∴，
∴．
故选：B．
6. 将抛物线y＝2（x﹣1）2﹣3向右移动2个单位，再向下移动3个单位，得到的抛物线的解析式为（ ）
A. y＝2（x+1）2B. y＝2（x+1）2﹣6
C. y＝2（x﹣3）2D. y＝2（x﹣3）2﹣6
【答案】D
【解析】把抛物线y＝2(x-1)2-3向右平移2个单位，再向下平移3个单位，则所得抛物线的解析式是 y＝2(x-1-2)2-3-3，即y＝2(x-3)2-6，
故选D．
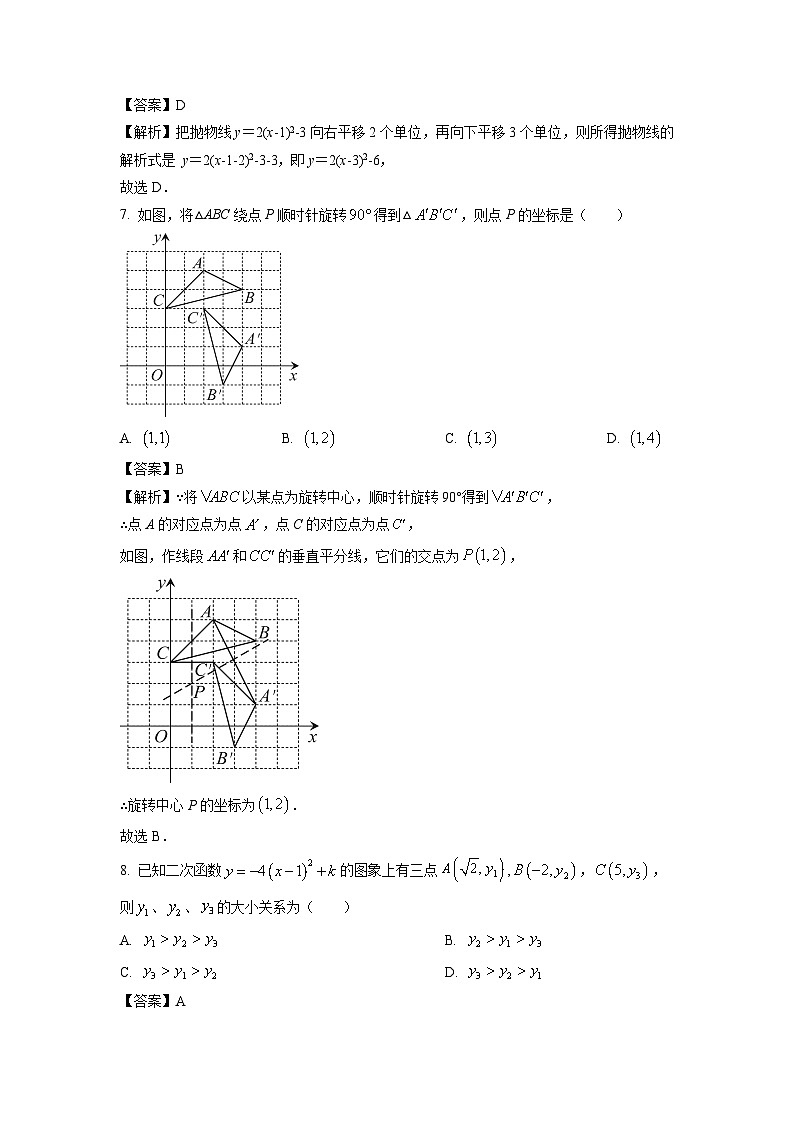
7. 如图，将△ABC绕点P顺时针旋转得到△，则点P的坐标是（ ）
A. B. C. D.
【答案】B
【解析】∵将以某点为旋转中心，顺时针旋转90°得到，
∴点A的对应点为点，点C的对应点为点，
如图，作线段和的垂直平分线，它们的交点为，
∴旋转中心P的坐标为．
故选B．
8. 已知二次函数的图象上有三点,，，则、、的大小关系为（ ）
A. B.
C. D.
【答案】A
【解析】
A、故选项正确，符合题意；
B、故选项错误，不符合题意；
C、故选项错误，不符合题意；
D、故选项错误，不符合题意．
故选：A．
9. 如图，⊙O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段OM的长的取值范围是（ ）
A.
B.
C.
D.
【答案】B
【解析】如图，连接OA，作OM⊥AB于M，
∵⊙O的直径为10，
∴半径为5，
∴OM的最大值为5，
∵OM⊥AB于M，
∴AM=BM，
∵AB=6，
∴AM=3，
在Rt△AOM中，；
此时OM最短，
所以OM长的取值范围是4≤OM≤5．
故选：B．
10. 如图，在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分) ，余下部分种植草坪，要使草坪的面积为540平方米，则设道路的宽为xm，根据题意，列方程( ) .

A.
B.
C.
D.
【答案】C
【解析】设道路的宽为x，根据题意得（32-x）（20-x）=540．
故选C．
11. 已知抛物线y＝ax2+bx+c（a＞0）与x轴分别交于（﹣1，0），（5，0）两点，当自变量x＝1时，函数值为y1；当x＝3，函数值为y2．下列结论正确的是（ ）
A. y1＞y2B. y1＝y2C. y1＜y2D. 不能确定
【答案】B
【解析】由抛物线与x轴交点坐标可知，对称轴是直线，
∵x＝1，x＝3对应的两点也关于直线x＝2对称，∴函数值也相等．
故选B．
12. 如图所示，已知二次函数的图象与轴交于、两点，与轴交于点．对称轴为直线．直线与抛物线交于、两点，点在轴下方且横坐标小于3，则下列结论：①；②；③；④．其中正确的有（ ）
A. 4个B. 3个C. 2个D. 1个
【答案】C
【解析】∵抛物线与y轴的交点在x轴上方，
∴，
∵抛物线的对称轴为直线，
∴，
∴，所以①正确；
∵抛物线与x轴的一个交点在点左侧，
而抛物线的对称轴为直线，
∴抛物线与x轴的另一个交点在点右侧，
∴当时，，
∴，所以②正确；
∵时，二次函数有最大值,
∴，
∴，所以③正确；
∵直线与抛物线交于C、D两点,D点在x轴下方且横坐标小于3，
∴时，一次函数值比二次函数值大，
即，
而，
∴，解得，所以④正确，
故选A．
第Ⅱ卷（非选择题 共72分）
二、填空题（本大题共4小题，每小题4分，共16分）
13. 已知，是一元二次方程的两个实数根，则的值为______．
【答案】5
【解析】∵a，b是一元二次方程的两个实数根，
∴
．
故答案为：5．
14. 把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4cm，则球的半径为____cm．
【答案】2.5
【解析】EF的中点M，作MN⊥AD于点M，取MN上的球心O，连接OF，
设OF=x，则OM=4−x，MF=2，
在中，
即：
解得：x=2.5，
故答案为2.5．
15. 如图,在同一平面内,将△ABC绕点A逆时针旋转40°到△AED的位置,恰好使得DC∥AB,则∠CAB的大小为______________.
【答案】70°
【解析】由旋转的性质可知：∠CAD=40°，AD=AC，
∴∠ACD=∠ADC=，
∵CD∥AB，
∴∠CAB=∠ACD=70°.
故答案为70°.
16. 如图，AB是⊙O的直径，C、D是⊙O上的点，且OC∥BD，AD分别与BC、OC相较于点E、F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD；④△CEF≌△BED．其中一定成立的是_____（把你认为正确结论的序号都填上）．
【答案】①③
【解析】①、∵AB是⊙O的直径，
∴∠ADB=90°，
∴AD⊥BD，
②、∵∠AOC是⊙O的圆心角，∠AEC是⊙O的圆内部的角，
∴∠AOC≠∠AEC，
③、∵OC∥BD，
∴∠OCB=∠DBC，
∵OC=OB，
∴∠OCB=∠OBC，
∴∠OBC=∠DBC，
∴BC平分∠ABD，
④、∵△CEF和△BED中，没有相等的边，
∴△CEF与△BED不全等，
故答案为①③
三、解答题（本大题共5小题，共56分．解答应写出文字说明、证明过程或演算步骤）
17. 用适当的方法解下列方程：
（1）
（2）；
解：（1）
，
即：，；
（2）
，
即：，，
则有：，．
18. 如图，四边形ABCD是正方形．△ABE是等边三角形，M为对角线 BD(不含B，D点)上任意一点，将线段BM绕点B逆时针旋转60°得到BN，连接 EN，AM、CM．请判断线段 AM 和线段 EN 的数量关系，并说明理由．
解：AM=EN，理由为：
∵△ABE是等边三角形，∴AB=BE，∠ABE=60°，即∠EBN=∠ABN=60°，
∵线段BM绕点B逆时针旋转60°得到BN，∴BM=BN，∠MBN=60°，
即∠ABM+∠ABN=60°，∴∠ABM=∠EBN，
在△ABM和△EBN中，，∴△ABM≌△EBN（SAS），∴AM=EN．
19. 如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m2？
解：设矩形猪舍垂直于住房墙一边长为xm，可以得出平行于墙的 一边的长为m，
由题意得 ，
化简，得，解得：，
当时，（舍去），
当时，，
答：所围矩形猪舍的长为10m、宽为8m．
20. 某玩具厂计划生产一种玩具，每日最高产量为40只，且每日产出的产品全部售出．已知生产只玩具的成本为（元），售价每只为（元），且、与的关系式分别为，．
（1）当日产量为多少时，每日获得的利润为1750元?
（2）当日产量为多少时，可获得最大利润?最大利润是多少?
解：（1）由题意得：，
解得：（大于每日最高产量为40只，故舍去）
答：当日产量为25只时，每日获得的利润为1750元．
（2）设每天所获利润为W．
由题意得，
∴当时，W有最大值1950元．
答：当日产量为35只时，可获得最大利润，最大利润为1950元．
21. 已知抛物线经过，，三点，对称轴是直线．关于的方程有两个相等的实数根．
（1）求抛物线的解析式；
（2）若，试比较与的大小；
（3）若，两点在直线的两侧，且，求的取值范围．
解：（1）抛物线经过，①，
对称轴是直线，②，
关于的方程有两个相等的实数根，
③，
由①②③可得：，
抛物线的解析式为；
（2），
，
点，点在对称轴直线的右侧，
抛物线，
，即在对称轴的右侧随的增大而减小，
，
，
；
（3）若点在对称轴直线的左侧，点在对称轴直线的右侧时，
由题意可得，
，
若点在对称轴直线的左侧，点在对称轴直线的右侧时，
由题意可得：，
不等式组无解，
综上所述：．