北师大版（2024）八年级下册6 一元一次不等式组精品练习题

这是一份北师大版（2024）八年级下册6 一元一次不等式组精品练习题，文件包含北师大版数学八下同步讲练第二章第03讲一元一次不等式组8类热点题型讲练原卷版docx、北师大版数学八下同步讲练第二章第03讲一元一次不等式组8类热点题型讲练解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。
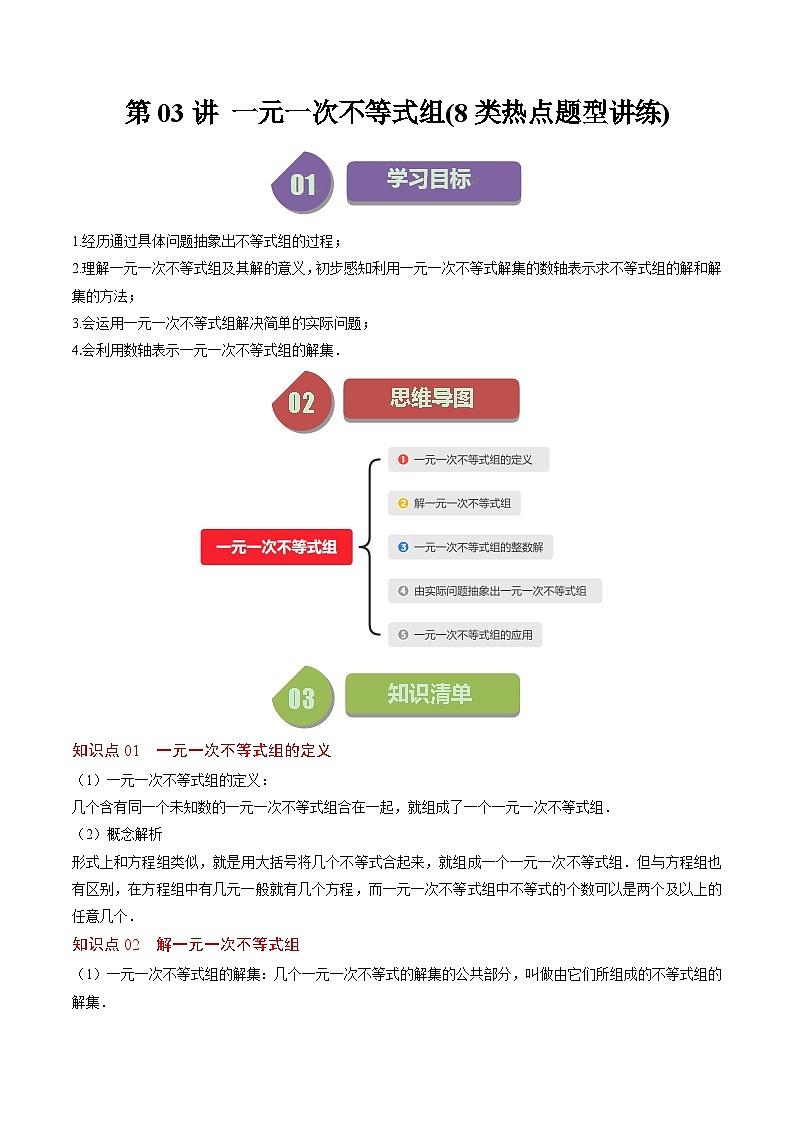
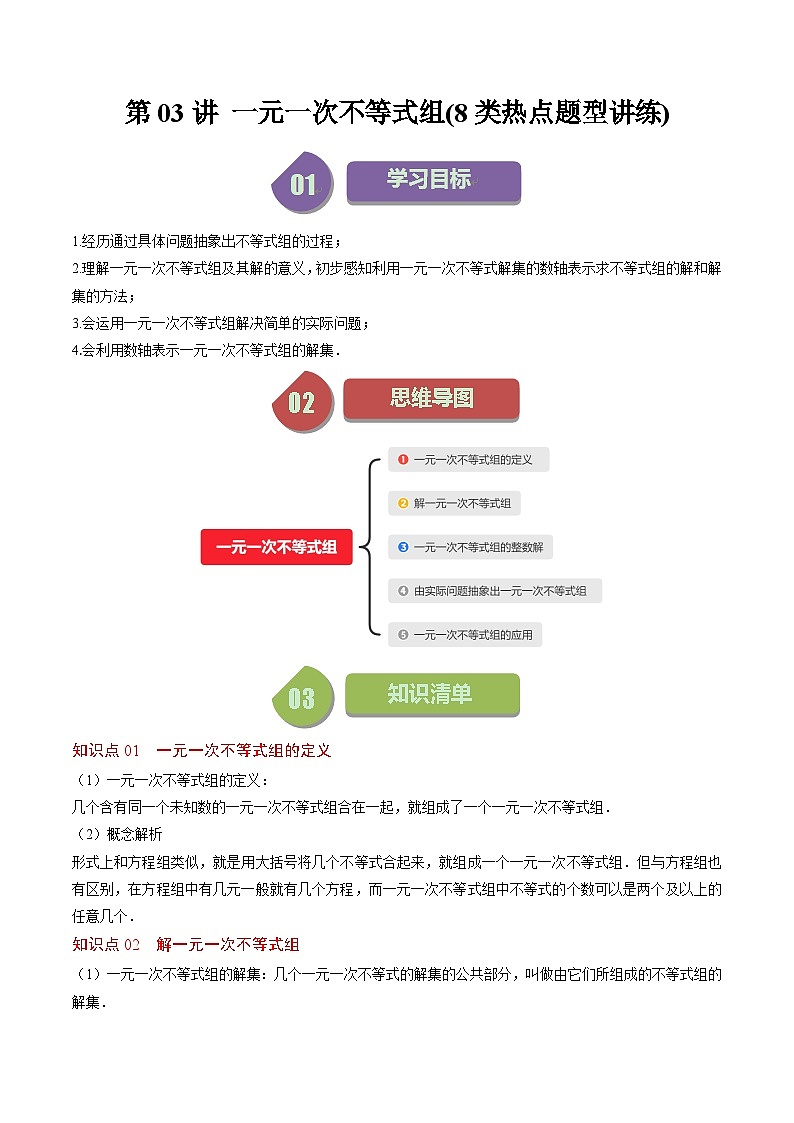
2.理解一元一次不等式组及其解的意义，初步感知利用一元一次不等式解集的数轴表示求不等式组的解和解集的方法；
3.会运用一元一次不等式组解决简单的实际问题；
4.会利用数轴表示一元一次不等式组的解集．
知识点01 一元一次不等式组的定义
（1）一元一次不等式组的定义：
几个含有同一个未知数的一元一次不等式组合在一起，就组成了一个一元一次不等式组．
（2）概念解析
形式上和方程组类似，就是用大括号将几个不等式合起来，就组成一个一元一次不等式组．但与方程组也有区别，在方程组中有几元一般就有几个方程，而一元一次不等式组中不等式的个数可以是两个及以上的任意几个．
知识点02 解一元一次不等式组
（1）一元一次不等式组的解集：几个一元一次不等式的解集的公共部分，叫做由它们所组成的不等式组的解集．
（2）解不等式组：求不等式组的解集的过程叫解不等式组．
（3）一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．
方法与步骤：①求不等式组中每个不等式的解集；②利用数轴求公共部分．
解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
知识点03 一元一次不等式组的整数解
（1）利用数轴确定不等式组的解（整数解）．
解决此类问题的关键在于正确解得不等式组或不等式的解集，然后再根据题目中对于解集的限制得到下一步所需要的条件，再根据得到的条件进而求得不等式组的整数解．
（2）已知解集（整数解）求字母的取值．
一般思路为：先把题目中除未知数外的字母当做常数看待解不等式组或方程组等，然后再根据题目中对结果的限制的条件得到有关字母的代数式，最后解代数式即可得到答案．
知识点04 由实际问题抽象出一元一次不等式组
由实际问题列一元一次不等式组时，首先把题意弄明白，在此基础上找准题干中体现不等关系的语句，根据语句列出不等关系．往往不等关系出现在“不足”，“不少于”，“不大于”，“不超过”等这些词语出现的地方．所以重点理解这些地方有利于自己解决此类题目．
知识点05 一元一次不等式组的应用
对具有多种不等关系的问题，考虑列一元一次不等式组，并求解．
一元一次不等式组的应用主要是列一元一次不等式组解应用题，其一般步骤：
（1）分析题意，找出不等关系；
（2）设未知数，列出不等式组；
（3）解不等式组；
（4）从不等式组解集中找出符合题意的答案；
（5）作答．
题型01 一元一次不等式组的定义
【例题】（2023上·广东梅州·九年级校考开学考试）下列不等式组为一元一次不等式组的是（ ）
A． B． C． D．
【变式训练】
1．（2023下·七年级课时练习）下列选项中，是一元一次不等式组的是（ ）
A． B． C． D．
2．（2023上·浙江·八年级专题练习）下列不等式组：①；②；③；④；⑤，其中是一元一次不等式组的个数（ ）
A．2个B．3个C．4个D．5个
题型02 求一元一次不等式组的解集
【例题】（2023下·江苏·七年级专题练习）解不等式组，并在数轴上画出它的解集．
【变式训练】
1．（2023上·江苏苏州·七年级校联考阶段练习）解不等式，并把它的解集在数轴上表示出来．
2．（2023上·湖南株洲·八年级校考阶段练习）解不等式组，并在数轴上表示出解集：
(1)； (2)．
题型03 求一元一次不等式组的整数解
【例题】（2023上·浙江·八年级专题练习）不等式组的整数解为 ．
【变式训练】
1．（2023下·安徽宿州·八年级校考期中）不等式组的所有整数解的和是 ．
2．（2023下·四川宜宾·七年级统考期末）以不等式组的整数解为边长的等腰三角形的周长是 ．
题型04 解一元一次不等式组中错解复原问题
【例题】（2023下·河南开封·七年级统考期末）下面是小李同学解不等式组的过程，请认真阅读并完成相应任务．
解：令
解不等式①，
去分母，得 第一步
移项，得 第二步
合并同类项，得 第三步
系数化为1，得 第四步
任务一：
上述解不等式①的过程第______步出现了错误，其原因是______．
任务二：
请写出正确的解题过程，并将不等式组的解集在数轴上表示出来，
【变式训练】
1．（2023下·贵州安顺·七年级统考期末）请观察框内小明同学解不等式的过程，回答下列问题：
(1)第______步出现错误；
(2)该不等式的正确解集为：______；
(3)要使不等式组的解集包含3个整数解，则在括号里添加的一元一次不等式可以为：______，此不等式组的解集是：______．
2．（2023下·宁夏中卫·八年级统考期末）下面是小明同学解不等式组的过程，请认真阅读，完成相应的任务．
解：由不等式，得，第一步
解得，第二步
由不等式，得，第三步
移项，得，第四步
解得，第五步
所以，原不等式组的解集是．第六步
任务一：

(1)小明的解答过程中，第______步开始出现错误，错误的原因是______________________________；
任务二：
(2)这个不等式组正确的解集是____________（直接写出），并在数轴上表示出来．
题型05 由一元一次不等式组的解集求参数
【例题】（2023上·江苏南通·九年级校考期末）若关于不等式组若无解，则的取值范围 ．
【变式训练】
1．（2023·广东河源·一模）若关于x的不等式组的解集是，则a的取值范围是 ．
2．（2023下·江苏苏州·七年级统考期末）关于x的不等式组恰有四个整数解，那么m的取值范围为 ．
题型06 一元一次不等式组和方程组结合的问题
【例题】（2023下·福建泉州·七年级福建省泉州市培元中学校考期中）已知关于，的方程组的解均是负数．
(1)求的取值范围；
(2)若，求的取值范围．
【变式训练】
1．（2023上·江苏淮安·八年级淮安市浦东实验中学校考开学考试）若关于，的二元一次方程的解满足，求的取值范围．
2．（2023下·湖北恩施·七年级校考阶段练习）已知关于x、y的方程组的解x为负数，y为非正数．
(1)求a的取值范围；
(2)在a的取值范围内，当a取何整数时，不等式的解为？
题型07 列一元一次不等式组
【例题】（2023下·四川达州·八年级校考期中）八年级某班级部分同学去植树，若每人平均植树 8 棵，还剩 7 棵，若每人平均植树 9 棵，则有 1 位同学植树的棵数不到 8 棵．若设同学人数为 x 人，则下列各项能准确的求出同学人数与种植的树木的数量的是( )
A． B．
C．D．
【变式训练】
1．（2023·全国·七年级假期作业）一本书共98页，张力读了一周(7天)还没读完，而李永不到一周就已读完．李永平均每天比张力多读3页．若设张力平均每天读x页，则由题意列出不等式组为( )
A．B．
C．D．
2．（2023下·江苏无锡·七年级无锡市天一实验学校校考阶段练习）若一艘轮船沿江水顺流航行用时少于小时，它沿江水逆流航行也用时少于小时，设这艘轮船在静水中的航速为，江水的流速为，则根据题意可列不等式组为（ ）
A．B．
C．D．
题型08 一元一次不等组的应用
【例题】（2023上·浙江宁波·八年级统考期末）在我市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元．
(1)求每台电脑、每台电子白板各多少万元？
(2)根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，该校有几种购买方案？
(3)上面的哪种方案费用最低？按费用最低方案购买需要多少钱？
【变式训练】
1．（2023上·重庆沙坪坝·八年级重庆一中校考期末）大华橱具店购进电饭煲和电压锅两种电器进行销售，其进价与售价如表：
(1)一季度，橱具店购进这两种电器共30台，用去了5600元，并且全部售完，问橱具店在该买卖中赚了多少钱？
(2)为了满足市场需求，二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台，且电饭煲的数量不少于电压锅的，问橱具店有哪几种进货方案？并说明理由；
(3)在（2）的条件下，请你通过计算判断，哪种进货方案橱具店赚钱最多？
2．（2023上·吉林白山·七年级统考期末）甲、乙两所幼儿园计划在“元旦”一起举办文艺汇演活动，已知甲、乙两所幼儿园一共96人（其中甲幼儿园人数多于乙幼儿园人数，且甲幼儿园人数不足90人）．现准备给每位小朋友都购买一套演出服装，服装厂给出如下价目表：
如果两所幼儿园分别单独购买服装，一共应付5680元．
(1)如果甲、乙两所幼儿园联合起来购买服装，那么比各自购买服装共可以节省多少钱？
(2)甲、乙两所幼儿园各有多少名小朋友准备参加演出？
(3)如果甲幼儿园有10名小朋友因为校外活动不能参加演出，那么你有几种购买方案？通过比较，你认为如何购买服装才能最省钱？
一、单选题
1．（2023下·七年级单元测试）下列不等式组是一元一次不等式组的是（ ）
A．B．C．D．
2．（2023上·浙江·八年级统考阶段练习）不等式组的解集是（ ）
A．B．C．D．
3．（2023下·全国·八年级假期作业）满足不等式组的整数解有（ ）
A．6个B．4个C．5个D．无数个
4．（2023下·黑龙江哈尔滨·七年级统考期末）在平面直角坐标系中，在第二象限，则m的取值范围是（ ）
A．B．C．D．
5．（2023上·湖南永州·八年级校考阶段练习）已知关于x的不等式组有两个整数解，则a的取值范围为（ ）
A．B．C．D．
二、填空题
6．（2023·福建莆田·校考模拟预测）不等式组的正整数解是 ．
7．（2023上·浙江金华·九年级校考阶段练习）若不等式组无解，则的取值范围是 ．
8．（2023上·河南濮阳·九年级统考期中）已知关于x、y的方程组的解是正数，则a的取值范围是 ．
9．（2023下·八年级课时练习）把一筐梨分给几个学生，若每人4个，则剩下3个；若每人6个，则最后一个同学最多分得3个，求学生人数和梨的个数．设有a个学生，依题意可列不等式组为 ．
10．（2023上·重庆沙坪坝·八年级统考期中）若关于的不等式组的解集为，且关于的方程的解是非负整数，则所有满足条件的整数的值之和是 ．
三、解答题
11．（2023上·浙江·八年级期末）解不等式组，并写出它所有的整数解．
12．（2023上·江苏苏州·七年级校考阶段练习）求不等式组的解集，并把解集在数轴上表示出来，写出它的所有非负整数解．
13．（2023上·浙江·八年级校联考期末）解不等式组
下面是某同学的部分解答过程，请认真阅读并完成任务：
解：解不等式①，得 第1步
合并同类项，得 第2步
两边都除以，得 第3步
任务一：该同学的解答过程中第 步出现了错误，这一步的依据是 ，不等式①的正确解是 ．
任务二：解不等式②，并写出该不等式组的解集．
14．（2023下·七年级课时练习）有学生若干人，住若干间宿舍．若每间住4人，则有20人无法安排住宿；若每间住8人，则有一间宿舍不满也不空，问宿舍间数是多少？
15．（2023下·黑龙江牡丹江·七年级统考期末）已知关于，的方程组，其中为非负数，为正数，求的整数解．
16．（2023下·湖北武汉·七年级校考阶段练习）已知关于x，y的方程组的解都为非负数．
(1)求a的取值范围；
(2)若，求的取值范围．
17．（2023下·江苏·七年级专题练习）接种新冠病毒疫苗，建立全民免疫屏障，是战胜病毒的重要手段．北京科兴中维需运输一批疫苗到我市疾控中心，据调查得知，2辆A型冷链运输车与3辆B型冷链运输车一次可以运输600盒；5辆A型冷链运输车与6辆B型冷链运输车一次可以运输1350盒．
(1)求每辆A型车和每辆B型车一次可以分别运输多少盒疫苗．
(2)计划用两种冷链运输车共12辆运输这批疫苗，A型车一次需费用5000元，B型车一次需费用3000元．若运输物资不少于1500盒，且总费用小于54000元．请你列出所有运输方案，并指出哪种方案所需费用最少，最少费用是多少？
18．（2023下·福建泉州·七年级统考期中）我们约定一种新运算，规定：（其中a、b均为非零常数），这里等式右边是通常的四则运算，例如：．
(1)若，．
①求常数a、b的值；
②若关于m的不等式组无解，求有理数p的取值范围；
(2)非零常数a、b应满足什么条件时，才能使对于任意有理数t都成立？请写出推理过程．
解不等式
解：…………第一步
……………………第二步
……………………第三步
………………………………第四步
……………………………………第五步
进价（元/台）
售价（元/台）
电饭煲
200
250
电压锅
160
200
购买服装的套数
48套以下
48套至90套
91套及以上
每套服装的价格
65元
55元
45元