


所属成套资源:人教版数学九上同步讲练 (2份,原卷版+解析版)
人教版(2024)九年级上册24.3 正多边形和圆精品同步测试题
展开
这是一份人教版(2024)九年级上册24.3 正多边形和圆精品同步测试题,文件包含人教版数学九上同步讲练第24章第07讲正多边形与圆扇形的弧长与面积原卷版docx、人教版数学九上同步讲练第24章第07讲正多边形与圆扇形的弧长与面积解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
知识点01 正多边形与圆
正多边形的概念:
各条边 ,各个角也 的多边形叫做正多边。
圆的内接正多边形:
把一个圆 分成n(n是大于2的自然数)份,依次连接各 所得的多边形是这个圆
的 ,这个圆叫做这个正多边形的 。
圆的内接正多边形的相关概念:
(1)中心:正多边形的 的圆心叫做正多边形的中心。
即O既是圆心也是正多边形的中心。
(2)正多边形的半径: 的半径叫做正多边形的半径。
即OB既是圆的半径,也是正多边形的半径。
(3)中心角:正多边形每一边所对的 叫做正多边形
的中心角。正多边形的中心角度数为 。
即∠BOC是正多边形的一个中心角。
(4)边心距: 到正多边形的 的距离叫做正多边形的边心距。
即过O做边BC的垂线即为边心距。
题型考点:①概念的理解。②有关的计算。
【即学即练1】
1.下列说法不正确的是( )
A.圆内正n边形的中心角为
B.各边相等的,各角相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的多边形是正多边形
【即学即练2】
2.如图,五边形ABCDE是⊙O的内接正五边形,则正五边形中心角∠COD的度数是( )
A.60°B.36°C.76°D.72°
【即学即练3】
3.如图,在圆内接正六边形ABCDEF中,BF,BD分别交AC于点G,H.若该圆的半径为15厘米,则线段GH的长为( )
A.厘米B.5厘米C.3厘米D.10厘米
【即学即练4】
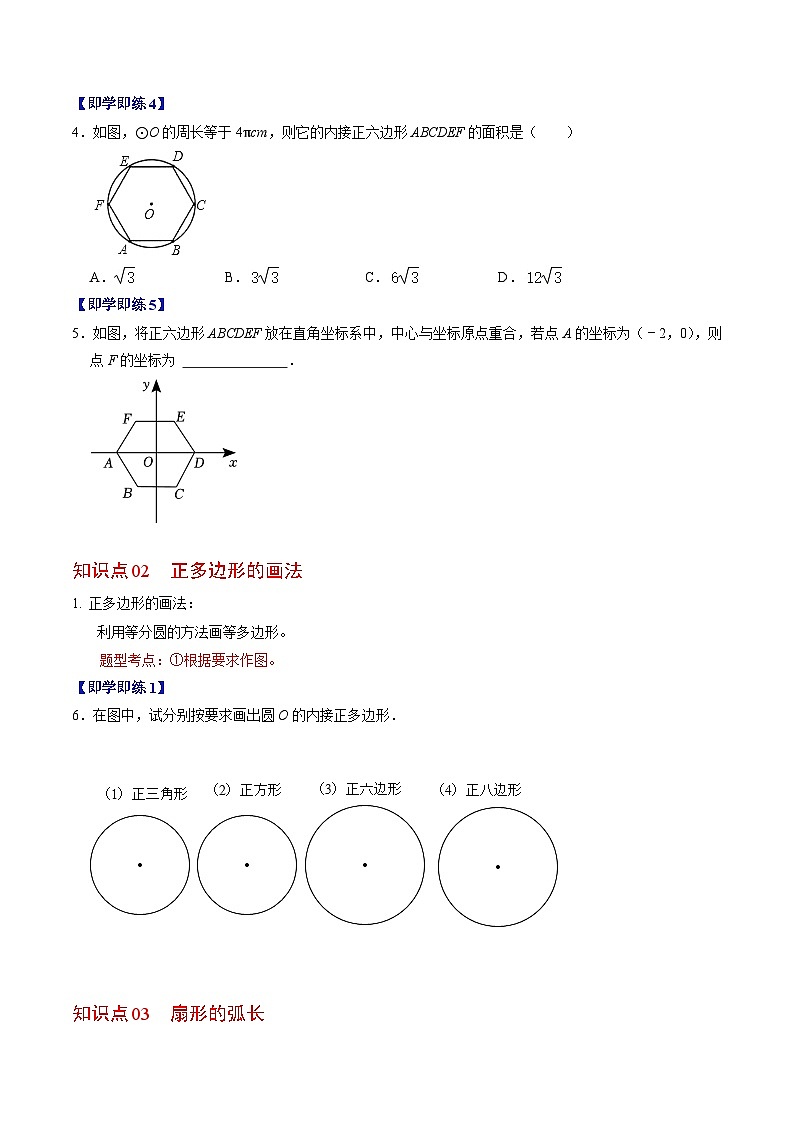
4.如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( )
A.B.C.D.
【即学即练5】
5.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若点A的坐标为(﹣2,0),则点F的坐标为 .
知识点02 正多边形的画法
正多边形的画法:
利用等分圆的方法画等多边形。
题型考点:①根据要求作图。
【即学即练1】
6.在图中,试分别按要求画出圆O的内接正多边形.
知识点03 扇形的弧长
扇形弧长的定义:
扇形的弧长就是扇形两条 间的 的长度。
扇形弧长的计算公式:
在半径为r的圆中,n°的圆心角所对的弧的长度为 。
题型考点:①弧长的计算。
【即学即练1】
7.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则的长为( )
A.6πB.2πC.πD.π
【即学即练2】
8.如图,扇形OAB中,OB=3,∠AOB=100°,点C在OB上,连接AC,点O关于AC的对称点D刚好落在上,则的长是( )
A.B.C.D.
知识点04 扇形的面积
扇形的面积计算公式:
方法1:已知扇形的圆心角为n°,半径为r,则扇形的面积为: 。
方法2:已知扇形的半径为r,弧长为l,则扇形的面积公式为: 。
题型考点:①扇形面积的计算。②面积公式的应用。
【即学即练1】
9.已知一个扇形的半径为6cm,圆心角为150°,则这个扇形的面积为 cm2.
【即学即练2】
10.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为 .
【即学即练3】
11.如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧,交AC于点E,若∠A=60°,∠ABC=100°,BC=4,则扇形BDE的面积为 .
【即学即练4】
12.扇形的弧长为20πcm,面积为240πcm2,则扇形的半径为 cm.
题型01 正多边形与圆的相关计算
【典例1】
如图,⊙O是正五边形ABCDE的外接圆,点P为ED上的一点,则∠APC的度数为 .
【典例2】
如图,在正五边形ABCDE中,连接AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是( )
A.18°B.30°C.36°D.40°
【典例3】
如图,正六边形ABCDEF的边长为2,则△ACE的周长为 .
【典例4】
如图,正六边形内接于⊙O中,已知外接圆的半径为2,则阴影部分面积为 .
题型02 扇形的弧长计算
【典例1】
若扇形的圆心角为90°,半径为6,则该扇形的弧长为 .
【典例2】
如图所示的正方形网格中,O,A,B,C,D是网格线交点,若与所在圆的圆心都为点O,则与的长度之比为 .
【典例3】
如图,王虎使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.10cmB.4πcmC.D.
【典例4】
一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD是水平的,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为 cm.
题型03 阴影部分的面积计算
【典例1】
如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置时,若AB=2,AD=4,则阴影部分的面积为( )
A.π﹣B.π﹣2C.π﹣4D.π﹣2
【典例2】
如图,正方形ABCD的边长为4,以BC为直径的半圆O交对角线BD于点E.则图中阴影部分的面积为( )
A.8﹣πB.4+πC.6﹣πD.3+π
【典例3】
如图,以矩形ABCD的对角线AC为直径画圆,点D、B在该圆上,再以点A为圆心,AB的长为半径画弧,交AC于点E.若AC=2,∠BAC=30°.则图中影部分的面积和为 (结果保留根号和π).
【典例4】
如图,在△ABC中,BC=4,以点A为圆心、2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是 (结果保留π).
1.若⊙O的内接正n边形的边长与⊙O的半径相等,则n的值为( )
A.4B.5C.6D.7
2.已知圆内接正六边形的半径为2,则该内接正六边形的边心距为( )
A.1B.2C.D.
3.如图,AB是⊙O的直径,C是⊙O上一点,AC=4,BC=3,CD平分∠ACB交⊙O于点D,则劣弧AD的长为( )
A.πB.πC.2πD.π
4.道路施工部门在铺设如图所示的管道时,需要先按照其中心线计算长度后再备料.图中的管道中心线的长为(单位:m)( )
A.B.C.D.
5.如图,将一个圆分成甲、乙、丙三个扇形,其圆心角度数之比为2:3:4.若圆的半径为3,则扇形乙的面积为( )
A.B.C.3πD.4π
6.如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为BD,则图中阴影部分的面积为( )
A.B.C.D.
7.如图,在边长为的正八边形ABCDEFGH中,已知I,J,K,L分别是边AH,BC,DE,FG上的动点,且满足IA=JC=KE=LG,则四边形IJKL面积的最大值为( )
A.B.C.D.
8.如图,在半径为6cm的⊙O中,点A是劣弧的中点,点D是优弧上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3cm;③扇形OCAB的面积为12π;④四边形ABOC是菱形.其中正确结论的序号是( )
A.①③B.①②③④C.②③④D.①③④
9.如图,在等边三角形ABC中,D为BC的中点,交AC于点E,若AB=2,则的长为 .
10.如图,C,D是以AB为直径的半圆上的两点,连接BC,CD,AC,BD,BC=CD,∠ACD=30°,AB=12,则图中阴影部分的面积为 .
11.如图,正五边形ABCDE的边长为4,以AB为边作等边△ABF,则图中阴影部分的面积为 .
12.以正五边形ABCDE的顶点C为旋转中心,按顺时针方向旋转,使得新五边形A'B'CD'E'的顶点D'落在直线BC上,则正五边形ABCDE旋转的度数至少为 °.
13.如图,AB是⊙O的直径,AB=6,AC是⊙O的弦,∠BAC=30°,延长AB到D,连接CD,AC=CD.
(1)求证:CD是⊙O的切线;
(2)以BC为边的圆内接正多边形的周长等于 .
14.如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E.
(1)求证:四边形ADOE是正方形;
(2)若AB=4cm,求劣弧的长.
15.如图,在正方形ABCD中有一点P,连接AP、BP,旋转△APB到△CEB的位置.
(1)若正方形的边长是8,PB=4.求阴影部分面积;
(2)若PB=4,PA=7,∠APB=135°,求PC的长.
课程标准
学习目标
①正多边形与圆的相关概念及其关系
②正多边形的画法
③扇形的弧长与面积的计算公式
理解正多边形与圆的相关概念。
理解并掌握正多边形的半径与边长,边心距,中心角之间关系。
学会利用等分圆的方法画正多边形。
掌握并利用扇形的周长与面积计算公式进行相应的计算。
相关试卷
这是一份初中数学人教版(2024)九年级上册第二十四章 圆24.3 正多边形和圆精品课时作业,文件包含人教版数学九年级上册同步讲义+练习第24章第07讲正多边形与圆扇形的弧长与面积原卷版docx、人教版数学九年级上册同步讲义+练习第24章第07讲正多边形与圆扇形的弧长与面积解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
这是一份初中数学浙教版(2024)九年级上册第3章 圆的基本性质3.8 弧长及扇形的面积练习题,共65页。
这是一份初中数学人教版(2024)九年级上册24.1.1 圆达标测试,共34页。试卷主要包含了5°,OB=2,则的长为,6m,DC=0,5m,则阴影部分的面积为,14×22=12等内容,欢迎下载使用。










