湖南省永州市宁远县明德湘南高级中学2024-2025学年高一上学期期中考试数学试卷

这是一份湖南省永州市宁远县明德湘南高级中学2024-2025学年高一上学期期中考试数学试卷，共8页。试卷主要包含了单选题，多选题，填空题等内容，欢迎下载使用。
1．判断下列元素的全体可以组成集合的是（ ）
①湖北省所有的好学校；②直角坐标系中横坐标与纵坐标互为相反数的点；
③n的近似值；④不大于5的自然数．
A．①②B．②③C．②④D．③④
2．若，则的值为（ ）
A．B．3C．D．7
3．集合P＝{3，4，5}，Q＝{6，7}，定义＝{（a，b）|a∈P，b∈Q}，则的真子集个数为（ ）
A．31B．63C．32D．64
4．设全集，集合，，则下面Venn图中阴影部分表示的集合是（ ）
A． B． C． D．
5．“”是“”的（ ）
A．充要条件B．充分不必要条件
C．必要不充分条件D．既不充分也不必要条件
6．以下六个写法中：①；② ；③；④ ；⑤；正确的个数有（ ）
A．个B．个C．个D．个
7．设全集，集合，，则集合（ ）
A．B．C．D．
8．设U＝{1，2，3，4}，A与B是U的两个子集，若A∩B＝{3，4}，则称（A，B）为一个“理想配集”，那么符合此条件的“理想配集”（规定：（A，B）与（B，A）是两个不同的“理想配集”）的个数是（ ）
A．7个B．8个C．9个D．10个
二、多选题（每题6分，共18分）
9．（多选）下列各组中M、P表示不同集合的是（ ）
A．， B．
C．，
D．，
10．（多选）已知集合，集合⊆，则集合可以是（ ）
A． B． C． D．
11．函数是定义在R上的奇函数，下列说法正确的是（ ）
A．
B．若在上有最小值，则在上有最大值1
C．若在上为增函数，则在上为减函数
D．若时，，则时，
三、填空题（每题8分，共12分）
12．已知集合，且，则实数的值为___________.
13．已知，，，，则实数_____，____，_____．
三、解答题
15．已知，．
(1)当时，求；
(2)若，求实数m的取值范围．
16．已知集合.
(1)若A是空集，求的取值范围；
(2)若A中只有一个元素，求的值，并求集合A；
(3)若A中至少有一个元素，求的取值范围.
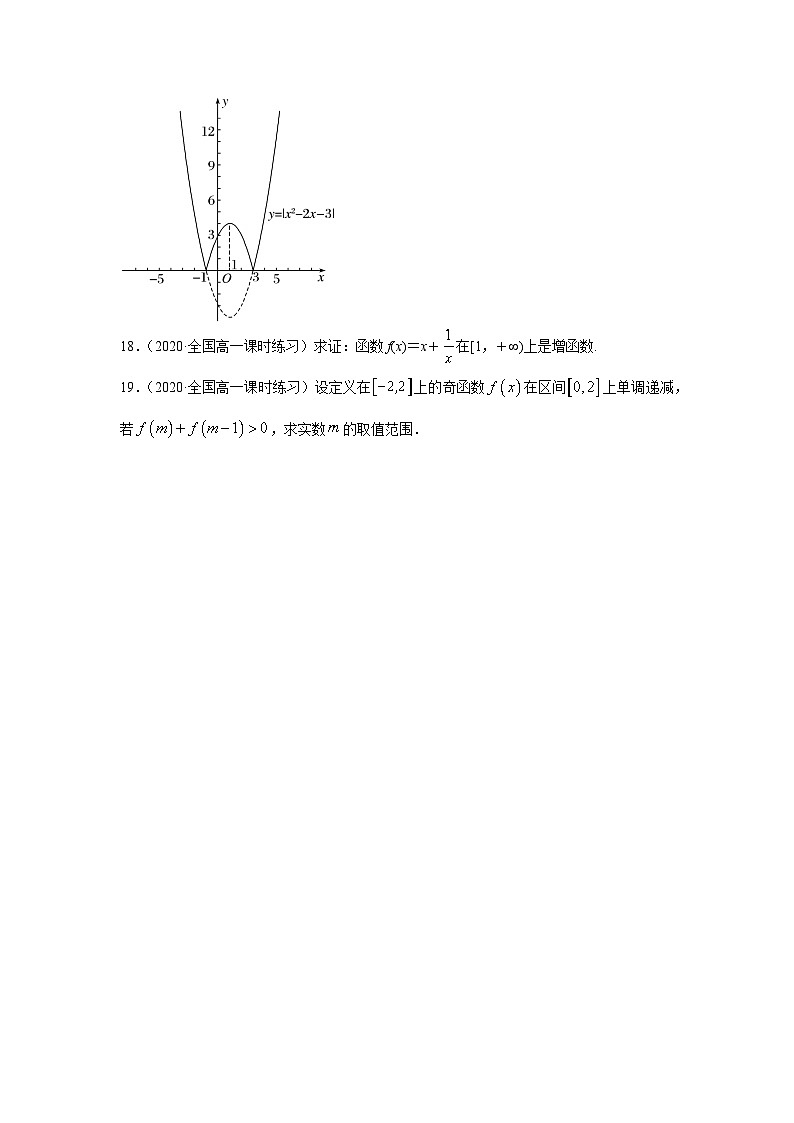
17．（2020·全国高一课时练习）函数y＝|x2－2x－3|的图象如图所示，试写出它的单调区间，并指出单调性.
18．（2020·全国高一课时练习）求证：函数f(x)＝x＋在[1，＋∞)上是增函数.
19．（2020·全国高一课时练习）设定义在上的奇函数在区间上单调递减，若，求实数的取值范围．
宁远县明德湘南高级中学2024年高一期中考试数学试卷
答案
一、
1.【答案】C
2.【答案】C
【详解】因为，所以，解得，所以.
故选：C.
3.【答案】B
【详解】根据题意得，，则中有6个元素，
∴的真子集个数为26﹣1＝63个．
故选：B．
4.【答案】D
5.【答案】B
【分析】本题主要是根据条件判断充分必要性，由所给条件很容易得到答案
【详解】当时，，充分条件成立.
解方程，得或，必要条件不成立.
“”是“”成立的充分不必要条件.
故选：B.
6.【答案】B
7.【答案】C
8.【答案】C
【详解】对子集A分类讨论：
当A是二元集{3，4}时，此时B可以为{1，2，3，4}，{1，3，4}，{2，3，4}，{3，4}，共4结果；
当A是三元集{1，3，4}时，此时B可以为{2，3，4}，{3，4}，共2种结果；
当A是三元集{2，3，4}时，此时B可以为{1，3，4}，{3，4}，共2种结果；
当A是四元集{1，2，3，4}时，此时B取{3，4}，有1种结果，
根据计数原理知共有4+2+2+1＝9种结果．
故选：C．
二、
9.【答案】BD
10.【答案】ABC
11.【答案】ABD
【解析】
由得，A正确；
当时，，则时，，，最大值为1，B正确；
若在上为增函数，则在上为增函数，C错；
若时，，则时，，，D正确．
故选：ABD．
三、
12.
13.【答案】 6 9 8
【详解】，由，解得.
由，解得，故．
所以方程有两个相等的根为3，
所以，且，解得，.
综上知，.，
故答案为：6，9，8
14.【答案】4
【解析】，，
因为，，所以，，
由得，即，解得或，
当时，解得，此时，不满足题意；
当时，解得，满足题意.
所以.故答案为：4
三、
15.【答案】(1)；(2)﹒
【详解】(1)，；
(2)∵，∴．
∵，
∴或，故m的取值范围为：﹒
16.【答案】(1)；(2)当时集合，当时集合；(3)
【详解】(1) 是空集，
且，
，解得，
的取值范围为：；
(2)①当时，集合，
②当时，，
，解得，此时集合，
综上所求，当时集合，当时集合；
(3)中至少有一个元素，则当中只有一个元素时，或；
当中有2个元素时，则且，即，解得且；
综上可得时中至少有一个元素，即
17.【答案】单调增区间为：，；单调减区间为：，
【解析】
由图可知：该函数在区间单调递减，
在区间单调递增，在区间单调递减，
在区间单调递增.
故该函数的单调增区间为：，；
该函数的单调减区间为：，.
18.【答案】证明见详解.
【解析】
证明：在区间上任取，
则
因为，故可得；
又因为，故可得.
故，即.
故在区间上单调递增.
19.【答案】
【解析】
由是奇函数，且，得．
因为在上单调递减，且在上为奇函数，
所以在上单调递减，
则，解得，所以，故实数的取值范围为．
点睛：根据函数增减性和奇偶性求解不等式，可简记为去“”法，当奇函数在对应区间单调递增时，若，则；当奇函数在对应区间单调递减时，若，则