浙教版2024-2025学年九年级数学上册第三次月考训练卷（原卷版）-A4

这是一份浙教版2024-2025学年九年级数学上册第三次月考训练卷（原卷版）-A4，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本题共10题，每题3分，共30分．每小题只有一个选项符合题目要求．
1. 已知，则下列各式正确是（ ）
A. B. C. D.
2. 将抛物线：向左平移3个单位，再向下平移2个单位得到抛物线，则抛物线的函数表达式为（ ）
A. B.
C D.
3. 在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同，小明通过多次试验发现，摸出红球的频率稳定在0.6左右，则袋子中红球的个数最有可能是（ ）
A. 5B. 8C. 12D. 15
4. 已知一个扇形的圆心角为，半径是6，则这个扇形的面积是（ ）
A. B. C. D.
5. 港珠澳大桥是世界上最长的跨海大桥，被誉为“现代世界七大奇迹”的超级工程，它是我国从桥梁大国走向桥梁强国的里程碑之作．港珠澳大桥主桥为三座大跨度钢结构斜拉桥，其中九洲航道桥主塔造型取自“风帆”，寓意“扬帆起航”．某校九年学生为了测量该主塔的高度，站在B处看塔顶A，仰角为，然后向后走160米（米），到达C处，此时看塔顶A，仰角为，则该主塔的高度是（ ）

A. 80米B. 米C. 160米D. 米
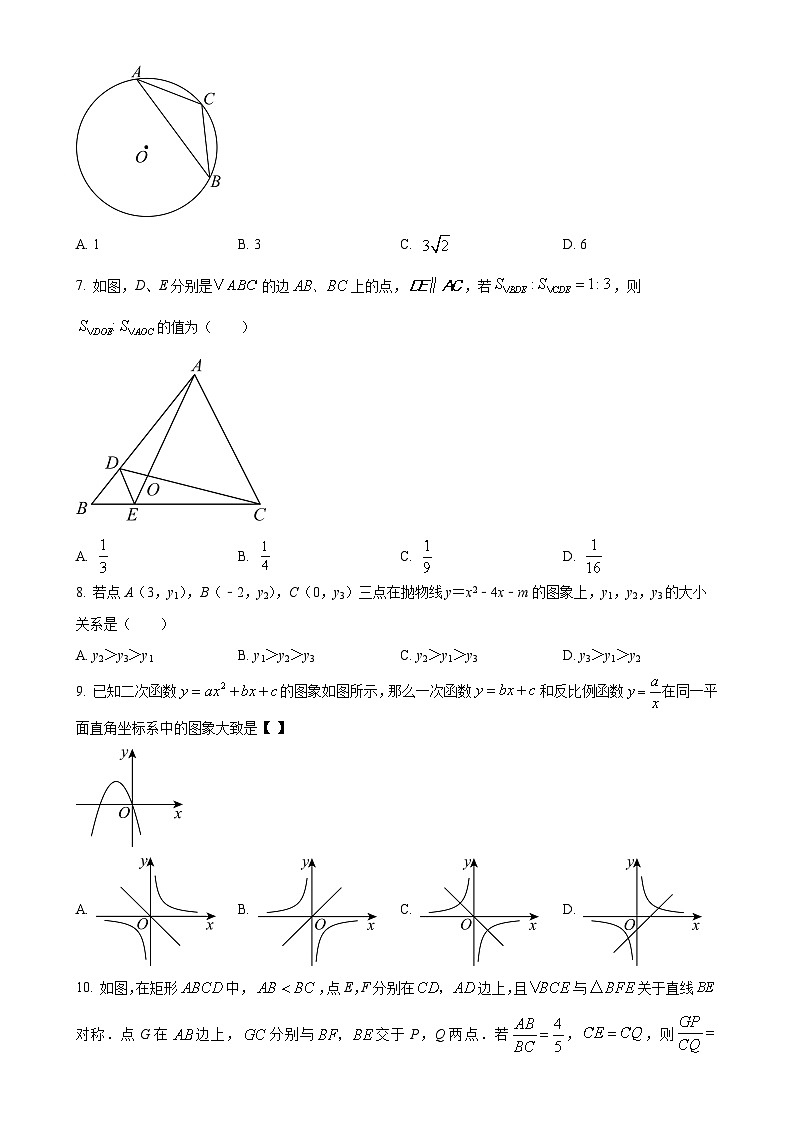
6. 如图，是内接三角形，已知，，则的半径为（ ）
A. 1B. 3C. D. 6
7. 如图，D、E分别是的边上的点，，若，则的值为（ ）

A. B. C. D.
8. 若点A（3，y1），B（﹣2，y2），C（0，y3）三点在抛物线y＝x2﹣4x﹣m的图象上，y1，y2，y3的大小关系是（ ）
A. y2＞y3＞y1B. y1＞y2＞y3C. y2＞y1＞y3D. y3＞y1＞y2
9. 已知二次函数的图象如图所示，那么一次函数和反比例函数在同一平面直角坐标系中的图象大致是【 】
A. B. C. D.
10. 如图，在矩形中，，点E，F分别在边上，且与关于直线对称．点G在边上，分别与交于P，Q两点．若，，则（ ）
A B. C. D.
二、填空题：（本大题共6个小题．每小题4分，共24分．把答案填在题中横线上．）
11. 现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片，卡片除正面图案不同外，其余均相同，将三张卡片正面向下洗匀，从中随机抽取一张卡片，则抽出的卡片图案是琮琮的概率是___________．

12. 如图是某商场自动扶梯的示意图，自动扶梯AB的倾斜角为30°，在自动扶梯下方地面C处测得扶梯顶端B的仰角为60°，A、C之间的距离为6m，则自动扶梯的垂直高度BD=_________m．（结果保留根号）．
13. 五水共治办公室在一次巡查时测量一排水管的排水情况，如图，水平放置的圆柱形排水管的截面为，半径是，有水部分弓形的高为，则______．
14. 如图，某同学利用镜面反射的原理巧妙地测出了树的高度，已知人的站位点，镜子，树底三点在同一水平线上，眼睛与地面的高度为米，米，米，则树高为______米．

15. 如图，一张扇形纸片的圆心角为，半径为6．将这张扇形纸片折叠，使点与点恰好重合，折痕为，则阴影部分的面积为______________．
16. 在平面直角坐标系中，一次函数和，无论取何值，始终有，则的取值为______．
三、解答题：（本大题共8个小题，共66分，解答应写出文字说明、证明过程或演算步骤）
17. 为了解学生艺术特长发展情况，某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其他活动项目中，你最喜欢哪一项活动（每人只限一项）”的问题，在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制成如下两幅不完整的统计图．
请你根据统计图解答下列问题：
（1）在这次调查中一共抽查了__________名学生，其中，喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为__________，喜欢“戏曲”活动项目的人数是__________人；
（2）若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组，请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率．
18. 如图1是一台手机支架，图2是其侧面示意图，，可分别绕点A，B转动，测量知，．当，转动到，时，求点C到的距离（参考数据：）

19. 如图，为的直径，弦于点E，连接，．
（1）求证：；
（2）若，，求的长．
20. 如图，在平行四边形中，过点A作，垂足为E，连接，F为线段上一点，且．
（1）求证：；
（2）若，求的长．
21. 如图，有长为的篱笆，一面利用墙（墙的最大可用长度为）围成中间隔有一道篱笆的长方形养鸡场，设养鸡场的宽为，长为，面积为．
（1）求y与x的函数关系，并写出x的取值范围；
（2）当长方形的长、宽各为多少时，养鸡场的面积最大，最大面积是多少？
22. （1）如图1，和均为等边三角形，直线和直线交于点F．填空：
①线段，之间的数量关系为________；②的度数为______．
（2）如图2所示，和均为等腰直角三角形，，直线和直线交于点F，请判断的度数及线段，之间的数量关系，并说明理由．
（3）如图3所示，和均为直角三角形，，，当点B在线段的延长线上时，求线段和的长度．
23. 如图，在平面直角坐标系中，已知抛物线与直线AB相交于A，B两点，其中A(-3,-4)，B(0,-1)．
(1)求该抛物线的函数表达式．
(2)点P为直线AB下方抛物线上的任意一点，连接PA，PB，求△PAB面积的最大值．
(3)在二次函数的对称轴上找一点C，使得△ABC是等腰三角形，求满足条件的点C的坐标．
24. 锐角内接于，若上有一点D，连接，交于点F，且．
（1）如图1，回答下列问题：
①求证：．
②若点M在线段上（不与点A，点F重合），点N在线段上（不与点M，点F重合），，求证．
（2）如图2，若，求．