2024-2025学年辽宁省沈阳126中教育集团九年级（上）期中数学试卷（含解析）

这是一份2024-2025学年辽宁省沈阳126中教育集团九年级（上）期中数学试卷（含解析），共36页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
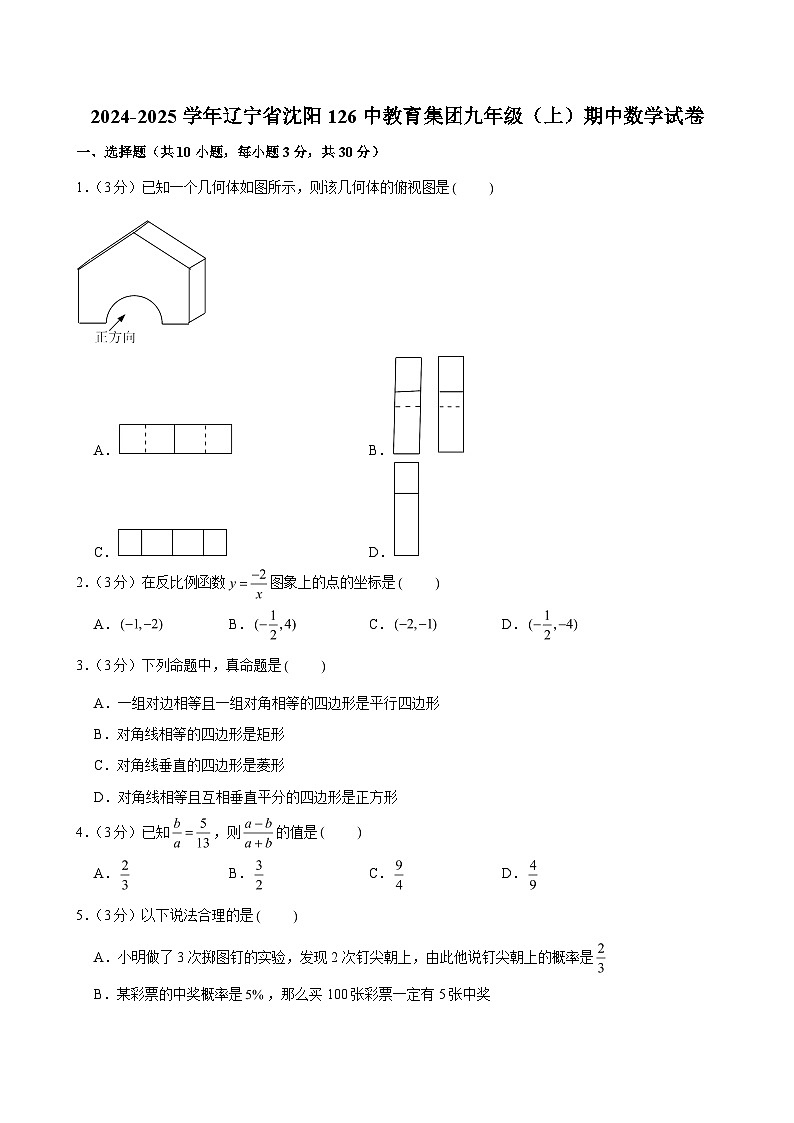
1．（3分）已知一个几何体如图所示，则该几何体的俯视图是
A．B．
C．D．
2．（3分）在反比例函数图象上的点的坐标是
A．B．C．D．
3．（3分）下列命题中，真命题是
A．一组对边相等且一组对角相等的四边形是平行四边形
B．对角线相等的四边形是矩形
C．对角线垂直的四边形是菱形
D．对角线相等且互相垂直平分的四边形是正方形
4．（3分）已知，则的值是
A．B．C．D．
5．（3分）以下说法合理的是
A．小明做了3次掷图钉的实验，发现2次钉尖朝上，由此他说钉尖朝上的概率是
B．某彩票的中奖概率是，那么买100张彩票一定有5张中奖
C．某射击运动员射击一次只有两种可能的结果：中靶与不中靶，所以他击中靶的概率是
D．小明做了3次掷均匀硬币的实验，其中有一次正面朝上，2次正面朝下，他认为再掷一次，正面朝上的概率还是
6．（3分）用配方法解一元二次方程，此方程可变形为
A．B．C．D．
7．（3分）有两根电线杆在地面上形成了各自的影子，若以电线杆与其影子分别作为三角形的两边，可以得到两全等三角形，则这种投影现象为
A．平行投影
B．中心投影
C．既不是平行投影也不是中心投影
D．可能是平行投影也可能是中心投影
8．（3分）如图，，，其中，的长为
A．B．C．D．6
9．（3分）如图，矩形为一个正在倒水的水杯的截面图，，杯中水面与的交点为，当水杯底面与水平面的夹角为时，杯中水的最大深度为
A．9B．15C．D．
10．（3分）如图，四边形和都是平行四边形，点在边上，且，连接分别交，于点，，设△与△面积的比为，则的值为
A．B．C．D．
二、填空题（本题共5小题，每小题3分，共15分）
11．（3分）在一个不透明的袋子里有红球、黄球共15个，这些球除颜色外都相同，小明通过多次实验发现，摸到红球的频率稳定在0.4左右，则袋子中黄球的个数可能是 个．
12．（3分）若为锐角，且，则的值为 ．
13．（3分）三个顶点的坐标分别为，，，以原点为位似中心，相似比为，将缩小，则点的对应点的坐标是 ．
14．（3分）如图，点在反比例函数的图象上，点在轴正半轴上，直线交轴于点，若，△的面积为3，则的值为 ．
15．（3分）如图，，，，，，，，求 ．
三、解答题（本题共8道小题，共75分）
16．（10分）（1）计算：．
（2）解方程：．
17．（8分）某校一年级开设人数相同的四个班级，分别是1班，2班，3班，4班，甲、乙两位学生是该校一年级新生，开学初学校对所有一年级新生进行电脑随机分班．
（1）“学生甲分到1班”的概率是 ；
（2）请用画树状图法或列表法，求甲、乙两名新生分到相邻两个班级的概率．
18．（7分）如图，中，点是的中点，连结并延长交的延长线于点．
（1）求证：；
（2）点是线段上一点，满足，交于点，若，，求的长．
19．（10分）如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于、两点．
（1）求一次函数和反比例函数的解析式；
（2）观察图象，直接写出不等式的解集 ；
（3）若是轴上一点，且满足△是直角三角形，直接写出点的坐标 ．
20．（9分）如图，在中，，，，动点从点出发沿边向点以的速度移动，同时动点从点出发沿边向点以的速度移动，当运动到点时、两点同时停止运动，设运动时间为．
（1） ； ；（用的代数式表示）
（2）是的中点，连接、，为何值时的面积为？
21．（9分）大连市中山公园原址为一个叫做刘家屯的小山头，1898年沙俄强占旅大期间，将这里改为绿地．日占时期改为圣德公园，圣德公园多次作为我地下党的接头地点，传递了许多抗日情报．大连解放后的1945年11月，大连市政府为纪念孙中山先生，改名中山公园，并历经多年修建了5个小亭，其中敬闲亭位于山头最高处．
“勿忘国耻，怀念先烈，吾辈自强”．某中学超越小组的同学们，带着测量工具来到中山公园，为测量敬闲亭设计了如下方案，请你根据以下材料，完成项目任务．
22．（13分）【初识图形】
（1）如图1，、分别为正方形边和边上的点，连接、，且．则 ．
（2）如图2，矩形中，点、分别在边、上，连接、，且，，，求的值．
【类比探究】
（3）如图3，△中，、分别为、边上的点，，，为中点，连接，作交于点，交于．直接写出的长为 ．
【拓展迁移】
（4）在矩形中，，，点、分别为线段和线段边上的一点，以为折痕，将四边形翻折，得到四边形，直线和直线分别交直线于点和点，且，．
①请直接写出线段的长 ．
②若点、分别为线段和线段边上的动点，满足．且直线始终经过一个定点，求的最大值 ．
23．（9分）定义：在平面直角坐标系中，点是某函数图象上的一点，作该函数图象中自变量大于的部分关于直线的轴对称图形，与原函数图象中自变量大于或等于的部分共同构成一个新函数的图象，则这个新函数叫做原函数关于点的“友好函数”．
例如：图①是函数的图象，则它关于点的“友好函数”的图象如图②所示，且它的“友好函数”的解析式为．
（1）直接写出函数关于点的“友好函数”的解析式．
（2）如图③，点是函数的图象上的一点，设点的横坐标为，是函数关于点的“友好函数”．
①当时，若函数的函数值取值范围是，直接写出自变量的取值范围 ；
②如图④，当以点、、、为顶点的矩形与函数的图象只有1个公共点时，直接写出的取值范围 ．
（3）①当（2）②中的函数的图象与矩形有且仅有一个公共点时，在函数上是存在一点，使△是以为直角边的直角三角形，请直接写出所有符合条件的点的坐标 ；
②当（2）中“主题干”中的函数的对称轴左侧图象与（2）②中矩形的边所围成的三角形图形中，其面积为时，直接写出点的坐标 ．
参考答案
一、选择题（本题共10小题，每小题3分，共30分）
1．（3分）已知一个几何体如图所示，则该几何体的俯视图是
A．B．
C．D．
解：从上面可看，是一个矩形，矩形的中间有一条纵向的实线，实线的两侧分别有一条纵向的虚线．
故选：．
2．（3分）在反比例函数图象上的点的坐标是
A．B．C．D．
解：对于选项，当时，，
点不是反比例函数数图象上的点；
对于选项，当时，，
点 是反比例函数图象上的点；
对于选项，当时，，
点不是反比例函数图象上的点；
对于选项，当时，，
点 不是反比例函数图象上的点．
故选：．
3．（3分）下列命题中，真命题是
A．一组对边相等且一组对角相等的四边形是平行四边形
B．对角线相等的四边形是矩形
C．对角线垂直的四边形是菱形
D．对角线相等且互相垂直平分的四边形是正方形
解：、一组对边相等且一组对角相等的四边形是平行四边形；假命题；
、对角线相等的四边形是矩形；假命题；
、对角线垂直的四边形是菱形；假命题；
、对角线相等且互相垂直平分的四边形是正方形；真命题；
故选：．
4．（3分）已知，则的值是
A．B．C．D．
解：设，
则，，
；
故选：．
5．（3分）以下说法合理的是
A．小明做了3次掷图钉的实验，发现2次钉尖朝上，由此他说钉尖朝上的概率是
B．某彩票的中奖概率是，那么买100张彩票一定有5张中奖
C．某射击运动员射击一次只有两种可能的结果：中靶与不中靶，所以他击中靶的概率是
D．小明做了3次掷均匀硬币的实验，其中有一次正面朝上，2次正面朝下，他认为再掷一次，正面朝上的概率还是
解：小明做了3次掷图钉的实验，发现2次钉尖朝上，由此他说钉尖朝上的概率是是错误的，3次试验不能总结出概率，故选项错误，
某彩票的中奖概率是，那么买100张彩票可能有5张中奖，但不一定有5张中奖，故选项错误，
某射击运动员射击一次只有两种可能的结果：中靶与不中靶，所以他击中靶的概率是不正确，中靶与不中靶不是等可能事件，故选项错误，
小明做了3次掷均匀硬币的实验，其中有一次正面朝上，2次正面朝下，他认为再掷一次，正面朝上的可能性是，故选项正确，
故选：．
6．（3分）用配方法解一元二次方程，此方程可变形为
A．B．C．D．
解：，
，
，
，
故选：．
7．（3分）有两根电线杆在地面上形成了各自的影子，若以电线杆与其影子分别作为三角形的两边，可以得到两全等三角形，则这种投影现象为
A．平行投影
B．中心投影
C．既不是平行投影也不是中心投影
D．可能是平行投影也可能是中心投影
解：根据题意只知道电线杆与其影子分别作为三角形的两边，可以得到两全等三角形，平行投影和中心投影都可能出现这种情况，所以可能是平行投影也可能是中心投影．故选．
8．（3分）如图，，，其中，的长为
A．B．C．D．6
解：，
，
，
，
，
．
故选：．
9．（3分）如图，矩形为一个正在倒水的水杯的截面图，，杯中水面与的交点为，当水杯底面与水平面的夹角为时，杯中水的最大深度为
A．9B．15C．D．
解：过点作，垂足为．如图．
四边形为矩形，
．
，
．
在中，
，
．
故选：．
10．（3分）如图，四边形和都是平行四边形，点在边上，且，连接分别交，于点，，设△与△面积的比为，则的值为
A．B．C．D．
解：四边形是平行四边形，
，且，，
四边形是平行四边形，
，且，
，
，，
是△的中位线，
，，
设，
，
，，，
，
，
△△，
，
，，
，
，
，而△和△同高，
，
．
故选：．
二、填空题（本题共5小题，每小题3分，共15分）
11．（3分）在一个不透明的袋子里有红球、黄球共15个，这些球除颜色外都相同，小明通过多次实验发现，摸到红球的频率稳定在0.4左右，则袋子中黄球的个数可能是 9 个．
解：摸到红球的频率稳定在0.4左右，
袋子中红球的个数可能是（个，
袋子中黄球的个数可能（个，
故答案为：9．
12．（3分）若为锐角，且，则的值为 ．
解：为锐角，，
，
，
．
故答案为：．
13．（3分）三个顶点的坐标分别为，，，以原点为位似中心，相似比为，将缩小，则点的对应点的坐标是 或 ．
解：以原点为位似中心，相似比为，将缩小，，
点的对应点的坐标为，或，，即或，
故答案为：或．
14．（3分）如图，点在反比例函数的图象上，点在轴正半轴上，直线交轴于点，若，△的面积为3，则的值为 ．
解：作轴于，
设点坐标为，则，，
，，
，
，
，
．
故答案为：．
15．（3分）如图，，，，，，，，求 ．
解：过点作于，过点作于，在上取一点，使，如图所示：
，，
，
四边形是矩形，
，，，
，，
，
在△中，由勾股定理得：，
点是的中点，
，
，，
是线段的垂直平分线，，
设，
，
，
，
，
，
，
又，
△△，
，
，
，
，，
，
又，
△△，
，
，
，
，
，
，
解得：．
．
故答案为：．
三、解答题（本题共8道小题，共75分）
16．（10分）（1）计算：．
（2）解方程：．
解：（1）原式
．
（2），
，
，
，
则，
所以．
17．（8分）某校一年级开设人数相同的四个班级，分别是1班，2班，3班，4班，甲、乙两位学生是该校一年级新生，开学初学校对所有一年级新生进行电脑随机分班．
（1）“学生甲分到1班”的概率是 ；
（2）请用画树状图法或列表法，求甲、乙两名新生分到相邻两个班级的概率．
解：（1）由题意知，共有4种等可能的结果，其中“学生甲分到1班”的结果有1种，
“学生甲分到1班”的概率为，
故答案为：；
（2）画树状图如下：
共有16种等可能的结果，其中甲、乙两名新生分到相邻两个班级的结果有6种，
甲、乙两名新生分到相邻两个班级的概率．
18．（7分）如图，中，点是的中点，连结并延长交的延长线于点．
（1）求证：；
（2）点是线段上一点，满足，交于点，若，，求的长．
【解答】（1）证明：四边形是平行四边形，
，，
，，
是的中点，
，
，
，
，
，
；
（2）解：，，
，
，
四边形是平行四边形，
，
，，
，
，
，
，
，即，
，
．
19．（10分）如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于、两点．
（1）求一次函数和反比例函数的解析式；
（2）观察图象，直接写出不等式的解集 或 ；
（3）若是轴上一点，且满足△是直角三角形，直接写出点的坐标 ．
解：（1）将点、的坐标代入反比例函数表达式得：，
则，，
即点，反比例函数表达式为：，
由题意得：，解得：，
则一次函数的表达式为：；
（2）观察图象知，直接写出不等式的解集为：或，
故答案为：或；
（3）设点，
由、、的坐标得，，，，
当为斜边时，
则，则，
即点；
当或为斜边时，
同理可得：或，
解得：或3或，
即点或或，
综上，或或或，
故答案为：或或或．
20．（9分）如图，在中，，，，动点从点出发沿边向点以的速度移动，同时动点从点出发沿边向点以的速度移动，当运动到点时、两点同时停止运动，设运动时间为．
（1） ； ；（用的代数式表示）
（2）是的中点，连接、，为何值时的面积为？
解：（1）根据题意得：，，
所以，
故答案为：；；
（2）如图，过点作于，
，即．
．
又是的中点，
，是的中位线．
．
根据题意，得，
整理，得．
解得：，，
即当或4时，的面积是．
21．（9分）大连市中山公园原址为一个叫做刘家屯的小山头，1898年沙俄强占旅大期间，将这里改为绿地．日占时期改为圣德公园，圣德公园多次作为我地下党的接头地点，传递了许多抗日情报．大连解放后的1945年11月，大连市政府为纪念孙中山先生，改名中山公园，并历经多年修建了5个小亭，其中敬闲亭位于山头最高处．
“勿忘国耻，怀念先烈，吾辈自强”．某中学超越小组的同学们，带着测量工具来到中山公园，为测量敬闲亭设计了如下方案，请你根据以下材料，完成项目任务．
解：（1）延长交于点，
由题意得：，，，
设 ，
，
，，
在△中，，
，
在△中，，
，
，
解得：，
，
，
敬闲亭的高度的长约为；
（2）由（1）可得：，
敬闲亭底面圆的半径的长，约，
故答案为：4；
（3）由题意得：，
，，
，
的距离，约，
故答案为：22．
22．（13分）【初识图形】
（1）如图1，、分别为正方形边和边上的点，连接、，且．则 1 ．
（2）如图2，矩形中，点、分别在边、上，连接、，且，，，求的值．
【类比探究】
（3）如图3，△中，、分别为、边上的点，，，为中点，连接，作交于点，交于．直接写出的长为 ．
【拓展迁移】
（4）在矩形中，，，点、分别为线段和线段边上的一点，以为折痕，将四边形翻折，得到四边形，直线和直线分别交直线于点和点，且，．
①请直接写出线段的长 ．
②若点、分别为线段和线段边上的动点，满足．且直线始终经过一个定点，求的最大值 ．
解：（1）四边形是正方形，
，，
，
，，
，
在△和△中，
，
△△，
，
，
故答案为：1；
（2）如图，过点作于点，
四边形是矩形，，，
，，，
四边形是矩形，，
，
于点，
，
，
，
，
即，
，
；
（3）如图所示，过点作于点，
△是直角三角形，，，，
，
点是的中点，
，
在△中，，，
，
设，
，，
△△，
，
即，
，，
，
，
，
，
又 ，
△△，
，
即，
解得，
，
故答案为：；
（4）①四边形是矩形，
，，
四边形翻折，得到四边形，
，，，，
第一种情况，如图，过点作于点，
，，，
，
，，
，
四边形是矩形，
，
，
，且，
△△，
，
即，
，
，，
；
第二种情况，如图，设与交于点，
同理，，，，
，
，，
△△，
，
即 ，
，，
，，
，，
△△，
，
即 ，
，
，
；
综上所述，的长为或；
故答案为：或；
②如图，
四边形是矩形，
，
，直线始终经过一个定点，
延长，交于点，
△△，
，且，
，
解得，
如图，以点坐标原点，为正方向作横轴，方向为纵轴作平面直角坐标系，
，
设，则，
，，即，
，
令，
，
函数图象开口向上，随的增大而增大，
当时，有最大值，且最大值为，
的最大值为，
故答案为：．
23．（9分）定义：在平面直角坐标系中，点是某函数图象上的一点，作该函数图象中自变量大于的部分关于直线的轴对称图形，与原函数图象中自变量大于或等于的部分共同构成一个新函数的图象，则这个新函数叫做原函数关于点的“友好函数”．
例如：图①是函数的图象，则它关于点的“友好函数”的图象如图②所示，且它的“友好函数”的解析式为．
（1）直接写出函数关于点的“友好函数”的解析式．
（2）如图③，点是函数的图象上的一点，设点的横坐标为，是函数关于点的“友好函数”．
①当时，若函数的函数值取值范围是，直接写出自变量的取值范围 ；
②如图④，当以点、、、为顶点的矩形与函数的图象只有1个公共点时，直接写出的取值范围 ．
（3）①当（2）②中的函数的图象与矩形有且仅有一个公共点时，在函数上是存在一点，使△是以为直角边的直角三角形，请直接写出所有符合条件的点的坐标 ；
②当（2）中“主题干”中的函数的对称轴左侧图象与（2）②中矩形的边所围成的三角形图形中，其面积为时，直接写出点的坐标 ．
【解答】（1）解：如下图所示，
函数关于点的“友好函数”的解析式为；
（2）①解：如下图所示，
当时，函数关于点的“友好函数”是，
当时，可得，
解得：，
当时，可得，
解得：，
综上所述，当时，的取值范围是；
故答案为：；
②矩形与函数的图象只有一个公共点是，则“友好函数”只能经过点，
设左侧的函数解析式为，
把点的坐标代入可得：，
解得：，
此时在点左侧的函数解析式为，
点也在函数上，
，
解得：；
故答案为：；
（3）解：①如下图所示，
由（2）可知，
设点的坐标为，
点、，
，
，
，
当为斜边时，，
，
解得，
此时，
点坐标为；
当为斜边时，，
，
解得，
此时，
点坐标为，；
综上，点的坐标为或，；
故答案为：或，；
②如下图所示，
当△的面积为时，设点的坐标为，则，
设函数左侧的函数解析式为，
则有，
解得：，
函数左侧的函数解析式为，
点的横坐标为3，
点的纵坐标为，
，
，
，
解得：或（舍，
当时，点的坐标为，
把点的坐标代入，可得：，
解得：，
函数左侧的函数解析式为，
联立方程组，
解得，
点的坐标为；
当△的面积为时，设点的坐标为，则，
设函数左侧的函数解析式为，
则有，
解得：，
函数左侧的函数解析式为，
点的横坐标为，
点的纵坐标为，
，
，
解得：或（舍，
当时，点的坐标为，
把点的坐标代入可得：，
解得：，
函数左侧的函数解析式为，
联立方程组，
解得，
点的坐标为，
综上所述点的坐标为或，
故答案为：或．
项目
测量敬闲亭的高度及底面圆的半径
测量工具
测角仪、皮尺等
测量

说明：点为亭底面圆圆心，在、处分别测得亭顶端的仰角为、，、测角仪高度，测角仪所在位置与亭底部边缘距离，点、、、在同一条直线上．
参考数据
，，，，，最后结果保留．
项目任务
（1）
求敬闲亭的高度的长．
（2）
直接写出敬闲亭底面圆的半径的长，约 米．
（3）
直接写出的距离，约 米．
项目
测量敬闲亭的高度及底面圆的半径
测量工具
测角仪、皮尺等
测量

说明：点为亭底面圆圆心，在、处分别测得亭顶端的仰角为、，、测角仪高度，测角仪所在位置与亭底部边缘距离，点、、、在同一条直线上．
参考数据
，，，，，最后结果保留．
项目任务
（1）
求敬闲亭的高度的长．
（2）
直接写出敬闲亭底面圆的半径的长，约 4 米．
（3）
直接写出的距离，约 米．