北师大版数学七上期末考点提升练习专题32 数据的收集与整理（2份，原卷版+解析版）

这是一份北师大版数学七上期末考点提升练习专题32 数据的收集与整理（2份，原卷版+解析版），文件包含北师大版数学七上期末考点提升练习专题32数据的收集与整理原卷版doc、北师大版数学七上期末考点提升练习专题32数据的收集与整理解析版doc等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。
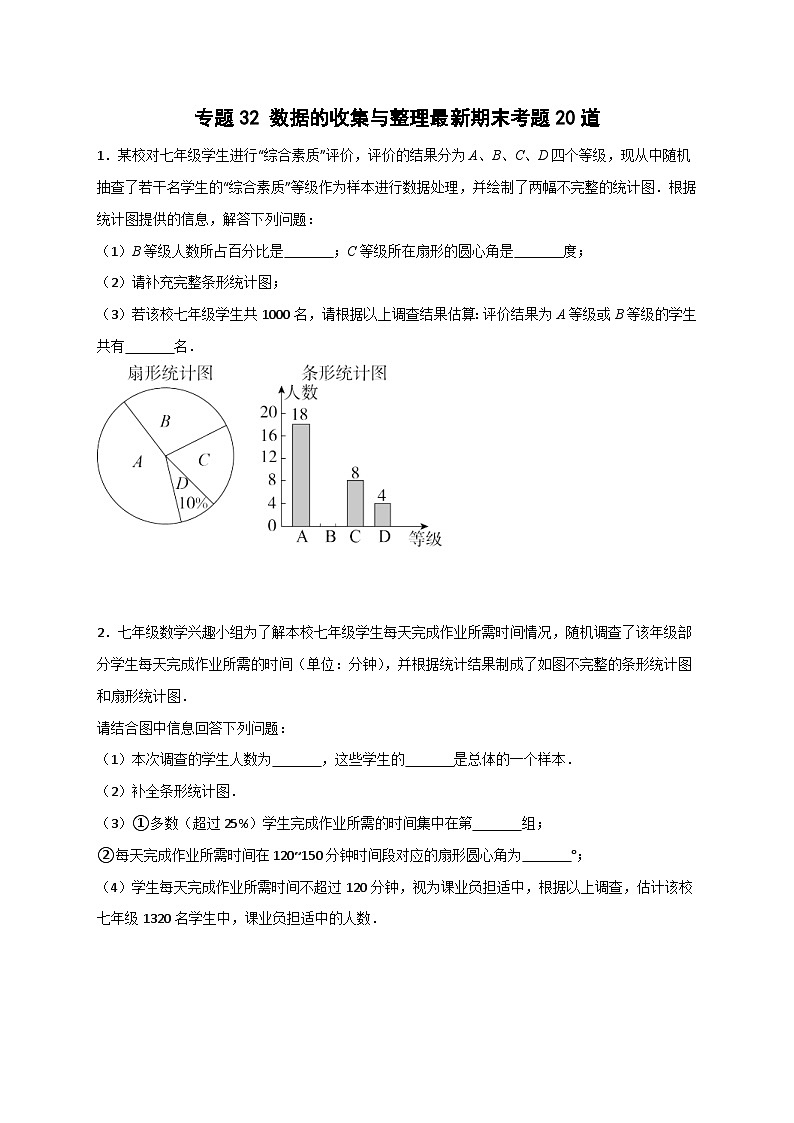
（1）B等级人数所占百分比是 ；C等级所在扇形的圆心角是 度；
（2）请补充完整条形统计图；
（3）若该校七年级学生共1000名，请根据以上调查结果估算：评价结果为A等级或B等级的学生共有 名．
【答案】（1）25%；72；（2）见解析；（3）700．
【分析】（1）先根据D等级人数及其所占百分比求出被调查的总人数，再由四个等级人数之和等于总人数求出B等级人数，最后用B等级人数除以总人数可得答案，再用360°乘以C等级人数所占比例可得答案；
（2）根据（1）中计算结果可补全条形图；
（3）用总人数乘以样本中A、B等级人数和所占比例即可．
【详解】解：（1）∵被调查的人数为4÷10%＝40（人），
∴B等级人数为40﹣（18+8+4）＝10（人），
则B（良好）等级人数所占百分比是 SKIPIF 1 < 0 ×100%＝25%，
在扇形统计图中，C（合格）等级所在扇形的圆心角度数是360°× SKIPIF 1 < 0 ＝72°，
故答案为：25%；72；
（2）补全条形统计图如下：
；
（3）估计评价结果为A（优秀）等级或B（良好）等级的学生共有1000× SKIPIF 1 < 0 ＝700（人）．
故答案为：700．
【点睛】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据，扇形统计图直接反映部分占总体的百分比大小．
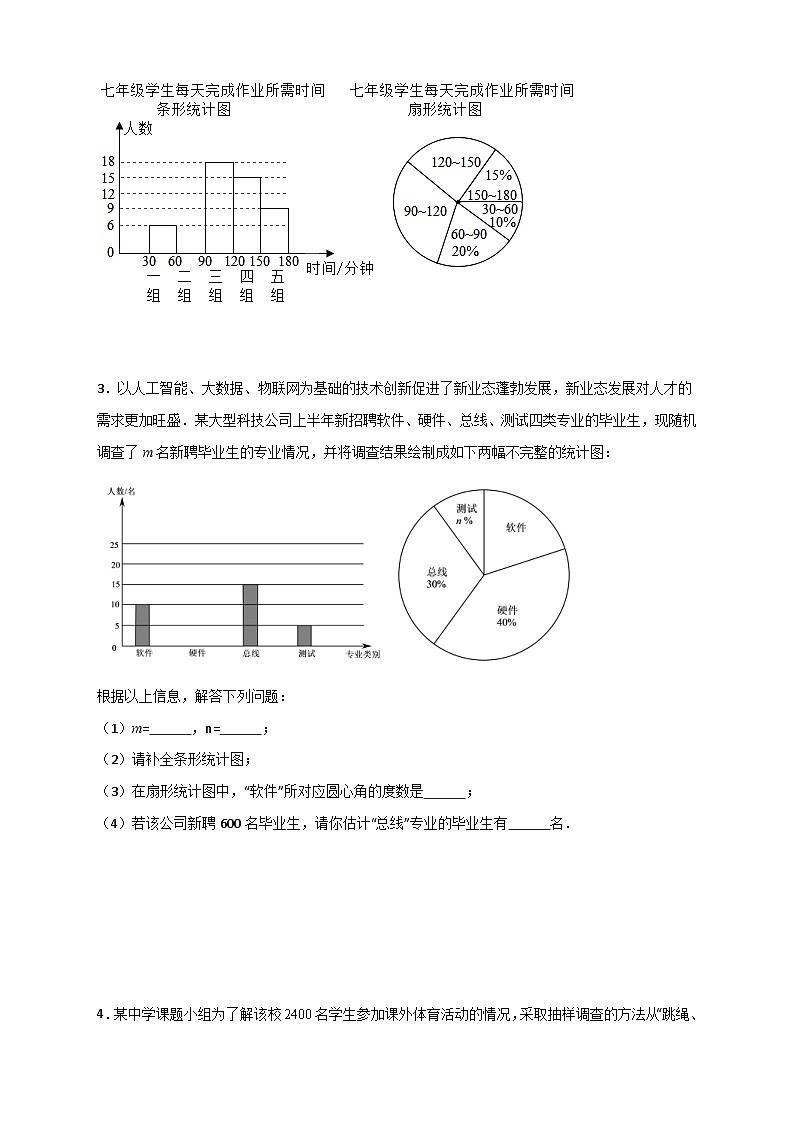
2．七年级数学兴趣小组为了解本校七年级学生每天完成作业所需时间情况，随机调查了该年级部分学生每天完成作业所需的时间（单位：分钟），并根据统计结果制成了如图不完整的条形统计图和扇形统计图．
请结合图中信息回答下列问题：
（1）本次调查的学生人数为 ，这些学生的 是总体的一个样本．
（2）补全条形统计图．
（3）①多数（超过25%）学生完成作业所需的时间集中在第 组；
②每天完成作业所需时间在120~150分钟时间段对应的扇形圆心角为 °；
（4）学生每天完成作业所需时间不超过120分钟，视为课业负担适中，根据以上调查，估计该校七年级1320名学生中，课业负担适中的人数．
【答案】（1）60，每天完成作业所需的时间；（2）见解析；（3）①三；②90；（4）792人
【分析】（1）由作业完成时间在30~60的人数及其所占百分比可得总人数，根据样本的概念可得答案；
（2）总人数乘以60~90时间段的人数所占百分比即可；
（3）①求出第三组人数所占百分比即可得出答案；②用360°乘以完成作业所需时间在120~150分钟时间段人数所占比例；
（4）用总人数乘以样本中第一、二、三组人数和所占比例即可．
【详解】解：（1）本次调查的学生人数为：6÷10%=60（人），
这些学生的每天完成作业所需的时间是总体的一个样本，
故答案为：60，每天完成作业所需的时间；
（2）60~90时间段的人数有：60×20%=12（人），补全统计图如下：
（3）①∵第三组人数所占百分比为 SKIPIF 1 < 0 ×100%=30%，
∴多数（超过25%）学生完成作业所需的时间集中在第三组；
②每天完成作业所需时间在120~150分钟时间段对应的扇形圆心角为360°× SKIPIF 1 < 0 =90°；
故答案为：三、90；
（4）估计该校七年级1320名学生中，课业负担适中的人数为1320× SKIPIF 1 < 0 =792（人）．
【点睛】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
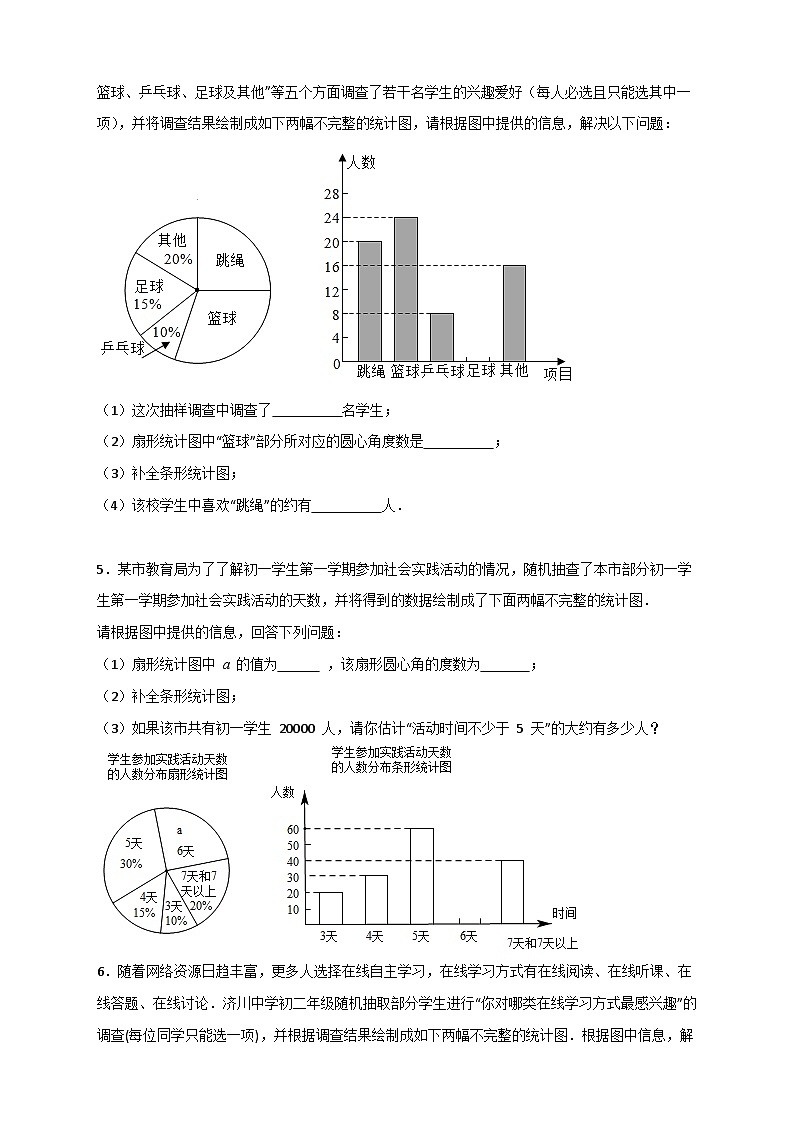
3．以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展，新业态发展对人才的需求更加旺盛．某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生，现随机调查了m名新聘毕业生的专业情况，并将调查结果绘制成如下两幅不完整的统计图：
根据以上信息，解答下列问题：
（1）m= ，n= ；
（2）请补全条形统计图；
（3）在扇形统计图中，“软件”所对应圆心角的度数是 ；
（4）若该公司新聘600名毕业生，请你估计“总线”专业的毕业生有 名．
【答案】（1）50，10；（2）补全条形统计图见解析；（3）70°；（4）估计“总线”专业的毕业生有180名．
【分析】(1)根据条形统计图和扇形统计图的数据计算即可．
(2)先算出硬件专业的毕业生人数,再补充统计图即可．
(3)先算出软件专业的占比,再利用周角相乘即可算出圆心角．
(4)用600与总线所占比相乘即可求出．
【详解】（1）由统计图可知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，n=10．
（2）硬件专业的毕业生为 SKIPIF 1 < 0 人，则统计图为
（3）软件专业的毕业生对应的占比为 SKIPIF 1 < 0 ，所对的圆心角的度数为 SKIPIF 1 < 0 ．
（4）该公司新聘600名毕业生，“总线”专业的毕业生为 SKIPIF 1 < 0 名．
【点睛】本题考查条形统计图和扇形统计图的画图和信息获取,关键在于通过图象获取有用信息．
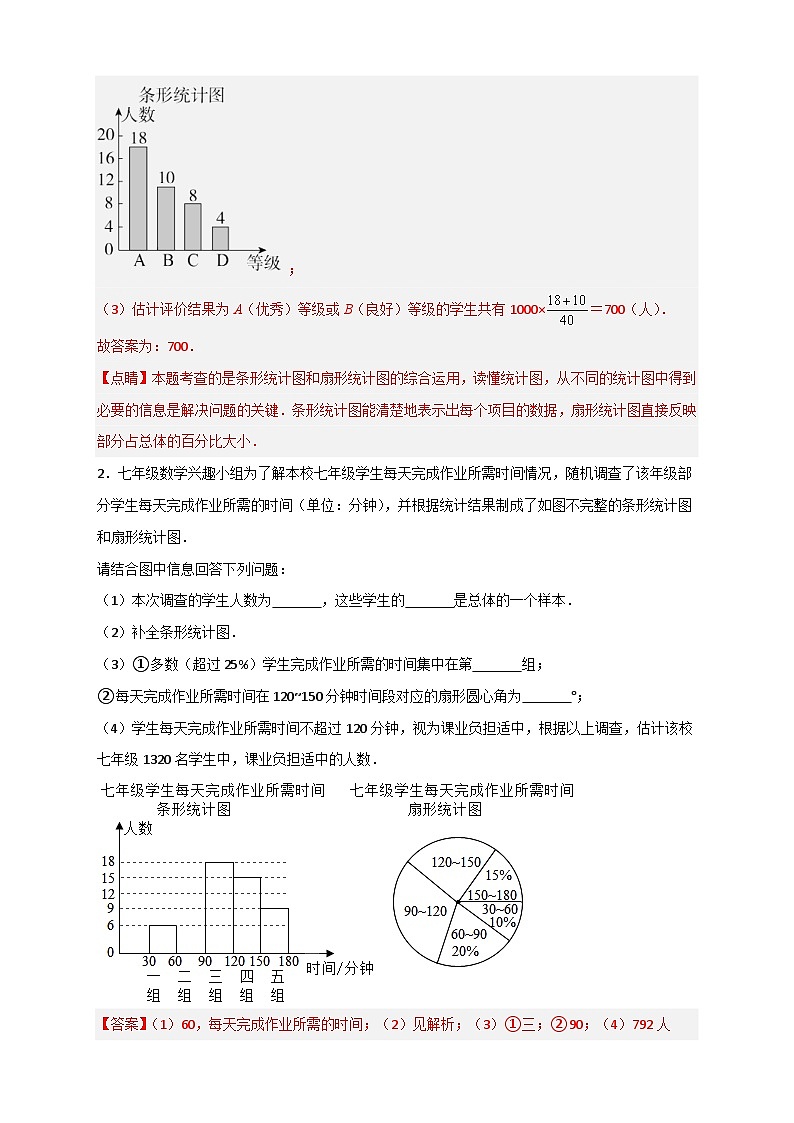
4．某中学课题小组为了解该校 SKIPIF 1 < 0 名学生参加课外体育活动的情况，采取抽样调查的方法从“跳绳、篮球、乒乓球、足球及其他”等五个方面调查了若干名学生的兴趣爱好（每人必选且只能选其中一项），并将调查结果绘制成如下两幅不完整的统计图，请根据图中提供的信息，解决以下问题：
（1）这次抽样调查中调查了 名学生；
（2）扇形统计图中“篮球”部分所对应的圆心角度数是 ；
（3）补全条形统计图；
（4）该校学生中喜欢“跳绳”的约有 人．
【答案】（1）80；（2）108°；（3）见解析；（4）600
【分析】（1）根据选择乒乓球的人数和所占的百分比，可以求得这次抽样调查中调查的学生总数；
（2）根据扇形统计图中的数据，可以计算出扇形统计图中“篮球”部分所对应的圆心角度数；
（3）根据（1）中的结果和条形统计图中的数据，可以计算出选择足球的人数，从而可以将条形统计图补充完整；
（4）根据统计图中的数据，由喜欢“跳绳”的人数所占百分比，可以计算出该校学生中喜欢“跳绳”的人数．
【详解】解：（1）8÷10%＝80（名），
即这次抽样调查中调查了80名学生，
故答案为：80；
（2）扇形统计图中“篮球”部分所对应的圆心角度数是：360°× SKIPIF 1 < 0 ＝108°，
故答案为：108°；
（3）选择足球的有：80×15%＝12（人），
补全的条形统计图如右图所示；
（4）该校学生中喜欢“跳绳”的约有2400× SKIPIF 1 < 0 ＝600（人），
故答案为：600．
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．
5．某市教育局为了了解初一学生第一学期参加社会实践活动的情况，随机抽查了本市部分初一学生第一学期参加社会实践活动的天数，并将得到的数据绘制成了下面两幅不完整的统计图．
请根据图中提供的信息，回答下列问题：
（1）扇形统计图中 a 的值为 ，该扇形圆心角的度数为 ；
（2）补全条形统计图；
（3）如果该市共有初一学生 20000 人，请你估计“活动时间不少于 5 天”的大约有多少人？
【答案】（1）25%；90°；（2）见解析；（3）15000人
【分析】（1）用1减去其他天数所占的百分比即可得到a的值，用360°乘以它所占的百分比，即可求出该扇形所对圆心角的度数；
（2）先求出参加社会实践活动的总人数，再乘以参加社会实践活动为6天的所占的百分比，求出参加社会实践活动为6天的人数，从而补全统计图；
（3）用总人数乘以活动时间不少于5天的人数所占的百分比即可求出答案．
【详解】解：（1）扇形统计图中a=1-30%-15%-10%-20%=25%，
该扇形所对圆心角的度数为360°×25%=90°；
故答案为：25%，90°；
（2）参加社会实践活动的总人数是： SKIPIF 1 < 0 （人），
则参加社会实践活动为6天的人数是：200×25%=50（人），
补图如下：
（3）该市初一学生第一学期社会实践活动时间不少于5天的人数约是：
20000×（30%+25%+20%）=15000（人）．
【点睛】本题考查了条形统计图、扇形统计图等知识，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
6．随着网络资源日趋丰富，更多人选择在线自主学习，在线学习方式有在线阅读、在线听课、在线答题、在线讨论．济川中学初二年级随机抽取部分学生进行“你对哪类在线学习方式最感兴趣”的调查(每位同学只能选一项)，并根据调查结果绘制成如下两幅不完整的统计图．根据图中信息，解答下列问题：
（1）补全条形统计图；
（2）求扇形统计图中“在线阅读”对应的扇形圆心角的度数．
【答案】（1）36，补图见解析；（2）96°
【分析】（1）根据在线答题的人数和所占的百分比可以求得本次调查的人数，然后即可得到在线听课的人数，从而可以将条形统计图补充完整；
（2）根据统计图中的数据，可以计算出扇形统计图中“在线阅读”对应的扇形圆心角的度数．
【详解】解：（1）本次调查的人数为：18÷20%=90，
在线听课的人数为：90-24-18-12=36，
补全的条形统计图如图所示；
（2）360°× SKIPIF 1 < 0 =96°，
即扇形统计图中“在线阅读”对应的扇形圆心角的度数是96°．
【点睛】本题考查条形统计图、扇形统计图，解答本题的关键是明确题意，利用数形结合的思想解答．
7．2020年11月20日，深圳第六次获得“全国文明城市”称号．“来了就是深圳人，来了就是志愿者”，如今深圳活跃了208万“红马甲”志愿者，共同服务深圳．某校随机抽取了部分学生对志愿服务活动情况进行如下调查：A．未参加过志愿服务活动；B．参加志愿服务活动1次；C．参加志愿服务活动2次；D．参加志愿服务活动3次及以上；并将调查结果绘制成了两幅不完整的统计图，请你根据图中提供的信息回答以下问题：
（1）共调查了 名学生；
（2）补全条形统计图；
（3）计算扇形统计图中“参加志愿服务活动2次”部分所对应的圆心角度数为 ；
（4）该校共有1200名学生，估计“参加志愿服务活动3次及以上”的学生大约有多少名？
【答案】（1）50；（2）见解析；（2）144°；（3）240
【分析】（1）用A的人数除以其对应百分比可得总人数，
（2）用总人数乘以30%，得出B的人数，再用总人数减去其它项人数求得D的人数即可补全图形；
（3）用360°乘以C的人数所占比例可得；
（4）总人数乘以样本中D的人数所占比例可得．
【详解】解：（1）这次被调查的学生共有5÷10%=50（名）；
（2）B的人数：50×30%=15（名）
D的人数：50-5-15-20=10（名）
补全条形统计图
（3） “参加志愿服务活动2次”部分所对应的圆心角度数为 SKIPIF 1 < 0
（4） SKIPIF 1 < 0 （名）
答：“参加志愿服务活动3次及以上”的学生大约有240名．
【点睛】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
8．为了了解某市学生中考体育选考项目情况，更好地进行课程安排．体育老师在全校随机抽取一部分 同学就“中考选考体育的体育项目”进行了一次抽样调查，下面是他通过收集的数据绘制的两幅不完整 的统计图，请你根据图中提供的信息，解答以下问题：
（1）体育老师共抽取 名学生；
（2）补全条形统计图；
（3）在扇形统计图中，“游泳”部分对应的圆心角的度数是
（4）若全校共 SKIPIF 1 < 0 名学生，请你估算“引体向上”部分的学生人数﹒
【答案】（1）50；（2）画图见解析；（3） SKIPIF 1 < 0 ；（4） SKIPIF 1 < 0 人
【分析】（1）根据球类运动的人数及占比即可求出抽取的总人数；
（2）用户总人数减去各组人数求出游泳部分的人数，故可补全统计图；
（3）用游泳部分的人数除以抽取的总人数即可求解；
（4）求出“引体向上”部分的占比即可求解﹒
【详解】 SKIPIF 1 < 0 （名）
故答案为：50；
SKIPIF 1 < 0 （人）
补全统计图如下：
SKIPIF 1 < 0
故答案为：72°；
SKIPIF 1 < 0 （人）
估算“引体向上”部分的学生人数为640人．
【点睛】考查条形统计图、扇形统计图的制作方法以及样本估计总体的统计方法，理清统计图中的数据之间的关系式解决问题的关键．
9．某校开设武术、舞蹈、剪纸三项活动课程，为了了解学生对这三项活动课程的兴趣情况，随机抽取了部分学生进行调查（每人从中只能选一顶），并将调查结果绘制成下面两幅统计图，请你结合图中信息解答问题．
（1）将条形统计图补充完整；
（2）本次抽样调查的样本容量是___；
（3）在扇形统计图中，计算女生喜欢剪纸活动课程人数对应的圆心角度数；
（4）已知该校有1200名学生，请结合数据简要分析该校学生对剪纸课程的兴趣情况．
【答案】（1）见解析；（2）100；（3）115.2°；（4）全校喜欢剪纸的学生360人
【分析】（1）根据扇形统计图可得出女生喜欢武术的占20%，利用条形图中喜欢武术的女生有10人，即可求出女生总人数，即可得出喜欢舞蹈的人数；
（2）根据（1）的计算结果再利用条形图即可得出样本容量；
（3）360°乘以女生中剪纸类人数所占百分比即可得；
（4）用全校学生数×喜欢剪纸的学生在样本中所占比例即可求出．
【详解】解：（1）被调查的女生人数为10÷20%＝50人，
则女生舞蹈类人数为50﹣（10+16）＝24人，
补全图形如下：
（2）样本容量为50+30+6+14＝100，
故答案为100；
（3）扇形图中剪纸类所占的圆心角度数为360°× SKIPIF 1 < 0 ＝115.2°；
（4）估计全校学生中喜欢剪纸的人数是1200× SKIPIF 1 < 0 ＝360，
全校喜欢剪纸的学生有360人．
【点睛】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
10．为了了解龙岗区学生喜欢球类活动的情况，采取抽样调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：
（1）本次共调查的学生人数为___，并把条形统计图补充完整；
（2）扇形统计图中m=___，n=___；
（3）表示“足球”的扇形的圆心角是___度；
（4）若龙岗区初中学生共有60000人，则喜欢乒乓球的有多少人．
【答案】（1）40，画图见解析；（2）10，20；（3）72；（4）24000人．
【分析】（1）根据喜欢篮球的有12人，所占的百分比是30%，据此即可求得总人数，然后利用总人数减去其它组的人数求得喜欢足球的人数，进而作出直方图；
（2）根据百分比的意义即可求解；
（3）利用360°乘以对应的百分比即可求解；
（4）利用总人数乘以对应的百分比即可求解．
【详解】解：（1）调查的总人数是：12÷30%=40（人），
则喜欢足球的人数是：40-4-12-16=8（人）．
．
故答案是：40；
（2）喜欢排球的所占的百分比是： SKIPIF 1 < 0 ×100%=10%，则m=10；
喜欢足球的所占的百分比是： SKIPIF 1 < 0 ×100%=20%，则n=20．
故答案为：10，20；
（3）表示足球的扇形的圆心角是：360°×20%=72°，
故答案为：72；
（4）龙岗区初中学生喜欢乒乓球的有60000×40%=24000（人）．
【点睛】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
11．保护环境，让我们从垃圾分类做起．某区环保部门为了提高宣传实效，抽样调查了部分居民小区一段时间内生活垃圾的分类情况（如图1），进行整理后，绘制了如下两幅尚不完整的统计图：
根据图表解答下列问题：
（1）请将图2﹣条形统计图补充完整；
（2）在图3﹣扇形统计图中，求出“D”部分所对应的圆心角等于 度；
（3）在抽样数据中，产生的有害垃圾共有 吨；
（4）调查发现，在可回收物中废纸垃圾约占 SKIPIF 1 < 0 ，若每回收1吨废纸可再造好红外线0.85吨．假设该城市每月产生的生活垃圾为10000吨，且全部分类处理，那么每月回收的废纸可再造好纸多少吨？
【答案】（1）见解析；（2）36（3）3（4）918（吨）．
【分析】（1）由统计图中的信息可知D类垃圾5吨，占总数的10%，由此可计算出垃圾的总量，结合统计图中的信息即可计算出ABC各类垃圾的吨数，并将条形统计图补充完整；
（2）由“D类垃圾占总数的10%”可得，扇形统计图中D类所对应的圆心角为：360°×10%=36°；
（3）由（1）中的计算结果可知在抽样数据中有害垃圾的数量；
（4）由题意可得：该城市每月回收的废纸可再造纸：10000×54%× SKIPIF 1 < 0 ×0.85（吨）．
【详解】（1）由题意可得该小区垃圾总量为：5÷10%=50（吨）；
∴A类垃圾有：50×54%=27（吨）；B类垃圾有：50×30%=15（吨）；
∴C类垃圾有：50-27-15-5=3（吨）；
由此，补充完整条形统计图如下：
（2）扇形统计图中，D类所对应的圆心角为：360°×10%=36°；
故答案为36
（3）由（1）中计算可知，在抽样数据中，有害垃圾有3吨；
故答案为3
（4）由题意可得，该城市每月回收的废纸可再造纸的数量为：10000×54%× SKIPIF 1 < 0 ×0.85=918（吨）．
答：该城市每月产生的生活垃圾回收的废纸可再造纸918吨．
12．某校为了了解七年级学生体育测试情况，以七年级（1）班学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制如下的统计图，请你结合图中所给的信息解答下列问题：
（说明：A级：90分~100分；B级：75分~89分；C级：60分~74分；D级：60分以下）
（1）请把条形统计图补充完整；
（2）扇形统计图中D级所在的扇形的圆心角度数是 ；
（3）若该校七年级有600名学生，请用样本估计体育测试中A级学生人数约为多少人？
【答案】（1）见解析（2）36°（3）120人
【分析】（1）根据A等人数为10人，占扇形图的20%，求出总人数，可以得出D的人数，即可画出条形统计图；
（2）根据D的人数即可得出所占百分比，进而得出所在的扇形的圆心角度数；
（3）利用总体人数与A组所占比例即可得出A级学生人数．
【详解】解：（1）总人数是：10÷20%＝50，则D级的人数是：50−10−23−12＝5．条形统计图补充如下：
（2）D级的学生人数占全班学生人数的百分比是：1−46%−20%−24%＝10%； D级所在的扇形的圆心角度数是360×10%＝36°；
（3）∵A级所占的百分比为20%，
∴A级的人数为：600×20%＝120（人）．
【点睛】本题主要考查了条形统计图、扇形图统计图以及用样本估计总体，利用图形获取正确信息以及扇形图与条形图相结合是解决问题的关键．
13．2019年深圳市创建文明城市期间，某区教育局为了了解全区中学生对课外体育运动项目的喜欢程度，随机抽取了某校八年级部分学生进行问卷调查（每人限选一种体育运动项目）.如图是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问题：

（1）这次活动一共调查了 名学生；
（2）在扇形统计图中，“跳绳”所在扇形圆心角等于 度；
（3）补全条形统计图；
（4）若该校有学生2000人， 请你估计该校喜欢“足球”的学生约有 .
【答案】（1）500；（2）36；（3）见解析；（4）400
【分析】（1）根据条形图可知选篮球的有200人，根据在扇形图中所占比例得出调查学生数；
（2）根据条形统计图中跳绳的人数和总人数，算出跳绳的比例，求出圆心角；
（3）根据总人数和选羽毛球所占的百分比，即可求出选羽毛球的人数，从而补全统计图；
（4）求出选足球的百分比，用该校的总人数乘以选足球的学生所占比例，即可求出该校喜欢足球的学生人数．
【详解】（1）根据题意得：
这次活动一共调查了：200÷40%=500（人）；
（2）“跳绳”所在扇形圆心角度数为50÷500×360°=36°；
（3）喜欢羽毛球的人数为：500×30%=150（人），补图如下：
（4）该校喜欢“足球”的学生约是：
2000×（1-40%-30%-10%）=400（人）.
【点睛】此题主要考查了条形图与扇形图的综合应用，根据图形得出正确信息，把两图形有机结合是解决问题的关键．
14．某校组织了“健康教育”手抄报征集活动，现从中抽取部分作品，按A、B、C、D四个等级进行奖励，并根据统计结果绘制了如下两幅不完整统计图.
（1）求抽取了多少份作品.
（2）被抽取作品中B等级有多少份？并补全条形统计图.
（3）扇形统计图中D等级所对的圆心角是多少度？
（4）若全校共征集到作品600份，请估计A作品有多少份？
【答案】(1)120(份);(2)48(份),详见解析;(3)18°;(4)180份.
【分析】(1)用C等级份数除以C等级所占的百分比，可得抽取的数量；
(2)用（1）中所求总份数减去A、C、D三等级数量即可得到B等级作品数，并补全统计图；
(3)先算出D等级所占总数的百分比,再乘以360°,即可算出度数.
(4)利用样本估计总体，将样本中A等级所占比例乘以600，可估计A等级数量．
【详解】(1)根据题意，共抽取作品30÷25%=120（份）；
(2)B等级作品数为：120﹣36﹣30﹣6=48（份），
补全条形统计图如图所示：
(3)6÷120=5%,360°×5%=18°.
(4)600× SKIPIF 1 < 0 =180，
答：若该校共征集到600份作品，估计等级为A的作品约有180份．
【点睛】本题考查统计的综合知识,关键在于通过图形得出有用信息.
15．某学校组织七年级学生参加了一次“运算能力”比赛，共有400名学生参加，参赛学生的成 SKIPIF 1 < 0 均为正数，且最低分为60分，为了解本次比赛学生的成绩分布情况，抽取了其中部分学生的成绩作为样本进行统计，并制作出了如下两个统计图：
请根据所给信息，解答下列问题：
（1）所抽取分析的学生数量为 人；
（2）成绩为 SKIPIF 1 < 0 这一组的人数占体体人数的百分比为 ；
（3）成绩为 SKIPIF 1 < 0 这一组的所在的扇形的圆心角度数为 ；
（4）请补全频数分布直方图；
（5）若成绩达到90分或以上为“优秀”等级，则参加这次比赛的学生中属于“优秀”等级的约有 人 .
【答案】（1）40；（2）15%；（3）72°；（4）见解析；（5）120人
【分析】（1）根据圆心角的度数可求出各个组所占的百分比，依据70≤x＜80这组的频数为8，占整体的20%，可求出样本容量，即调查的总人数，
(2)（3）根据调查总人数和各组的占比，可以求出每组的频数、频率，
（4）根据所求的结果，可补全频数分布直方图：
（5）求出样本中在90分及以上的“优秀”等级的占比，估计总体中“优秀”所占的百分比，进而求出“优秀”人数，
【详解】（1）54÷360＝0.15=15%，
360°×20%＝72°，
108÷360＝30%，
8÷20%＝40人，
40×30%＝12人，
40−6−8−12＝14人，
∴（1）所抽取分析的学生数量为40人，故填：40；
（2）成绩为 SKIPIF 1 < 0 这一组的人数占体体人数的百分比为15%，故填：15%；
（3）成绩为 SKIPIF 1 < 0 这一组的所在的扇形的圆心角度数为72°,故填：72° ；
（4）补全频数分布直方图如图所示：
（5）参加这次比赛的学生中属于“优秀”等级的约有400×30%＝120人，
故填：120．
【点睛】考查频数分布直方图和扇形统计图的制作方法，通过图表得到数据和数据之间的数量关系式解决问题的关键．
16．2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整)，已知A． B两组捐款人数的比为1:5.
被调查的捐款人数分组统计表：
请结合以上信息解答下列问题：
(1)求a的值和参与调查的总人数；
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数；
(3)已知该校有学生2200人，请估计捐款数不少于30元的学生人数有多少人?
【答案】（1）a=20，总人数为500人；（2）图详见解析，72°；（3）792人.
【分析】(1)根据a与100的比值是1：5，即可求得a的值，然后根据百分比的意义求得参与调查的总人数；
(2)根据百分比的意义求得C类的人数，即可补全统计图；根据B类人数占调查人数比例乘以周角可得圆心角度数；
(3)利用总人数2200乘以对应的百分比即可.
【详解】(1)依题意有a：100=1：5，
解得：a=20，
参与调查的总人数是：(20+100)÷(1-8%-28%-40%)=500；
(2)C类的人数是：500×40%=200(人)，
补图如图所示：
扇形B的圆心角度数为： SKIPIF 1 < 0 ×360°=72°；
(3)捐数值不少于30元的学生人数是：2200×(28%+8%)=792(人)，
答：捐数值不少于30元的学生约有792人．
【点睛】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
17．某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动，收集整理数据后，老师将减压方式分为五类，并绘制了如图①②两幅不完整的统计图，请根据图中的信息解答下列问题．
(1)九年级(1)班接受调查的学生共有多少名？
(2)补全条形统计图，并计算扇形统计图中的“体育活动C”所对应的圆心角度数．
【答案】(1)接受调查的学生有50名；(2)补全条形统计图见解析，“体育活动C”所对应的圆心角的度数为108°.
【分析】（1）利用“享受美食”的人数除以所占的百分比计算即可得解；(2)求出听音乐的人数即可补全条形统计图,由C的人数即可得到所对应的圆心角度数.
【详解】(1)接受调查的学生有10÷20%＝50(名)．
(2)听音乐的人数为50－10－5－15－8＝12(人)．
补全条形统计图如图：
“体育活动C”所对应的圆心角的度数＝ SKIPIF 1 < 0 ×360°＝108°.
【点睛】本题考查了条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
18．央视举办的《中国诗词大会》受到广大的关注.深圳某中学学生会就《中国诗词大会》节目的喜爱程度，在校内进行了问卷调查，并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级，分别记作A、B、C、D；根据调查结果绘制出如图所示的扇形和条形统计图，请结合图中所给信息解答下列问题：
（1）本次被调查的对象共有 人；被调查者“不太喜欢”有 人；
（2）将扇形统计图和条形统计图补充完整；
（3）假设这所学校有1500名学生，请据此估计“比较喜欢”的学生有多少人?
【答案】（1）50，5；（2）画图见解析；（3）600人
【分析】（1）从统计图中可以得到“喜欢”的有15人，占调查人数的30%，即可求出调查人数；调查人数乘以D组的百分比即可得到“不太喜欢”的人数；
（2）分别计算C组人数、百分比、D组人数、B组的百分比，即可补全统计图.
（3）用样本估计总体，样本中“比较喜欢”的占比40%；估计总体中“不太喜欢”的占比也是40%，然后计算即可.
【详解】解：（1）15÷30%=50人，50×10%=5人，故答案为：50，5；
（2）20÷50=40%，50-20-15-5=10人，10÷50=20%，补全统计图如图所示；
（3）1500×40%=600人，
答：该校1500名学生中“比较喜欢”的学生有600人.
【点睛】本题考查扇形统计图、条形统计图的意义和制法，从两个统计图中获取数量和数量之间的关系是解决问题的关键.
19．为了加强学生的安全意识，某校组织了学生参加安全知识竞赛，从中抽取了部分学生成绩进行统计，并按照成绩从低到高分成A，B，C，D，E五个小组，绘制统计图如下（未完成），解答下列问题：
（1）样本容量为______，频数分布直方图中 SKIPIF 1 < 0 ______；
（2）扇形统计图中D小组所对应的扇形圆心角为 SKIPIF 1 < 0 ，求n的值并补全频数分布直方图；
（3）若成绩在80分以上（不含80分）为优秀，全校共有2000名学生，估计成绩优秀的学生有多少名?
【答案】（1）200；16；（2） SKIPIF 1 < 0 ；补全频数分布直方图见解析；（3）估计成绩优秀的学生有940名．
【分析】（1）根据B组的频数以及百分比，即可求得总人数，然后根据百分比的意义求得a的值；
（2）利用360°乘以对应的百分比，即可求解；
（3）利用全校总人数乘以对应的百分比，即可求解．
【详解】（1）解：（1）学生总数是40÷20%＝200（人），
则a＝200×8%＝16；
故答案为：200；16；
（2） SKIPIF 1 < 0 ．
C组的人数是： SKIPIF 1 < 0 ．如图所示：
；
（3）样本D、E两组的百分数的和为 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 （名）
答：估计成绩优秀的学生有940名．
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
20．我校为了丰富学生课余生活，计划开设以下课外活动项目：A-篮球，B-乒乓球，C-羽毛球，D-足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查（每位学生必须选且只能选一个项目），并将调查结果绘制成了两幅统计图，请回答下列问题：
（1）这次被调查的学生共有______人，扇形统计图中，“D-足球”所占圆心角的度数是______ SKIPIF 1 < 0 ；
（2）请你将条形统计图补充完整；
（3）若该校学生总数为1000人，试估计该校学生中最喜欢“乒乓球”项目的人数．
【答案】（1）200，72°；（2）见详解；（3）400人
【分析】（1）根据统计图可得喜欢篮球的人数所占的百分比为10％，进而可得总数，然后问题可求解；
（2）由（1）及统计图可直接求解；
（3）先求出喜欢乒乓球的百分比，然后问题可求解．
【详解】解：（1）由统计图可得：
喜欢篮球的百分比为 SKIPIF 1 < 0 ，
∴被调查的学生共有20÷10％=200人，
∴喜欢足球的百分比为40÷200×100％=20％，
∴“D-足球”所占圆心角的度数为360°×20％=72°；
故答案为200，72°；
（2）由（1）及统计图可得：
喜欢“C-羽毛球”的人数为200-20-80-40=60人，
∴补全条形统计图如图所示：
（3）由（2）得：喜欢“B-乒乓球”的人数为80人，
∴“B-乒乓球”所占百分比为80÷200×100％=40％，
∴该校学生中最喜欢“乒乓球”项目的人数1000×40％=400人，
答：该校学生中最喜欢“乒乓球”项目的人数1000×40％=400人．
【点睛】本题主要考查条形统计图及扇形统计图，关键是根据统计图得到基本信息，然后进行求解即可．
组别
捐款额x/元
人数
A
1≤x＜10
a
B
10≤x＜20
100
C
20≤x＜30
______
D
30≤x＜40
______
E
40≤x
______