初中数学人教版（2024）七年级上册1.2.1 有理数教学ppt课件

这是一份初中数学人教版（2024）七年级上册1.2.1 有理数教学ppt课件，共32页。PPT课件主要包含了棋盘上的学问，×2×2，×2×2×2，×2×2×2×2，探究1，aa，aaa，个a相加可记为，n个a相加可记为，n个a相乘又可记为等内容，欢迎下载使用。
1. 理解有理数乘方的意义，了解幂、底数、指数等相关概念.2. 掌握有理数乘方的符号法则及相关性质，能够正确地进行有理数的乘方运算.
你认为国王的国库里有这么多米吗？
古时候，有个王国里有一位聪明的大臣，他发明了国际象棋，献给了国王，国王从此迷上了下棋. 为了对聪明的大臣表示感谢，国王答应满足这个大臣的一个要求. 大臣说：“就在这个棋盘上放一些米粒吧，第1格放1粒米，第2格放2粒米，第3格放4粒米，然后是8粒、16粒、32粒，…，一直到第64格.”“你真傻！就要这么一点米？” 国王哈哈大笑. 这位大臣说：“就怕您的国库里没有这么多米！”
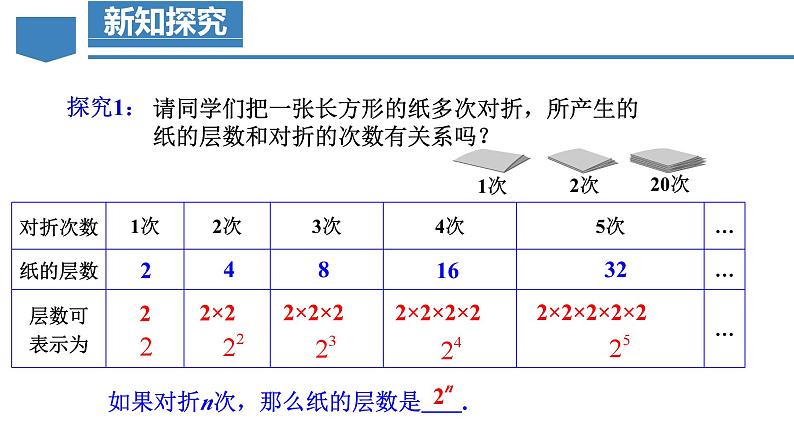
请同学们把一张长方形的纸多次对折，所产生的纸的层数和对折的次数有关系吗？
如果对折n次，那么纸的层数是 .
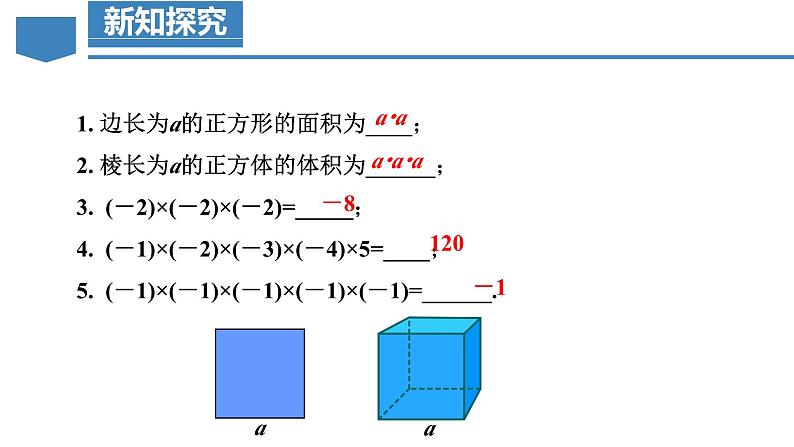
1. 边长为a的正方形的面积为____；2. 棱长为a的正方体的体积为______；3. (－2)×(－2)×(－2)=_____；4. (－1)×(－2)×(－3)×(－4)×5=____；5. (－1)×(－1)×(－1)×(－1)×(－1)=______.
边长为a的正方形的面积可记为：
棱长为a的正方体的体积可记为：
那么4个a相乘可记为：
2×2×2×2×2×2
一般地，n个相同的因数a相乘，记作an，读作“a的n次幂（或a的n次方）”，即
读作2的6次方（幂）.
读作2的4次方（幂）.
这种求n个相同因数的积的运算叫做乘方，乘方的结果叫做幂.
一个数可以看作这个数本身的一次方，例如8就是81，指数1通常省略不写.
a叫做底数，n叫做指数，an读作a的n次幂(或a的n次方).
1. 把下列乘法式子写成乘方的形式：（1）1×1×1×1×1×1×1=_______；（2）3×3×3×3×3=_______；（3）(－3)×(－3)×(－3)×(－3)=______；（4）
2. 把下列乘方写成乘法的形式：（1）(-9)3= __________________；（2） =___________；（3） = ___________ ；
思考：用乘方式子怎么表示33的相反数？
(1)(－5)2的底数是_____，指数是_____，(－5)2表示2个_____相乘，读作_____的2次方，也读作－5的_____.(2) 表示 个 相乘，读作 的 次方，也读作 的 次幂，其中 叫做 ，6叫做 .
温馨提示：幂的底数是分数或负数时，底数应该添上括号！
4. 判断下列各题是否正确：（1）23=2×3 ( ) （2）2+2+2=23 ( )（3） 23=2×2×2 ( )（4） -24=(-2)×(-2)×(-2)×(-2) ( )
(2)(-2)4 =(-2)×(-2)×(-2)×(-2)=16；
(3) 07 =0×0×0×0×0×0×0=0；
(1)(-4)3 =(-4)×(-4)×(-4)=-64；
与 结果相等吗？(2) 与 结果相等吗？
(1)负数的乘方，在书写时一定要把整个负数(连同符号)，用小括号括起来，这样便于辨认底数； (2)分数的乘方，在书写时一定要把整个分数用小括号括起来.
不计算下列各式，你能确定其结果的符号吗？从计算结果中，你能得到什么规律？
（1）(-2)51； （2）(-2)50； （3）250； （4）251；（5）(-1)2022；（6）(-1)2023；（7）02022；（8）12022．
归纳 (1) 正数的任何次幂是正数； (2) 负数的偶次幂是正数；负数的奇次幂是负数； (3) 0的任何次幂等于零； (4) 1的任何次幂等于1； (5) -1的偶次幂等于1；-1的奇次幂是-1．
(1)23中底数是 ，指数是 ，幂是 . 中底数是 ，指数是 ，幂是 .(3)(-5)4中底数是 ，指数是 ，幂是 . (4) 中底数是 ，指数是 ，结果是 .
2. 填空： 310的意义是 ，310 = .
(4) 　　　　　　　　　　　( )
3. 判断正误：(对的画“√”，错的画“×”)
(1) 32 =3×2=6. ( )
(2) (-2)3＝(-3)2. ( )
(3) -32=(-3)2. ( )
(5) ( )
(-2)3＝-8，(-3)2=9.
-32=-9，(-3)2=9.
-24=-2×2×2×2=-16.
例2：用计算器计算(-8)5和(-3)6.
所以(-8)5=-32768，(-3)6=729.
应用1：同学们，现在我们能解决本节课开始时《棋盘上的学问》中的问题吗？
1.84467×1019
估计每千颗米粒重40克，这么多颗米粒总重超过 亿吨.
7000
建议利用计算器帮助计算.
应用2：珠穆朗玛峰是世界最高峰，它的海拔高度是8844米. 把一张足够大的厚度为0.1毫米的纸，连续对折30次的厚度是多少？
这张纸对折30次后，厚度超过珠穆朗玛峰，是真的吗？
0.1×230 =107374182.4(mm)=107374(m) .
（1）（2）-23×(-32)（3）64÷(-2)5 （4）(-4)3÷(-1)200+2×(-3)4
（2）-23×(-32)=-8×(-9)=72；
（3）64÷(-2)5=64÷(-32)=-2；
（4）(-4)3÷(-1)200+2×(-3)4=-64÷1+2×81=98
思考：通过以上计算，对于乘除和乘方的混合运算，你觉得有怎样的运算顺序？
先算乘方，后算乘除；如果遇到括号就先进行括号里的运算.
(1)-(-3)2= ； (2)-32= ；
(3)(-5)3= ； (4)0.13= ；
(5)(-1)9= ； (6)(-1)12= ；
(7)(-1)2n= ； (8)(-1)2n+1= ；
(9)(-1)n= .
3. 对任意实数a，下列各式不一定成立的是（ ）
2. 在－|－3|3，－(－3)3，(－3)3，－33中，最大的数是(　　)
A. －|－3|3 B. －(－3)3 C. (－3)3 D. －33
A. a2=(－a)2 B. a3=(－a)3 C. |a|=|－a| D. a2≥0
1．（2022•广东）计算22的结果是（ ） A．1 B． C．2 D．4
【解答】解：22=4．故选：D．
2．（2022•西藏）已知a，b都是实数，若|a＋1|＋(b－2022)2=0，则ab= ．
【解答】解：因为|a＋1|＋(b－2022)2=0，所以a＋1=0，b－2022=0，即a=－1，b=2022，所以ab=(－1)2022=1，故答案为：1．
3．（2022•泸州）若(a－2)2＋| b＋3|=0，则ab= ．
【解答】解：由题意得，a－2=0，b＋3=0，解得a=2，b=－3，所以，ab=2×(－3)=－6．故答案为：－6．
1. 本节课学习的主要内容有哪些？这些内容体现了哪些数学思想方法？ 2. 有理数的乘方运算需要注意哪些事项？其运算步骤是什么？
1. 求几个相同因数的积的运算，叫做乘方.
2. 乘方的符号法则：
（1）正数的任何次幂都是正数
（2）负数的奇次幂是负数，负数的偶次幂是正数
（3）零的正整数次幂都是零
1. P47：习题1.5：第1、2、7题；2. P48：习题1.5：第12题；3. 课外思考： (1) 平方等于它本身的数是 ， 立方等于它本身的数是 .
(2) (+1)2022-(-1)2023 = .