

所属成套资源:沪科版数学七下同步讲义专项训练+培优练习(2份,原卷版+解析版)
沪科版数学七年级下册专题11.5 期末专项复习之选填压轴重难点题型(2份,原卷版+解析版)
展开
这是一份沪科版数学七年级下册专题11.5 期末专项复习之选填压轴重难点题型(2份,原卷版+解析版),文件包含沪科版数学七年级下册专题115期末专项复习之选填压轴重难点题型原卷版doc、沪科版数学七年级下册专题115期末专项复习之选填压轴重难点题型解析版doc等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。
【考点1 不等式组中的程序运算】
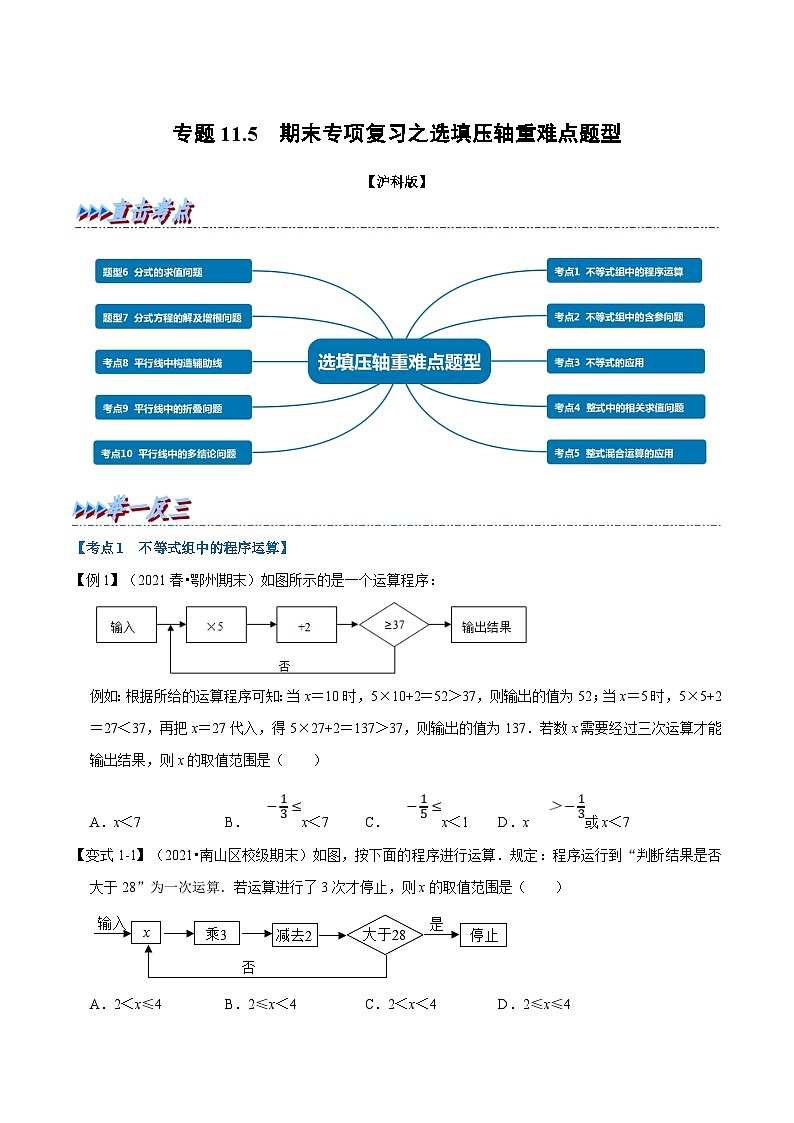
【例1】(2021春•鄂州期末)如图所示的是一个运算程序:
例如:根据所给的运算程序可知:当x=10时,5×10+2=52>37,则输出的值为52;当x=5时,5×5+2=27<37,再把x=27代入,得5×27+2=137>37,则输出的值为137.若数x需要经过三次运算才能输出结果,则x的取值范围是( )
A.x<7B.x<7C.x<1D.x或x<7
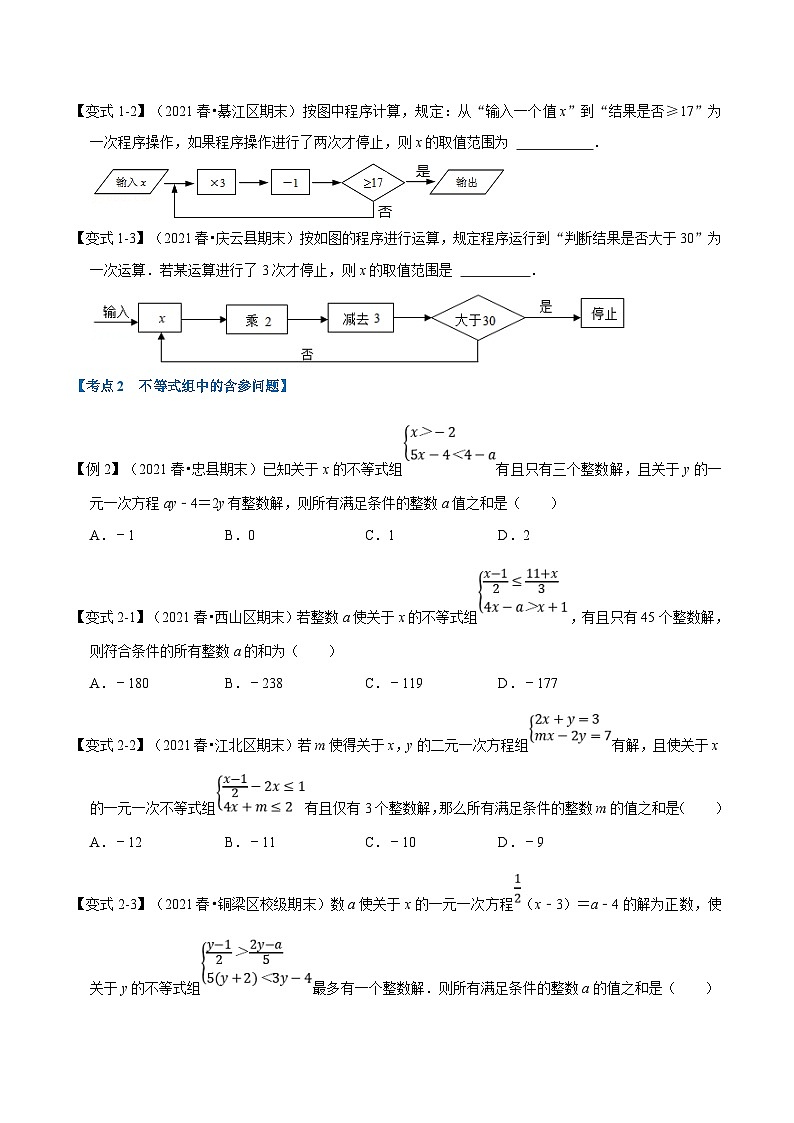
【变式1-1】(2021•南山区校级期末)如图,按下面的程序进行运算.规定:程序运行到“判断结果是否大于28”为一次运算.若运算进行了3次才停止,则x的取值范围是( )
A.2<x≤4B.2≤x<4C.2<x<4D.2≤x≤4
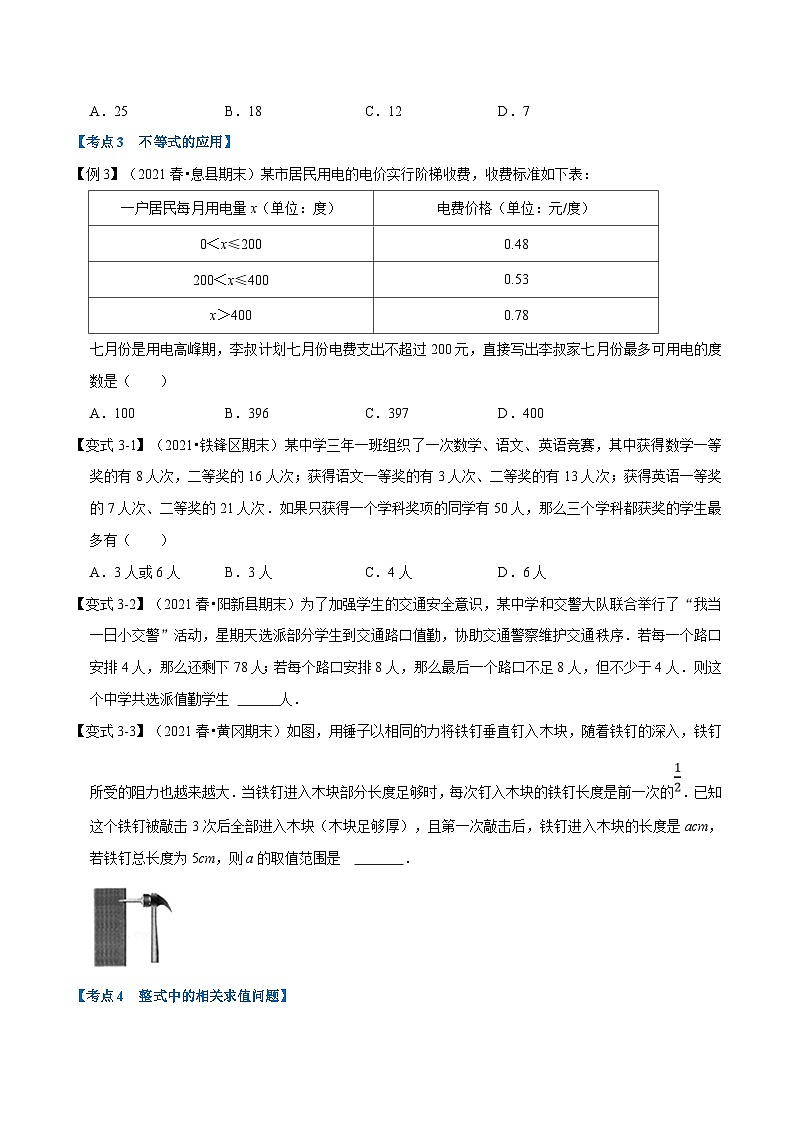
【变式1-2】(2021春•綦江区期末)按图中程序计算,规定:从“输入一个值x”到“结果是否≥17”为一次程序操作,如果程序操作进行了两次才停止,则x的取值范围为 .
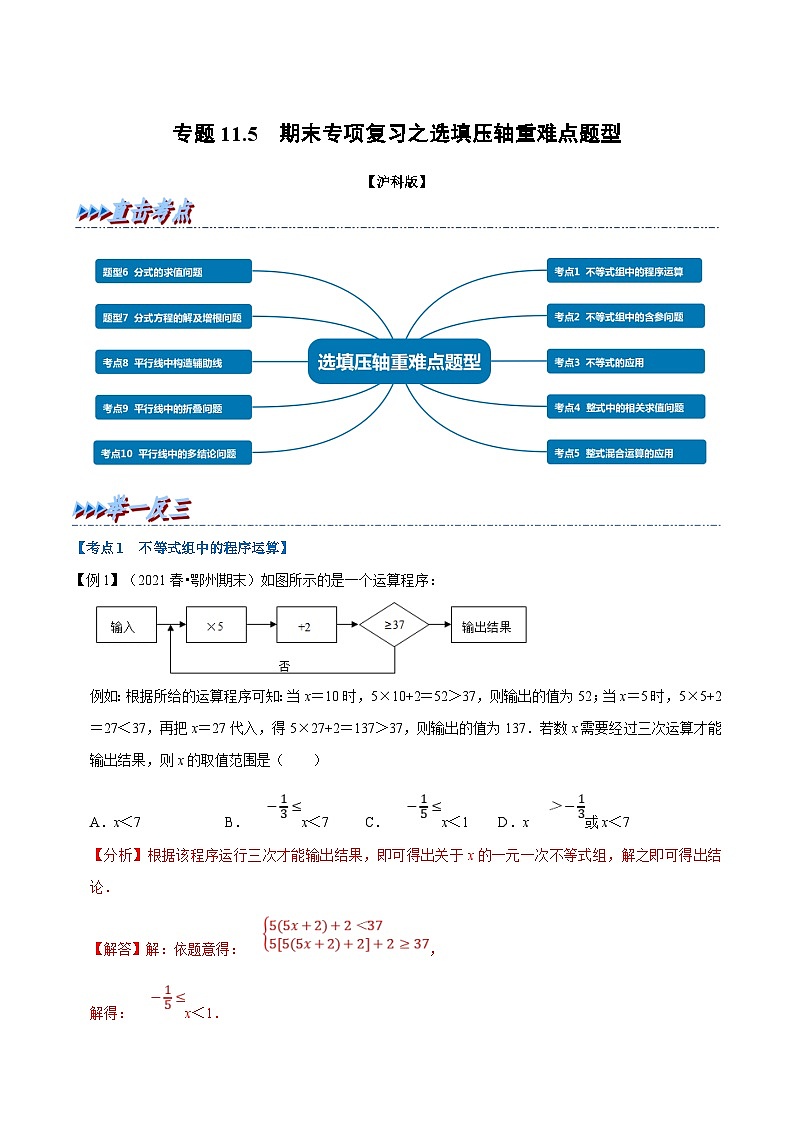
【变式1-3】(2021春•庆云县期末)按如图的程序进行运算,规定程序运行到“判断结果是否大于30”为一次运算.若某运算进行了3次才停止,则x的取值范围是 .
【考点2 不等式组中的含参问题】
【例2】(2021春•忠县期末)已知关于x的不等式组有且只有三个整数解,且关于y的一元一次方程ay﹣4=2y有整数解,则所有满足条件的整数a值之和是( )
A.﹣1B.0C.1D.2
【变式2-1】(2021春•西山区期末)若整数a使关于x的不等式组,有且只有45个整数解,则符合条件的所有整数a的和为( )
A.﹣180B.﹣238C.﹣119D.﹣177
【变式2-2】(2021春•江北区期末)若m使得关于x,y的二元一次方程组有解,且使关于x的一元一次不等式组有且仅有3个整数解,那么所有满足条件的整数m的值之和是( )
A.﹣12B.﹣11C.﹣10D.﹣9
【变式2-3】(2021春•铜梁区校级期末)数a使关于x的一元一次方程(x﹣3)=a﹣4的解为正数,使关于y的不等式组最多有一个整数解.则所有满足条件的整数a的值之和是( )
A.25B.18C.12D.7
【考点3 不等式的应用】
【例3】(2021春•息县期末)某市居民用电的电价实行阶梯收费,收费标准如下表:
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,直接写出李叔家七月份最多可用电的度数是( )
A.100B.396C.397D.400
【变式3-1】(2021•铁锋区期末)某中学三年一班组织了一次数学、语文、英语竞赛,其中获得数学一等奖的有8人次,二等奖的16人次;获得语文一等奖的有3人次、二等奖的有13人次;获得英语一等奖的7人次、二等奖的21人次.如果只获得一个学科奖项的同学有50人,那么三个学科都获奖的学生最多有( )
A.3人或6人B.3人C.4人D.6人
【变式3-2】(2021春•阳新县期末)为了加强学生的交通安全意识,某中学和交警大队联合举行了“我当一日小交警”活动,星期天选派部分学生到交通路口值勤,协助交通警察维护交通秩序.若每一个路口安排4人,那么还剩下78人;若每个路口安排8人,那么最后一个路口不足8人,但不少于4人.则这个中学共选派值勤学生 人.
【变式3-3】(2021春•黄冈期末)如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的.已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是acm,若铁钉总长度为5cm,则a的取值范围是 .
【考点4 整式中的相关求值问题】
【例4】(2021春•高新区期末)若m2=n+2021,n2=m+2021(m≠n),那么代数式m3﹣2mn+n3的值 .
【变式4-1】(2021春•高邮市校级期末)已知(2021﹣a)2+(a﹣2019)2=7,则代数式(2021﹣a)(a﹣2019)的值为 .
【变式4-2】(2021秋•仁寿县期末)已知a=2021x+2020,b=2021x+2021,c=2021x+2022,那么a2+b2+c2﹣ab﹣bc﹣ac的值等于 .
【变式4-3】(2021春•新都区期末)已知x2﹣3x+1=0,则x3﹣x2﹣5x+2021的值为 .
【考点5 整式混合运算的应用】
【例5】(2021春•泰兴市期末)4张长为m,宽为n(m>n)的长方形纸片,按如图的方式拼成一个边长为(m+n)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若3S1=2S2,则m,n满足的关系是( )
A.m=4.5nB.m=4nC.m=3.5nD.m=3n
【变式5-1】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A.abB.a=3bC.abD.a=4b
【变式5-2】(2021秋•邗江区期末)如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形ABCD,两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积S1与(2)图中长方形的面积S2的比是 .
【变式5-3】(2021春•姜堰区期末)如图,AB=5,C为线段AB上一点(AC<BC),分别以AC、BC为边向上作正方形ACDE和正方形BCFG,S△BEF﹣S△AEC,则S△BEC= .
【题型6 分式的求值问题】
【例6】(2021秋•弋江区期末)若,则的值为 .
【变式6-1】(2020秋•淮南期末)若ab=1,a﹣b=4,则 .
【变式6-2】(2021春•南开区期末)已知5a=2b=10,那么的值为 .
【变式6-3】(2021•宁波期末)若x、y、z满足3x+7y+z=1和4x+10y+z=2001,则分式的值为 .
【题型7 分式方程的解及增根问题】
【例7】(2021春•双流区期末)若关于x的一元一次不等式组的解集为x≥6,且关于y的分式方程的解是正整数,则所有满足条件的整数a的值之和是 .
【变式7-1】(2021春•锦江区期末)已知不等式组的解集为﹣1<x<1,且关于y的方程1的解为正数,则m的取值范围是 .
【变式7-2】(2021秋•高青县期末)如果关于x的分式方程的解为整数,且关于y的不等式组无解,则符合条件的所有负整数m的和为( )
A.﹣12B.﹣8C.﹣7D.﹣2
【变式7-3】(2021秋•渝中区校级期末)若关于x的不等式组无解,且关于y的分式方程有正整数解,则符合条件的所有整数a的和为( )
A.﹣2B.﹣1C.0D.1
【考点8 平行线中构造辅助线】
【例8】(2021春•碑林区校级期末)如图所示,已知AB∥EF,CD⊥BC于点C,若∠D=92°,则下列成立的是( )
A.∠E=20°B.∠E=∠BC.∠E﹣∠B=2°D.∠E+∠B=38°
【变式8-1】(2021春•新洲区期末)如图,直线k∥l,∠3﹣∠2=∠2﹣∠1=d>0.其中∠3<90°,∠1=40°,则∠4的最大整数值是( )
A.108°B.110°C.114°D.115°
【变式8-2】(2021春•浦江县期末)如图,AD∥BE,AC与BC相交于点C,且∠1∠DAB,∠2∠EBA.若∠C=45°,则n=( )
A.2B.3C.4D.5
【变式8-3】(2021春•焦作期末)已知AB∥CD,∠EAF∠EAB,∠ECF∠ECD,若∠E=66°,则∠F为( )
A.23°B.33°C.44°D.46°
【考点9 平行线中的折叠问题】
【例9】(2021春•嵊州市期末)如图,将长方形纸片沿EB,CF折叠成图1,使AB,CD在同一直线上,再沿BF折叠成图2,使点D落在点D'处,BD'交CF于点P,若∠CEB=37°,则∠CPB的度数为( )
A.110°B.111°C.112°D.113°
【变式9-1】(2021春•诸暨市期末)如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB、CD,若CD∥BE,且∠2=66°,则∠1的度数是( )
A.48°B.57°C.60°D.66°
【变式9-2】(2021春•庐山市 期末)如图,已知长方形纸片ABCD,点E,F在BC边上,点G,H在AD边上,分别沿EG,FH折叠,点B和点C恰好都落在点P处.若α+β=110°,则∠EPF的度数为( )
A.40°B.50°C.60°D.70°
【变式9-3】(2021春•零陵区期末)如图(1)所示为长方形纸带,将纸带沿EF折叠成图(2);再沿BF折叠成图(3);继续沿EF折叠成图(4)按此操作,最后一次折叠后恰好完全盖住∠EFG,整个过程共折叠了9次,问图(1)中∠DEF的度数是( )
A.20°B.19°C.18°D.15°
【考点10 平行线中的多结论问题】
【例10】(2021春•渝北区期末)如图,AB∥CD.OP⊥CD交AB于点P.交CD于点O,OF平分∠AOD,OE⊥OF,∠BAO=50°,有下列结论:①∠AOF=65°;②∠AOE=∠COE;③∠POF=∠COE;④∠AOP=2∠COE.其中正确的结论有( )
A.①②③④B.①②③C.①③④D.①②④
【变式10-1】(2021春•北碚区校级期末)如图,AB∥CD,点E,P在直线AB上(P在E的右侧),点G在直线CD上,EF⊥FG,垂足为F,M为线段EF上的一动点,连接GP,GM,∠FGP与∠APG的角平分线交于点Q,且点Q在直线AB,CD之间的区域,下列结论:
①∠AEF+∠CGF=90°
②∠AEF+2∠PQG=270°
③若∠MGF=2∠CGF,则3∠AEF+∠MGC=270°
④若∠MGF=n∠CGF,则∠AEF∠MGC=90°
正确的个数是( )
A.4B.3C.2D.1
【变式10-2】(2021春•荷塘区期末)①如图1,AB∥CD,则∠A+∠E+∠C=180°;②如图2,AB∥CD,则∠P=∠A﹣∠C;③如图3,AB∥CD,则∠E=∠A+∠1;④如图4,直线AB∥CD∥EF,点O在直线EF上,则∠α﹣∠β+∠γ=180°.以上结论正确的个数是( )
A.1个B.2个C.3个D.4个
【变式10-3】(2021秋•嵩县期末)如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:
①BC平分∠ABG;
②AC∥BG;
③与∠DBE互余的角有2个;
④若∠A=α,则∠BDF=180°.
其中正确的是 .(请把正确结论的序号都填上)
一户居民每月用电量x(单位:度)
电费价格(单位:元/度)
0<x≤200
0.48
200<x≤400
0.53
x>400
0.78
相关试卷
这是一份沪科版数学七年级下册专题11.6 期末专项复习之大题压轴重难点题型(2份,原卷版+解析版),文件包含沪科版数学七年级下册专题116期末专项复习之大题压轴重难点题型原卷版doc、沪科版数学七年级下册专题116期末专项复习之大题压轴重难点题型解析版doc等2份试卷配套教学资源,其中试卷共69页, 欢迎下载使用。
这是一份沪科版七年级数学下册举一反三系列专题11.8期末复习之选填压轴题专项训练特训(原卷版+解析),共49页。
这是一份沪科版七年级数学下册精品特训专题11.8期末复习之选填压轴题专项训练(原卷版+解析),共49页。









