北师大版数学七年级下册同步课时练习2.3.1 平行线的性质（含解析）

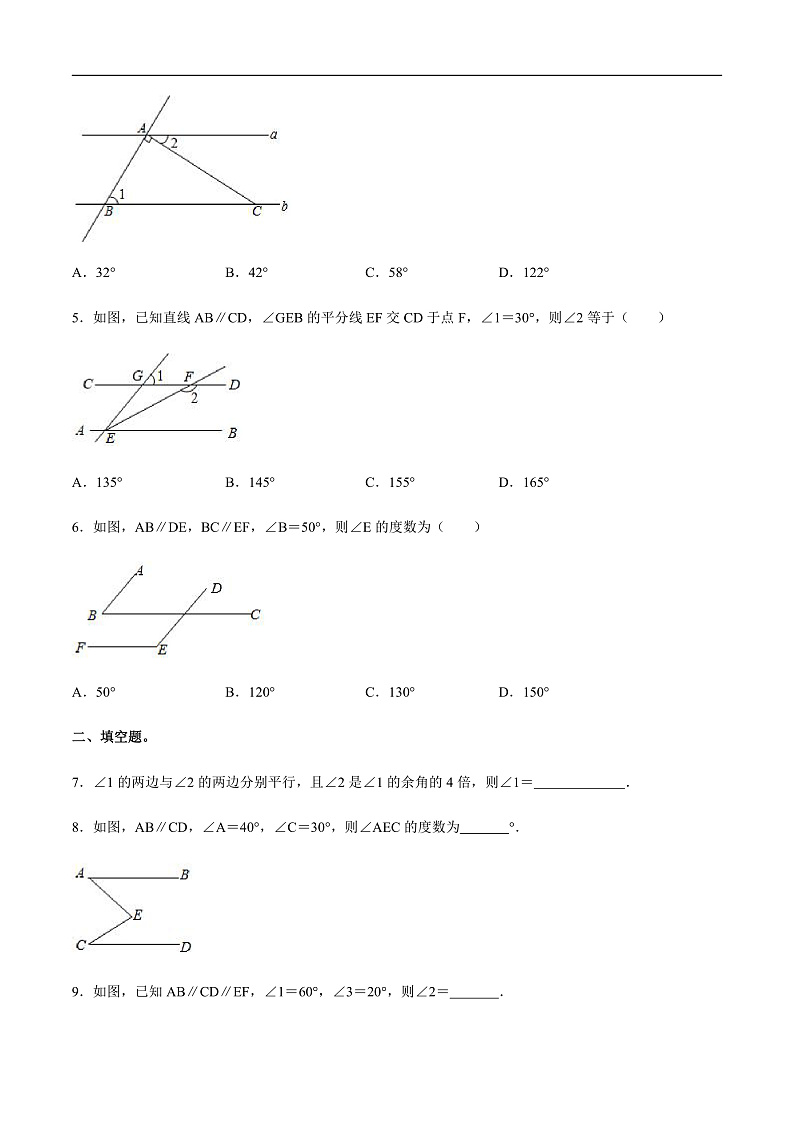
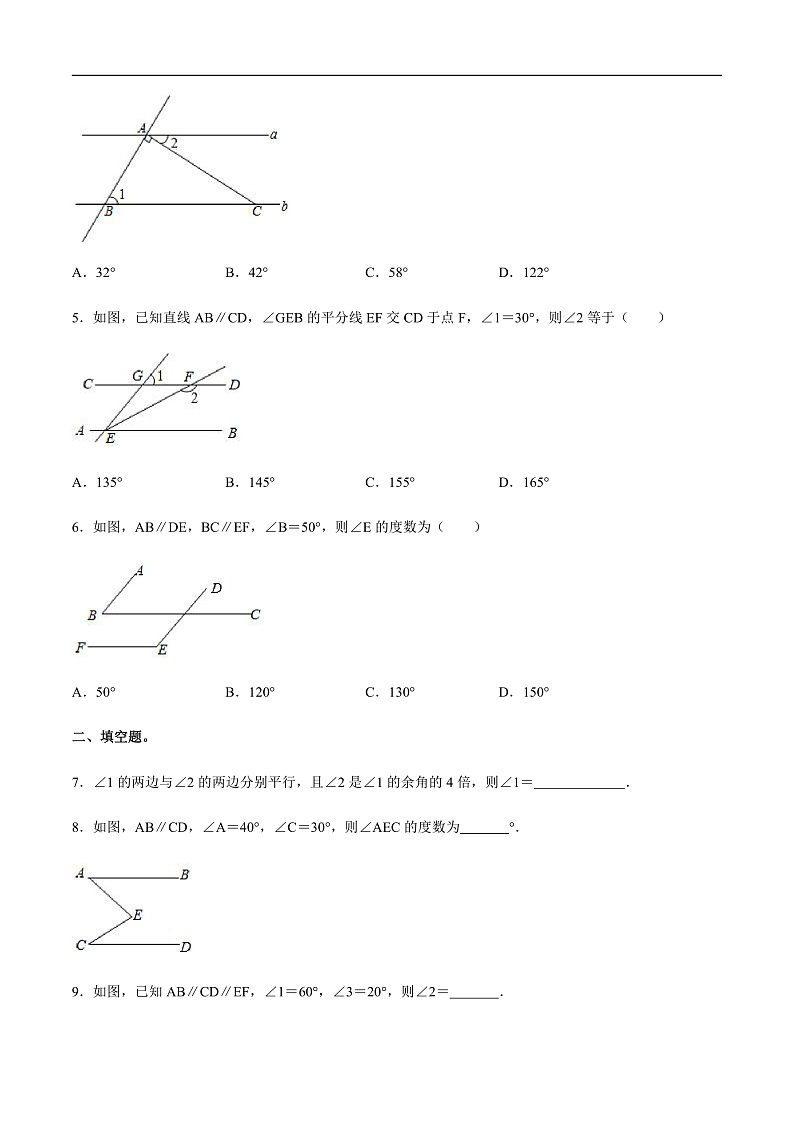
2.3.1 平行线的性质一、选择题。1．一副三角板如图摆放，且AB∥CD，则∠1的度数为（　　）A．80° B．60° C．105° D．75°2．如图，AB∥CD，∠1＝65°，∠2＝35°，则∠B＝（　　）A．20° B．25° C．30° D．35°3．如图，将直尺与含30°角的直角三角板叠放在一起，若∠1＝140°，则∠2的度数是（　　）A．105° B．100° C．110° D．120°4．如图，直线a∥b，直线c与直线a，b分别交于A，B两点，AC⊥AB于点A，交直线b于点C，如果∠1＝58°，那么∠2的度数为（　　）A．32° B．42° C．58° D．122°5．如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1＝30°，则∠2等于（　　）A．135° B．145° C．155° D．165°6．如图，AB∥DE，BC∥EF，∠B＝50°，则∠E的度数为（　　）A．50° B．120° C．130° D．150°二、填空题。7．∠1的两边与∠2的两边分别平行，且∠2是∠1的余角的4倍，则∠1＝　 　．8．如图，AB∥CD，∠A＝40°，∠C＝30°，则∠AEC的度数为　 °．9．如图，已知AB∥CD∥EF，∠1＝60°，∠3＝20°，则∠2＝　 　．10．如图，把一张长方形纸片ABCD沿EF折叠后，点C，D分别落在C'，D'的位置上，EC'交AD于点G．已知∠EFG＝58°，那么∠BEG＝　 　度．11．已知∠MON＝40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O重合），连接AC交射线OE于点D，设∠OAC＝x°，若AB∥ON，当x＝　 　时，使得△ADB中有两个相等的角．三、解答题。12．如图，AB∥CD，DA⊥AC，垂足为A，若∠ADC＝35°，求∠1的度数．13．如图，AE∥CF，∠A＝∠C．（1）若∠1＝35°，求∠2的度数；（2）判断AD与BC的位置关系，并说明理由．14．已知AM∥CN，点B为平面内一点，AB⊥BC于点B．（1）如图1，直接写出∠A和∠C之间的数量关系是　 　；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD＝∠C．2.3.1 平行线的性质参考答案与试题解析一、选择题。1．一副三角板如图摆放，且AB∥CD，则∠1的度数为（　　）A．80° B．60° C．105° D．75°【解答】解：如图所示，∵AB∥CD，∠D＝45°∴∠AEF＝∠D＝45°，∵∠1＝∠AEF+∠EAF，∠EAF＝30°，∴∠1＝∠45°+30°＝75°．故选：D．2．如图，AB∥CD，∠1＝65°，∠2＝35°，则∠B＝（　　）A．20° B．25° C．30° D．35°【解答】解：∵AB∥CD，∠1＝65°，∴∠AEG＝∠1＝65°，∵∠2＝35°，∠2＝∠EFB，∴∠EFB＝35°，∵∠AEG＝∠B+∠EFB，∴∠B＝65°﹣35°＝30°，故选：C．3．如图，将直尺与含30°角的直角三角板叠放在一起，若∠1＝140°，则∠2的度数是（　　）A．105° B．100° C．110° D．120°【解答】解：如图，解：∵AB∥CD，∠1＝140°，∴∠3＝∠1＝140°，∴∠4＝∠3﹣30°＝110°，∴∠2＝∠4＝110°，故选：C．4．如图，直线a∥b，直线c与直线a，b分别交于A，B两点，AC⊥AB于点A，交直线b于点C，如果∠1＝58°，那么∠2的度数为（　　）A．32° B．42° C．58° D．122°【解答】解：如图：∵直线a∥b，∴∠1+∠BAD＝180°，∵AC⊥AB于点A，∠1＝58°，∴∠2＝180°﹣90°﹣58°＝32°，故选：A．5．如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1＝30°，则∠2等于（　　）A．135° B．145° C．155° D．165°【解答】解：∵AB∥CD，∴∠GEB＝∠1＝30°，∵EF为∠GEB的平分线，∴∠FEB＝∠GEB＝15°，∴∠2＝180°﹣∠FEB＝165°．故选：D．6．如图，AB∥DE，BC∥EF，∠B＝50°，则∠E的度数为（　　）A．50° B．120° C．130° D．150°【解答】解：∵AB∥DE，∴∠1＝∠B＝50°，∵BC∥EF，∴∠E＝180°﹣∠1＝180°﹣50°＝130°．故选：C．二、填空题。7．∠1的两边与∠2的两边分别平行，且∠2是∠1的余角的4倍，则∠1＝　72°或60°　．【解答】解：如图所示，∵∠1与∠2的两边分别平行，∴∠1＝∠2或∠+∠2＝180°，∵∠2是∠1余角的4倍，∴∠2＝4（90°﹣∠1），（1）当∠1＝∠2时，∠1＝4（90°﹣∠1），∴∠1＝360°﹣4∠1，∴∠1＝72°．（2）∠1+∠2＝180°，∴∠1+4（90°﹣∠1）＝180°，∴360°﹣3∠1＝180°，∴∠1＝60°．故答案为：72°或60°8．如图，AB∥CD，∠A＝40°，∠C＝30°，则∠AEC的度数为　70　°．【解答】解：如图，作EF∥AB．∵AB∥EF，AB∥CD，∴EF∥CD，∴∠A＝∠AEF，∠C＝∠CEF，∴∠AEC＝∠AEF+∠CEF＝∠A+∠C＝40°+30°＝70°，故答案为70．9．如图，已知AB∥CD∥EF，∠1＝60°，∠3＝20°，则∠2＝　140°　．【解答】解：如图，∵AB∥EF，∴∠AEF＝∠1，∵∠1＝60°，∴∠AEF＝60°，∵∠3＝20°，∴∠CEF＝60°﹣20°＝40°，∵CD∥EF，∴∠2+∠CEF＝180°，∴∠2＝180°﹣40°＝140°．故答案为：140°．10．如图，把一张长方形纸片ABCD沿EF折叠后，点C，D分别落在C'，D'的位置上，EC'交AD于点G．已知∠EFG＝58°，那么∠BEG＝　64　度．【解答】解：∵AD∥BC，∴∠CEF＝∠EFG＝58°，由折叠的性质得：∠GEF＝∠CEF＝58°，∴∠BEG＝180°﹣∠GEF﹣∠CEF＝64°．故答案为：64．11．已知∠MON＝40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O重合），连接AC交射线OE于点D，设∠OAC＝x°，若AB∥ON，当x＝　120°或60°　时，使得△ADB中有两个相等的角．【解答】解：∵∠MON＝40°，OE平分∠MON，∴∠AOB＝∠BON＝20°，∵AB∥ON，∴∠ABO＝20°，①∠BAD＝∠ABD时，∵∠BAD＝∠ABD，∴∠BAD＝20°，∵∠AOB+∠ABO+∠OAB＝180°，∴∠OAB＝140°，∴∠OAC＝120°；②∠BAD＝∠BDA时，∵∠BAD＝∠BDA，∠ABO＝20°，∴∠BAD＝80°，∵∠AOB+∠ABO+∠OAB＝180°，∴∠OAC＝60°；故答案为：120°或60°．三、解答题。12．如图，AB∥CD，DA⊥AC，垂足为A，若∠ADC＝35°，求∠1的度数．【解答】解：∵AB∥CD，∴∠BAD＝∠ADC＝35°，∵DA⊥AC，∴∠EAD＝90°，∴∠1＝∠EAD﹣∠BAD＝90°﹣35°＝55°．13．如图，AE∥CF，∠A＝∠C．（1）若∠1＝35°，求∠2的度数；（2）判断AD与BC的位置关系，并说明理由．【解答】解：（1）∵AE∥CF，∴∠BDC＝∠1＝35°，又∵∠2+∠BDC＝180°，∴∠2＝180°﹣∠BDC＝180°﹣35°＝145°；（2）BC∥AD．理由：∵AE∥CF，∴∠A+∠ADC＝180°，又∵∠A＝∠C，∴∠C+∠ADC＝180°，∴BC∥AD．14．已知AM∥CN，点B为平面内一点，AB⊥BC于点B．（1）如图1，直接写出∠A和∠C之间的数量关系是　∠A+∠BCN＝90°　；（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD＝∠C．【解答】解：（1）如图1，AM与BC的交点记作点O，∵AM∥CN，∴∠BCN＝∠AOB，∵AB⊥BC，∴∠A+∠AOB＝90°，∴∠A+∠BCN＝90°，故答案为：∠A+∠BCN＝90°；（2）如图2，过点B作BG∥DM，∵BD⊥AM，∴DB⊥BG，即∠ABD+∠ABG＝90°，又∵AB⊥BC，∴∠CBG+∠ABG＝90°，∴∠ABD＝∠CBG，∵AM∥CN，BG∥AM，∴CN∥BG，∴∠C＝∠CBG，∴∠ABD＝∠C．