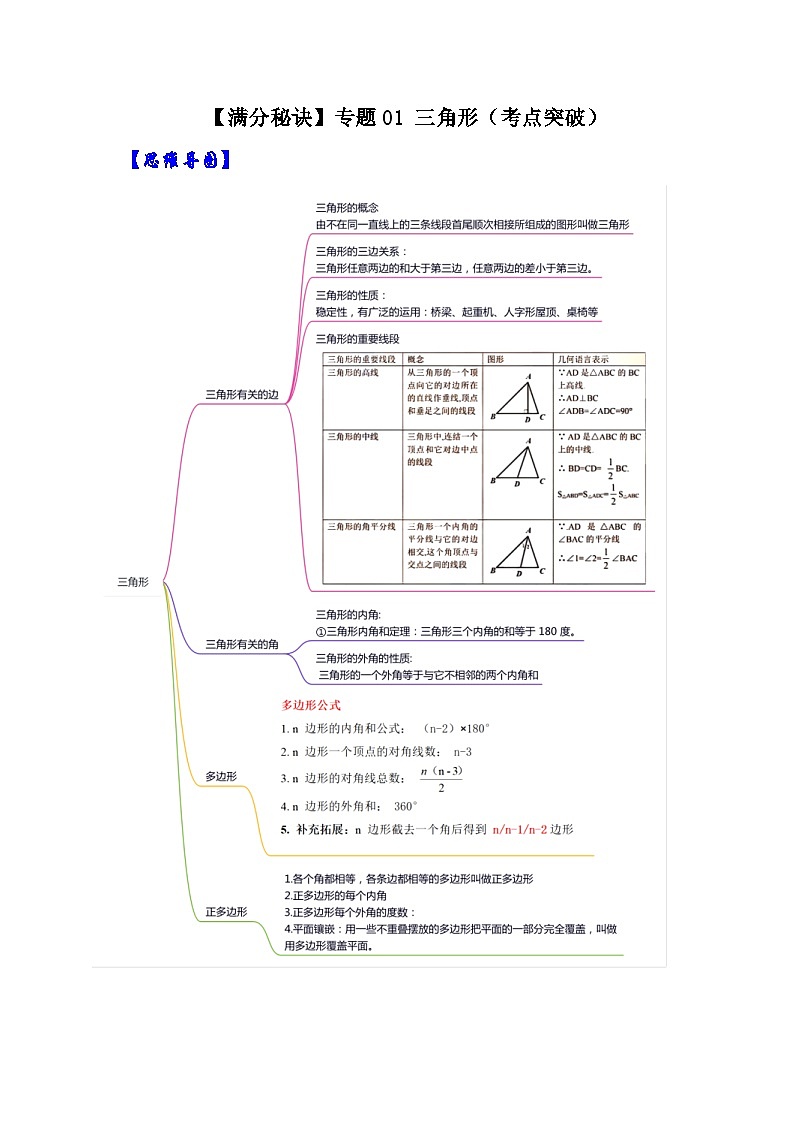
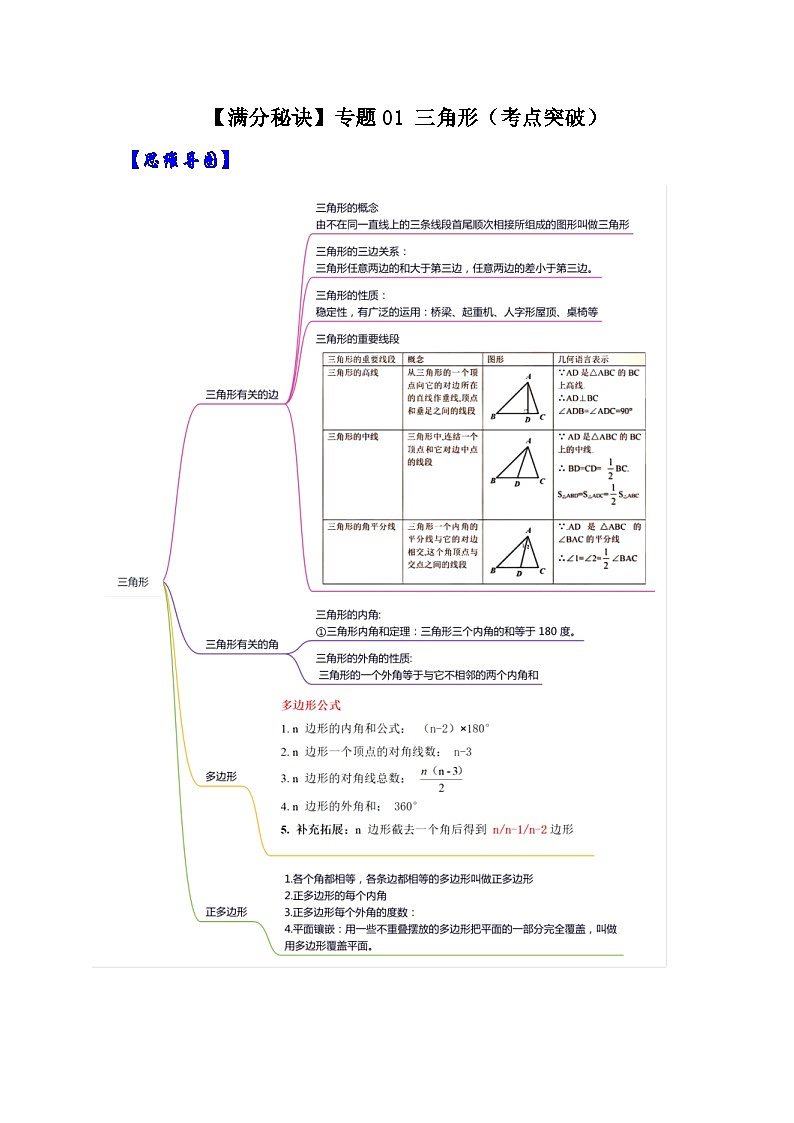
人教版数学八年级上册期末提升练习专题01 三角形（考点突破）（2份，原卷版+解析版）

这是一份人教版数学八年级上册期末提升练习专题01 三角形（考点突破）（2份，原卷版+解析版），文件包含人教版数学八年级上册期末提升练习专题01三角形考点突破原卷版doc、人教版数学八年级上册期末提升练习专题01三角形考点突破解析版doc等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。

【常见考法】

【真题分点透练】
【考点1 三角形三边关系】
1．（2021秋•桃江县期末）从长为9，6，5，4的4条线段中任取3条线段，不能构成三角形的是（ ）
A．9，6，5B．9，6，4C．9，5，4D．6，5，4
【答案】C
【解答】解：从这4条线段中任取3条，总的情况有4种：
（9，6，5），（9，6，4），（6，5，4），（9，5，4），
其中所取3条线段不能构成一个三角形的情况只有一种：（9，5，4），
故选：C．
2．（2021秋•南宁期末）下列长度的线段中，能组成三角形的是（ ）
A．4，6，8B．1，2，4C．5，6，12D．2，3，5
【答案】A
【解答】解：根据三角形任意两边的和大于第三边，得
A．4+6＞8，故能组成三角形；
B．1+2＜4，故不能组成三角形；
C．5+6＜12，故不能组成三角形；
D．2+3＝5，故不能组成三角形．
故选：A．
3．（2022春•永年区校级期末）已知三角形的三边长为4，x，6．若x是整数，则x的值不可能是（ ）
A．10B．4C．6D．8
【答案】A
【解答】解：∵三角形的三边长分别为4，x，6，
∴第三边的取值范围为：2＜x＜10，
∵x为整数，
∴x的值不可能是10．
故选：A．
4．（2022春•巴中期末）如图，为估计池塘岸边A、B两点的距离，小明在池塘的一侧选取一点O，测得OA＝10米，OB＝8米，A、B间的距离不可能是（ ）
A．12米B．10米C．20米D．8米
【答案】C
【解答】解：∵10﹣8＜AB＜10+8，
∴2＜AB＜18，
∴不可能是20米．
故选：C．
5．（2022春•榆树市期末）如图，在△ABC中，AD是BC边上的中线，△ABD的周长比△ADC的周长多1，AB与AC的和为11．
（1）求AB、AC的长；
（2）求BC边的取值范围．
【解答】解：（1）∵AD是BC边上的中线，
∴BD＝CD，
∴△ABD的周长﹣△ADC的周长＝（AB+AD+BD）﹣（AC+AD+CD）＝AB﹣AC＝1，
即AB﹣AC＝2①，
又AB+AC＝11②，
①+②得．2AB＝12，
解得AB＝6，
②﹣①得，2AC＝10，
解得AC＝5，
∴AB和AC的长分别为：AB＝6，AC＝5；
（2）∵AB＝6，AC＝5，
∴1＜BC＜11．
6．（2022春•嵩县期末）已知a，b，c是一个三角形的三边长，
（1）填入“＞、＜或＝”号：a﹣b﹣c 0，b﹣a﹣c 0，c+b﹣a 0．
（2）化简：|a﹣b﹣c|+|b﹣a﹣c|﹣|c+b﹣a|．
【解答】解：（1）∵a，b，c是一个三角形的三边长，
∴a﹣b﹣c＜0，b﹣a﹣c＜0，c+b﹣a＞0．
故答案为：＜，＜，＞；
（2）原式＝b+c﹣a+a+c﹣b﹣c﹣b+a
＝a﹣b+c．
【考点2 三角形性质】
7.（2022春•沐川县期末）如图，人字梯中间一般会设计一“拉杆”，以增加使用梯子时的安全性，这样做蕴含的道理是（ ）
A．三角形具有稳定性
B．三角形内角和等于180°
C．两点之间线段最短
D．同位角相等，两直线平行拉杆
【答案】A
【解答】解：人字梯中间一般会设计一“拉杆”，以增加使用梯子时的安全性，这样做的道理是三角形具有稳定性．
故选：A
【考点3 三角形角平分线、中线和高】
8．（2021秋•梁平区期末）下列四个图形中，线段BE是△ABC中AC边上的高的图形是（ ）
A．B．
C．D．
【答案】C
【解答】解：A、线段BE不是△ABC中AC边上的高，故本选项不符合题意；
B、线段BE不是△ABC中AC边上的高，故本选项不符合题意；
C、线段BE是△ABC中AC边上的高，本选项符合题意；
D、线段BE不是△ABC中AC边上的高，故本选项不符合题意；
故选：C．
9．（2022春•昭通期末）下列说法中正确的是（ ）
A．三角形的三条中线必交于一点
B．直角三角形只有一条高
C．三角形的中线可能在三角形的外部
D．三角形的高线都在三角形的内部
【答案】A
【解答】解：A、三角形的三条中线必交于一点，本选项说法正确，符合题意；
B、直角三角形有三条高，故本选项说法错误，不符合题意；
C、三角形的中线不可能在三角形的外部，故本选项说法错误，不符合题意；
D、三角形的高线不一定都在三角形的内部，故本选项说法错误，不符合题意；
故选：A．
10．（2021秋•汇川区期末）如图，AD，AE，AF分别是△ABC的中线，角平分线，高，下列各式中错误的是（ ）
A．BC＝2CDB．∠BAE＝∠BAC
C．∠AFB＝90°D．AE＝CE
【答案】D
【解答】解：∵AD，AE，AF分别是△ABC的中线，角平分线，高，
∴BC＝2BD＝2DC，∠BAE＝∠CAE＝∠BAC，∠AFB＝∠AFC＝90°，
故选项A、B、C正确，选项D错误，
故选：D．
【考点4 三角形面积】
11．（2021秋•江夏区校级月考）如图，在△ABC中，AB＝2，BC＝4，△ABC的高AD与CE的比是多少？（提示：利用三角形的面积公式）
【解答】解：S△ABC＝AB•CE＝BC•AD，
∵AB＝2cm，BC＝4cm，
∴×2•CE＝×4•AD，
∴＝．
【考点5 三角形内角和定理】
12．（2022春•广饶县期末）如图，在△ABC中，BF平分∠ABC，CF平分∠ACB，∠BFC＝125°，则∠A的度数为（ ）
A．60°B．80°C．70°D．45°
【答案】C
【解答】解：在△FBC中，∠BFC＝125°．
∴∠FBC+∠FCB＝180°﹣∠BFC＝55°．
∵BF平分∠ABC，CF平分∠ACB．
∴∠ABC＝2∠FBC，∠ACB＝2∠FCB．
∴∠ABC+∠ACB＝2（∠FBC+∠FCB）＝110°．
∴在△ABC中，∠A＝180°﹣（∠ABC+∠ACB）＝70°．
故选：C．
13．（2022春•栾城区期末）如图，点D、E为ABC边BC、AC上的两点，将△ABC沿线段DE折叠，点C落在
BD上的C'处，若∠C＝30°，则∠AEC′＝（ ）
A．60°B．58°C．45°D．43°
【答案】A
【解答】解：由折叠的性质知：∠C＝∠C′＝30°．
∴∠AEC′＝∠C+∠C′＝60°．
故选：A．
14．（2022春•海南期末）如图，在△ABC中，D是AB上一点，E是AC上一点，BE、CD相交于点F，∠A＝61°，∠ACD＝37°，∠ABE＝18°．
（1）求∠BDC的度数；
（2）求∠BFD的度数．
【解答】解：（1）∵∠BDC＝∠A+∠ACD，
∴∠BDC＝61°+37°＝98°；
（2）∵∠BFD+∠BDC+∠ABE＝180°，
∴∠BFD＝180°﹣∠BDC﹣∠ABE
＝180°﹣98°﹣18°
＝64°．
15．（2022春•六盘水期末）如图，在△ABC中，若∠1＝∠2，DE∥BC．
（1）试说明FG∥BE；
（2）若BE为∠ABC的角平分线，∠2＝30°，∠C＝50°，求∠A的度数．
【解答】解：（1）∵DE∥BC，
∴∠2＝∠EBC．
又∵∠1＝∠2，
∴∠EBC＝∠1．
∴FG∥BE．
（2）由（1）得，∠EBC＝∠2＝30°．
∵BE为∠ABC的角平分线，
∴∠ABC＝2∠EBC＝60°．
∴∠A＝180°﹣∠ABC﹣∠C＝70°．
16．（2022春•漳州期末）如图，在△ABC中，CD是AB边上的高，CE平分∠ACB．若∠ACB＝80°，∠A比∠B大20°，求∠DCE的度数．
【解答】解：∵CE平分∠ACB，∠ACB＝80°，
∴，∠A+∠B＝180°﹣80°＝100°．
∵∠A比∠B大20°，
∴∠A﹣∠B＝20°，
∴∠A＝60°，∠B＝40°，
∵CD是AB边上的高，
∴∠CDA＝90°，
∴∠ACD＝90°﹣∠A＝30°，
∴∠DCE＝∠ACE﹣∠ACD
＝40°﹣30°
＝10°．
【考点6 三角形外角性质】
17．（2022春•香坊区校级期末）如图，在△ABC中，AD平分∠BAC，∠B＝65°，∠C＝35°，则∠ADB的度数为（ ）
A．55°B．65°C．75°D．85°
【答案】C
【解答】解：在△ABC中，AD平分∠BAC，∠B＝65°，∠C＝35°，
∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣65°﹣35°＝80°，
∴∠CAD＝，
∴∠ADB＝∠C+∠CAD＝35°+40°＝75°，
故选：C．
18．（2022春•永年区校级期末）在△ABC中，∠A，∠B，∠C的三个外角度数的比为4：5：6，则∠A＝（ ）
A．96°B．84°C．48°D．24°
【答案】B
【解答】解：设∠A、∠B、∠C的三个外角度数分别为4x、5x、6x，
则4x+5x+6x＝360°，
解得，x＝24°，
则∠A的外角为4x＝96°，
∴∠A＝84°，
故选：B．
19．（2022春•泗水县期末）如图，CE是△ABC的外角∠ACD的平分线，若∠B＝30°，∠ACE＝60°，则∠A＝（ ）
A．60°B．100°C．90°D．80°
【答案】C
【解答】解：∵CE平分∠ACD，∠ACE＝60°，
∴∠ACD＝2∠ACE＝120°，
∵∠ACD是△ABC的外角，∠B＝30°，
∴∠ACD＝∠A+∠B，
∴∠A＝∠ACD﹣∠B＝90°．
故选：C．
20．（2022春•新泰市期末）如图，在△ABC中，∠B＝50°，AE是∠BAC的平分线，外角∠ACD＝100°，则∠AEC的度数为（ ）
A．65°B．70°C．75°D．50°
【答案】C
【解答】解：∵∠B＝50°，∠ACD＝100°，
∴∠BAC＝50°，
∵AE是∠BAC的平分线，
∴∠EAC＝25°，
∴∠AEC＝∠ACD﹣∠EAC＝100°﹣25°＝75°，
故选：C．
21．（2022春•光明区期末）某零件的形状如图所示，按照要求∠B＝20°，∠BCD＝110°，∠D＝30°，那么∠A的度数是（ ）
A．50°B．60°C．70°D．80°
【答案】B
【解答】解：延长DC交AB于E，
∵∠BCD＝∠B+∠CEB，∠BCD＝110°，∠B＝20°，
∴∠CEB＝110°﹣20°＝90°，
∵∠CEB＝∠A+∠D，∠D＝30°，
∴∠A＝90°﹣30°＝60°，
故选：B．
【考点7 直角三角形性质】
22．（2022春•巴中期末）如图，在△ABC中，∠C＝90°，顶点B在直线PQ上，顶点A在直线MN上，BC平分∠PBA，AC平分∠MAB．
（1）求证：PQ∥MN；
（2）求∠QBC+∠NAC的度数．
【解答】（1）证明：∵∠C＝90°，
∴∠CBA+∠CAB＝90°，
∵BC平分∠PBA，AC平分∠MAB，
∴∠PBA＝2∠CBA，∠MAB＝2∠CAB，
∴∠PBA+∠MAB＝180°，
∴PQ∥MN；
（2）解：∵∠CBA+∠CAB＝90°，∠PBA+∠MAB＝180°，
∴∠QBC+∠NAC＝∠CBA+∠CAB+∠PBA+∠MAB＝90°+180°＝270°．
23．（2022春•邓州市期末）如图，在△ABC中，∠BAC＝90°，AD⊥BC于点D，BE平分∠ABC，AD、BE相交于点F．
（1）若∠CAD＝36°，求∠AEF的度数；
（2）试说明：∠AEF＝∠AFE．
【解答】（1）解：∵AD⊥BC，
∴∠ABD+∠BAD＝90°，
∵∠BAC＝90°，
∴∠BAD+∠CAD＝90°，
∴∠ABD＝∠CAD＝36°，
∵BE平分∠ABC，
∴∠ABE＝∠ABC＝18°，
∴∠AEF＝90°﹣∠ABE＝72°；
（2）证明：∵BE平分∠ABC，
∴∠ABE＝∠CBE，
∵∠ABE+∠AEF＝90°，∠CBE+∠BFD＝90°，
∴∠AEF＝∠BFD，
∵∠AFE＝∠BFD，
∴∠AEF＝∠AFE．
【考点8 多边形的外交角和内角】
24．（2021秋•巩义市期末）一个正多边形，它的一个内角恰好是一个外角的5倍，则这个正多边形的边数是（ ）
A．十二B．十一C．十D．九
【答案】A
【解答】解：设这个正多边形一个外角是x°，由题意得：
5x+x＝180，
∴x＝30，
∴这个正多边形的边数是360°÷30°＝12．
故选：A．
25．（2022春•东坡区期末）如图，是有一个公共顶点O的两个全等正五边形，若将它们的其中一边都放在直线a上，则∠AOB的度数为（ ）
A．108°B．120°C．135°D．144°
【答案】A
【解答】解：如图．
由题意得，∠1＝∠2＝72°，∠4＝∠5＝108°．
∴∠3＝180°﹣∠1﹣∠2＝36°．
∴∠AOB＝360°﹣∠4﹣∠5﹣∠3＝108°．
故选：A．
26．（2022春•淮安区期末）一个多边形的每个外角都是45°，则这个多边形的边数为（ ）
A．八B．九C．十D．七
【答案】A
【解答】解：∵360÷45＝8（边），
∴多边形的边数为八，
故选：A．
27．（2022春•古县期末）为了求n边形内角和，下面是老师与同学们从n边形的一个顶点引出的对角线把n边形划分为若干个三角形，然后得出n边形的内角和公式．这种数学的推理方式是（ ）
A．归纳推理B．数形结合C．公理化D．演绎推理
【答案】A
【解答】解：探究多边形内角和公式时，从n边形的一个顶点出发引出（n﹣3）条对角线，将n边形分割成（n﹣2）个三角形，这（n﹣2）个三角形的所有内角之和即为n边形的内角和，这一探究过程运用的数学思想是归纳推理思想，
故选：A．
38．（2022春•单县期末）若一个多边形的一个内角为144°，则这个图形为正（ ）边形．
A．十一B．十C．九D．八
【答案】B
【解答】解：设这个正多边形的边数为n，
∴（n﹣2）×180°＝144°×n，
∴n＝10．
故选：B．
29．（2022春•井研县期末）如图，大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α，再沿直线前进8米，到达点C后，又向左旋转α角度，照这样走下去，第一次回到出发地点时，他共走了72米，则每次旋转的角度α为（ ）
A．30°B．40°C．45°D．60°
【答案】B
【解答】解：∵72÷8＝9，
∴360°÷9＝40°．
∴每次旋转的角度α＝40°．
故选：B．
30．（2022春•衢江区期末）如图，在四边形ABCD中，∠C＝110°，与∠BAD，∠ABC相邻的外角都是120°，则∠α的值为（ ）
A．50°B．55°C．60°D．65°
【答案】A
【解答】解：∵在四边形ABCD中，∠C＝110°，
∴∠C相邻的外角度数为：180°﹣110°＝70°，
∴∠α＝360°﹣70°﹣120°﹣120°＝50°．
故选：A．
31．（2022春•宽城县期末）如图，五边形ABCDE中，∠B＝80°，∠C＝110°，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，则∠1+∠2+∠3等于（ ）
A．90°B．190°C．210°D．180°
【答案】B
【解答】解：延长AB，DC，
∵∠B＝80°，
∴∠4＝100°，
∵∠C＝110°，
∴∠5＝70°，
∴∠4+∠5＝170°，
根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5＝360°，
∴∠1+∠2+∠3＝360°﹣170°＝190°．
故选：B．
32．（2022春•芝罘区期末）如图，几条线段首尾顺次连接，∠D＝28°，则∠A+∠B+∠C+∠E的度数为（ ）
A．180°B．208°C．178°D．152°
【答案】B
【解答】解：∵如图可知∠BGD＝∠C+∠B，∠GFE＝∠E+∠A，
又∵∠BGD＝∠D+∠GFD，
∴∠B+∠C＝∠D+∠GFD，
又∵∠GFE+∠GFD＝180°，
∴∠E+∠A+∠B+∠C﹣∠D＝180°，
又∵∠D＝28°，
∴∠A+∠B+∠C+∠E＝180°+28°＝208°．
故选：B．
33．（2022春•长安区期末）一个多边形边数每增加1条时，其内角和（ ）
A．增加180°B．增加360°C．不变D．不能确定
【答案】A
【解答】解：∵n边形的内角和＝（n﹣2）×180°，
∴多边形的边数增加1，其内角和增加180°，
故选：A．
34．（2022春•定远县期末）五边形ABCDE中，∠A+∠B+∠E＝300°，如图，DP、CP分别平分∠EDC、∠BCD，则∠P＝（ ）
A．45°B．60°C．90°D．120°
【答案】B
【解答】解：∵在五边形ABCDE中，∠A+∠B+∠E＝300°，
∴∠EDC+∠BCD＝（5﹣2）×180°﹣300°＝240°，
又∵DP、CP分别平分∠EDC、∠BCD，
∴∠PDC+∠PCD＝120°，
∴△CDP中，∠P＝180°﹣（∠PDC+∠PCD）＝180°﹣120°＝60°．
故答案为：B．
35．（2022春•菏泽期末）一个正多边形的内角和是它的外角和的3倍，则这个多边形的边数是（ ）
A．8B．9C．7D．6
【答案】A
【解答】解：设这个多边形的边数为x．
由题意得，180°（x﹣2）＝360°×3．
∴x＝8．
故选：A．
36．（2022春•新化县期末）一个多边形，它的内角和比外角和的4倍多180°，则这个多边形的边数是（ ）
A．9B．10C．11D．12
【答案】C
【解答】解：根据题意，得
（n﹣2）•180°＝360°×4+180°，
解得：n＝11．
则这个多边形的边数是11．
故选：C．
37．（2021秋•碑林区校级期末）如图，∠A+∠B+∠C+∠D+∠E等于（ ）
A．90°B．120°C．180°D．360°
【答案】C
【解答】解：如图，连接BC，
∵∠D+∠E+∠EFD＝180°，∠FBC+∠FCB+∠BFC＝180°，∠DFE＝∠BFC，
∴∠D+∠E＝∠FBC+∠FCB，
∴∠A+∠ABE+∠ACD+∠D+∠E
＝∠A+∠ABE+∠ACD+∠FBC+∠FCB
＝∠A+∠ABC+∠ACB
＝180°，
故选：C．
38．（2018秋•南昌县期中）如图，五边形ABCDE的各内角都相等，且∠1＝∠2，∠3＝∠4，求x的值．
【解答】解：因为五边形的内角和是540°，
则每个内角为540°÷5＝108°，
∴∠E＝∠C＝108°，
又∵∠1＝∠2，∠3＝∠4，由三角形内角和定理可知，
∠1＝∠2＝∠3＝∠4＝（180°﹣108°）÷2＝36°，
∴x＝∠EDC﹣∠1﹣∠3＝108°﹣36°﹣36°＝36°．
39．（2019秋•天心区期末）如图，在四边形ABCD中，∠A＝∠C＝90°，BE平分∠ABC，DF平分∠CDA．
（1）若∠ABC＝76°，求∠AEB的大小；
（2）求证：BE∥DF．
【解答】（1）解：∵∠ABC＝76°，BE平分∠ABC，
∴＝38°，
∴∠AEB＝180°﹣∠A﹣∠ABE＝180°﹣90°﹣38°＝52°；
（2）证明：∵∠A＝∠C＝90°，
∴∠ABC+∠ADC＝180°，
∵BE平分∠ABC，DF平分∠ADC，
∴∠ABE＝∠CBE＝∠ABC，∠ADF＝∠CDF＝∠ADC，
∴∠ABE+∠ADF＝（∠ABC+∠ADC）＝×180°＝90°，
又∠ABE+∠AEB＝90°，
∴∠ADF＝∠AEB，
∴BE∥DF．
40．（2021秋•虎林市校级期末）已知一个多边形的每一个内角都比它相邻的外角的4倍多30°，求这个多边形是几边形？并求出这个多边形的内角和．
【解答】解：设外角为x°，
由题意得：x+4x+30＝180，
解得：x＝30，
360°÷30°＝12，
∴（12−2）×180＝1800°，
∴这个多边形的内角和是1800°，是十二边形．
41．（2022春•定远县期末）如图，在四边形ABCD中，∠B+∠ADC＝180°，CE平分∠BCD交AB于点E，连接DE．
（1）若∠A＝50°，∠B＝85°，求∠BEC的度数；
（2）若∠A＝∠1，求证：∠CDE＝∠DCE．
【解答】（1）解：∵∠B+∠ADC＝180°，∠A+∠B+∠BCD+∠ADC＝360°，
∴∠A+∠BCD＝180°，
∵∠A＝50°，
∴∠BCD＝130°，
∵CE平分∠BCD，
∴∠BCE＝∠BCD＝65°，
∵∠B＝85°，
∴∠BEC＝180°﹣∠BCE﹣∠B＝180°﹣65°﹣85°＝30°；
（2）证明：∵由（1）知：∠A+∠BCD＝180°，
∴∠A+∠BCE+∠DCE＝180°，
∵∠CDE+∠DCE+∠1＝180°，∠1＝∠A，
∴∠BCE＝∠CDE，
∵CE平分∠BCD，
∴∠DCE＝∠BCE，
∴∠CDE＝∠DCE．
【考点9作图】
42．（2022春•如东县期末）如图，在△ABC中，∠ABC＝∠ACB＝2∠A，BD是边AC上的高．
（1）依题意补全图形；
（2）求∠DBC的度数．
【解答】解：（1）如图，线段BD即为所求；
（2）∵∠ABC＝∠ACB＝2∠A，
又∵∠ABC+∠ACB+∠A＝180°，
∴5∠A＝180°，
∴∠A＝36°，
∴∠C＝2∠A＝72°，
∵BD⊥AC，
∴∠BDC＝90°，
∴∠DBC＝90°﹣72°＝18°．
【考点10方向角】
43．（2016秋•黄梅县校级期末）如图，B处在A处的南偏西45°方向，C处在A处的南偏东15°方向，C处在B处的北偏东80°方向，求∠ACB的度数．
【解答】解：如图，根据方向角的定义，可得∠BAE＝45°，∠CAE＝15°，∠DBC＝80°．
∵∠BAE＝45°，∠EAC＝15°，
∴∠BAC＝∠BAE+∠EAC＝45°+15°＝60°．
∵AE，DB是正南正北方向，
∴BD∥AE，
∵∠DBA＝∠BAE＝45°，
又∵∠DBC＝80°，
∴∠ABC＝80°﹣45°＝35°，
∴∠ACB＝180°﹣∠ABC﹣∠BAC＝180°﹣60°﹣35°＝85°．