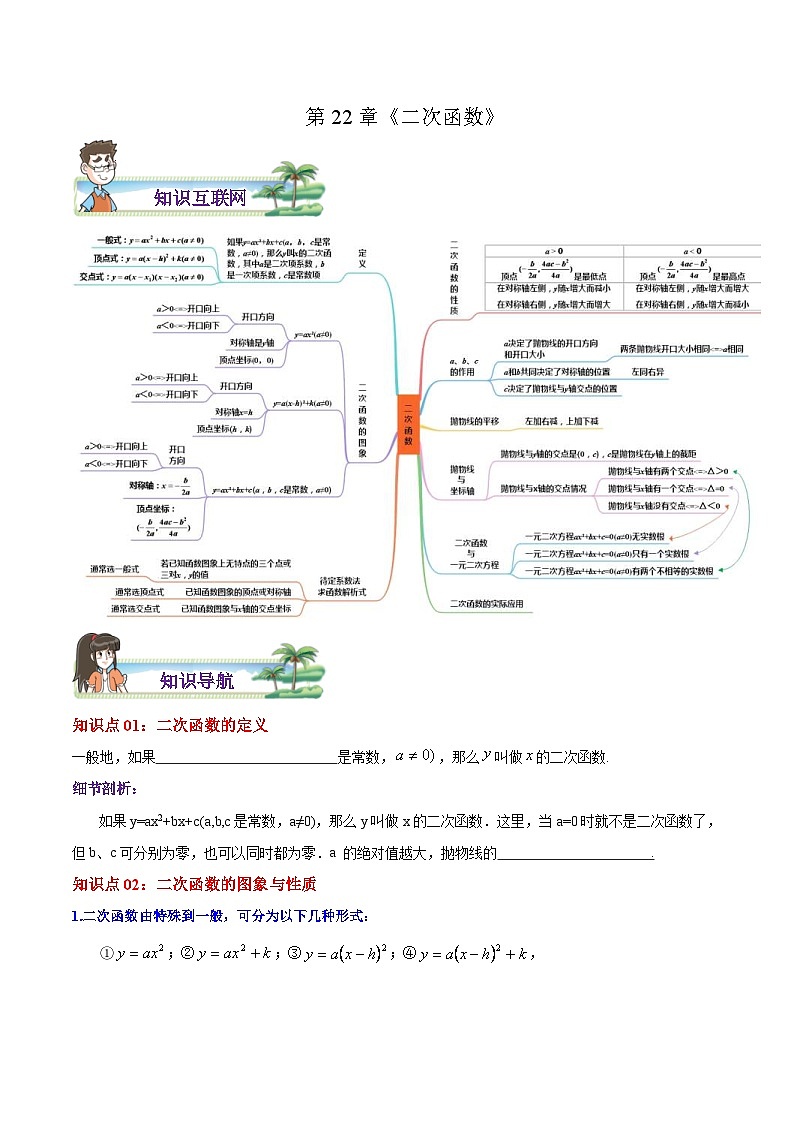
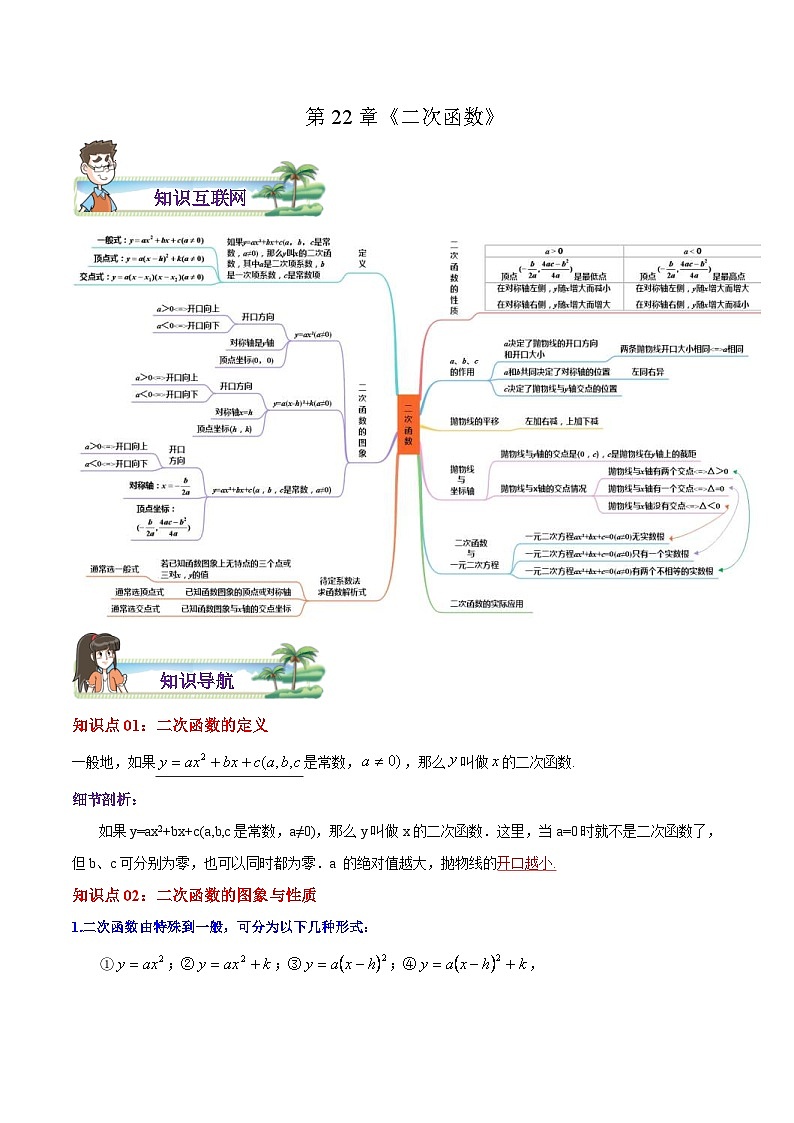
人教版数学九年级上册期末章节重难点复习讲义第22章 二次函数（2份，原卷版+解析版）

这是一份人教版数学九年级上册期末章节重难点复习讲义第22章 二次函数（2份，原卷版+解析版），文件包含人教版数学九年级上册期末章节重难点复习讲义第22章二次函数原卷版doc、人教版数学九年级上册期末章节重难点复习讲义第22章二次函数解析版doc等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。

知识导航
知识点01：二次函数的定义
一般地，如果 是常数，，那么叫做的二次函数.
细节剖析：
如果y=ax2+bx+c(a,b,c是常数，a≠0)，那么y叫做x的二次函数．这里，当a=0时就不是二次函数了，但b、c可分别为零，也可以同时都为零．a 的绝对值越大，抛物线的 .
知识点02：二次函数的图象与性质
1.二次函数由特殊到一般，可分为以下几种形式：
①；②；③；④，
其中；⑤.（以上式子a≠0）
几种特殊的二次函数的图象特征如下：
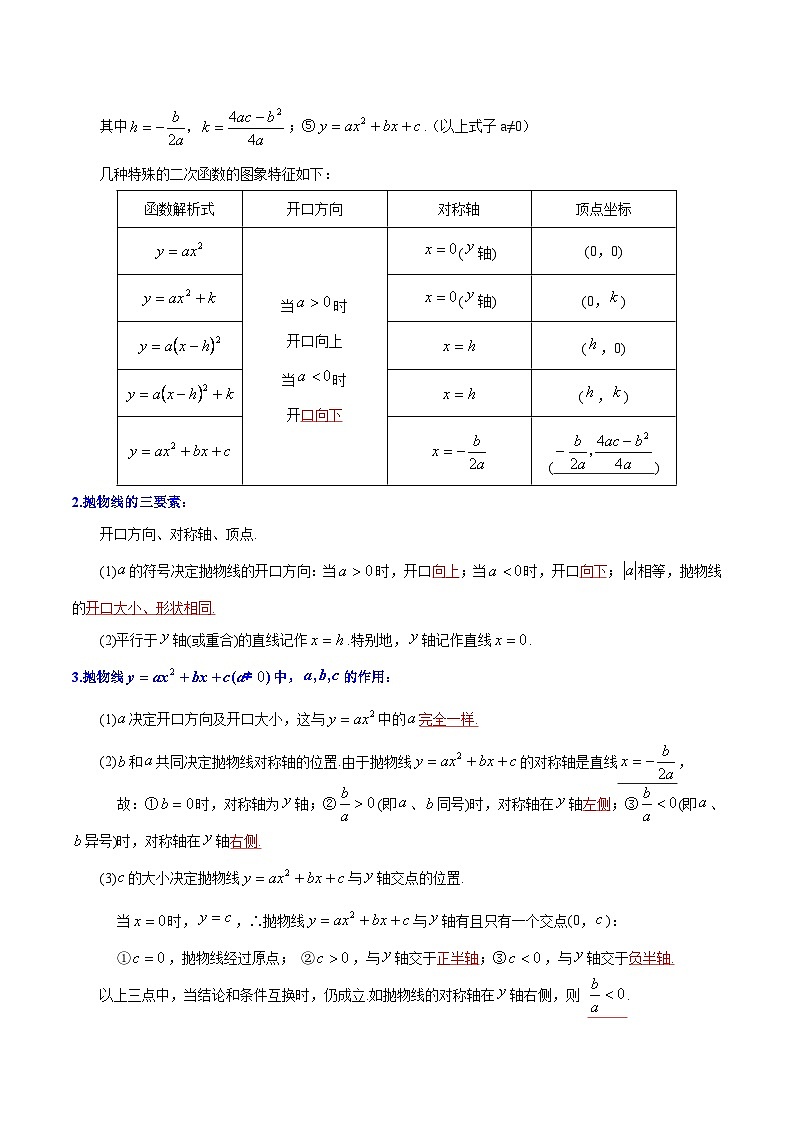
2.抛物线的三要素：
开口方向、对称轴、顶点.
(1)的符号决定抛物线的开口方向：当时，开口 ；当时，开口 ；相等，抛物线的
(2)平行于轴(或重合)的直线记作.特别地，轴记作直线.
3.抛物线 SKIPIF 1 < 0 中， SKIPIF 1 < 0 的作用：
(1)决定开口方向及开口大小，这与中的
(2)和共同决定抛物线对称轴的位置.由于抛物线的对称轴是直线 ，
故：①时，对称轴为轴；②(即、同号)时，对称轴在轴 ；③(即、异号)时，对称轴在轴 .
(3)的大小决定抛物线与轴交点的位置.
当时，，∴抛物线与轴有且只有一个交点(0，)：
①，抛物线经过原点； ②，与轴交于 ；③，与轴交于 .
以上三点中，当结论和条件互换时，仍成立.如抛物线的对称轴在轴右侧，则 .
4.用待定系数法求二次函数的解析式：
(1)一般式：（a≠0）.已知图象上三点或三对、的值，通常选择一般式.
(2)顶点式：（a≠0）.已知图象的 ，通常选择 .
(可以看成的图象平移后所对应的函数.)
(3)“交点式”：已知图象与轴的交点坐标、，通常选用 ：
（a≠0）.(由此得根与系数的关系：).
细节剖析：
求抛物线（a≠0）的对称轴和顶点坐标通常用三种方法： 这三种方法都有各自的优缺点，应根据实际灵活选择和运用．
知识点03：二次函数与一元二次方程的关系
函数，当时，得到一元二次方程，那么一元二次方程的解就是二次函数的图象与x轴交点的横坐标，因此二次函数图象与x轴的交点情况决定一元二次方程根的情况.
(1)当二次函数的图象与x轴有两个交点，这时，则方程有 ；
(2)当二次函数的图象与x轴有且只有一个交点，这时，则方程有 ；
(3)当二次函数的图象与x轴没有交点，这时，则方程 .
通过下面表格可以直观地观察到二次函数图象和一元二次方程的关系：
细节剖析：
二次函数图象与x轴的交点的个数由的值来确定.
(1)当二次函数的图象与x轴有两个交点，这时，则方程有两个 实根；
(2)当二次函数的图象与x轴有且只有一个交点，这时，则方程有两个 实根；
(3)当二次函数的图象与x轴没有交点，这时，则方程 .
知识点04：利用二次函数解决实际问题
利用二次函数解决实际问题，要建立数学模型，即把实际问题转化为二次函数问题，利用题中存在的公式、内含的规律等相等关系，建立函数关系式，再利用函数的图象及性质去研究问题.在研究实际问题时要注意自变量的取值范围应具有实际意义.
利用二次函数解决实际问题的一般步骤是：
(1)建立适当的 ；
(2)把实际问题中的一些 联系起来；
(3)用待定系数法求出 ；
(4)利用二次函数的图象及其性质去
细节剖析：
常见的问题：求最大(小)值(如 等)、 的模型问题等.解决这些实际问题关键是找等量关系，把实际问题转化为函数问题，列出相关的函数关系式.
考点提优练
考点01：二次函数图象上点的坐标特征
1．（2022秋•平阳县月考）二次函数y＝2x2的图象如图所示，点O为坐标原点，点A在y轴的正半轴上，点B、C在函数图象上，四边形OBAC为菱形，且∠AOB＝30°，则点C的坐标为（ ）
A．（﹣，）B．（﹣，）C．（﹣1，）D．（﹣1，）
2．（2022•思明区校级二模）已知抛物线y＝ax2+bx+c经过点P（2，y0），且对于抛物线上任意一点（x1，y1）都有y1≥y0，若点A（﹣2，m+2）与点B（t，n）均在该抛物线上，且m﹣n＜﹣2，则t的值可以是（ ）
A．7B．4C．1D．﹣1
3．（2022秋•通州区校级月考）设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y＝x2﹣2x+c上的三点，y1，y2，y3的大小关系为（ ）
A．y1＞y2＞y3B．y1＞y3＞y2C．y3＞y2＞y1D．y3＞y1＞y2
考点02：二次函数图象上点的坐标特征
4．（2022秋•福清市校级月考）抛物线y＝x2﹣2x﹣1与y轴的交点的坐标为 ．
5．（2022•南关区校级模拟）如图，在平面直角坐标系中，抛物线y＝ax2﹣2ax+3（a＜0）与y轴交于点A，过A作AC∥x轴交抛物线于点C，以AC为对角线作菱形ABCD，若菱形的顶点B恰好落在x轴上，则菱形ABCD的面积为 ．
6．（2022•朝阳区二模）在平面直角坐标系xOy中，已知抛物线y＝x2+（a+2）x+2a．
（1）求抛物线的对称轴（用含a的式子表示）；
（2）若点（﹣1，y1），（a，y2），（1，y3）在抛物线上，且y1＜y2＜y3，求a的取值范围．
7．（2018•黄冈）已知直线l：y＝kx+1与抛物线y＝x2﹣4x．
（1）求证：直线l与该抛物线总有两个交点；
（2）设直线l与该抛物线两交点为A，B，O为原点，当k＝﹣2时，求△OAB的面积．
考点03：二次函数图象与几何变换
8．（2022•宿豫区开学）将抛物线y＝（x﹣3）2﹣4先向右平移1个单位长度，再向上平移2个单位长度，得到的抛物线的函数表达式为（ ）
A．y＝（x﹣4）2﹣6B．y＝（x﹣1）2﹣3C．y＝（x﹣2）2﹣2D．y＝（x﹣4）2﹣2
9．（2022•瑞安市校级三模）如图，将一个含45°的直角三角板ABC放在平面直角坐标系的第一象限，使直角顶点A的坐标为（1，0），点C在y轴上．过点A，C作抛物线y＝2x2+bx+c，且点A为抛物线的顶点．要使这条抛物线经过点B，那么抛物线要沿对称轴向下平移（ ）
A．5个单位B．6个单位C．7个单位D．8个单位
10．（2022•揭阳一模）抛物线y＝（x﹣1）2+3关于x轴对称的抛物线的解析式是 ．
11．（2022•浦江县模拟）如图，抛物线y＝﹣x2+1与抛物线y＝kx2﹣2的交点在x轴上，现将抛物线y＝﹣x2+1向下平移个单位，y＝kx2﹣2向上平移 个单位，平移后两条抛物线的交点还在x轴上．
12．（2021秋•蜀山区期末）在平面直角坐标系xOy中，已知点A（﹣1，1）在抛物线y＝x2+2bx+c上．
（1）c＝ （用含b的式子表示）；
（2）若将该抛物线向右平移t个单位（t≥），平移后的抛物线仍经过A（﹣1，1），则平移后抛物线的顶点纵坐标的最大值为 ．
13．（2022•河北）如图，点P（a，3）在抛物线C：y＝4﹣（6﹣x）2上，且在C的对称轴右侧．
（1）写出C的对称轴和y的最大值，并求a的值；
（2）坐标平面上放置一透明胶片，并在胶片上描画出点P及C的一段，分别记为P′，C′．平移该胶片，使C′所在抛物线对应的函数恰为y＝﹣x2+6x﹣9．求点P′移动的最短路程．
14．（2021•陕西模拟）如图，抛物线y＝ax2+bx+c经过A（1，0），B（3，0），C（0，6）三点．
（1）求抛物线的表达式；
（2）抛物线的顶点M与对称轴l上的点N关于x轴对称，直线AN交抛物线于点D．直线BE交AD于点E，若直线BE将△ABD的面积分为1：2的两部分，求点E的坐标．
考点04：二次函数的三种形式
15．（2022•成都模拟）将二次函数y＝x2﹣14x+13化为y＝（x﹣h）2+k的形式，结果为（ ）
A．y＝（x+7）2+49B．y＝（x+7）2﹣36
C．y＝（x﹣7）2+49D．y＝（x﹣7）2﹣36
16．（2021秋•三明期末）将二次函数y＝x2﹣4x+3通过配方可化为y＝a（x﹣h）2+k的形式，结果为（ ）
A．y＝（x﹣2）2﹣1B．y＝（x﹣2）2+3C．y＝（x+2）2+3D．y＝（x+2）2﹣1
17．（2020秋•龙岩期末）将二次函数y＝x2+6x+2化成y＝（x﹣h）2+k的形式应为（ ）
A．y＝（x+3）2﹣7B．y＝（x﹣3）2+11
C．y＝（x+3）2﹣11D．y＝（x+2）2+4
18．（2019秋•大连期中）将二次函数y＝﹣x2+4x﹣5化为y＝a（x﹣h）2+k的形式为（ ）
A．y＝﹣（x+2）2﹣1B．y＝﹣（x+2）2+1
C．y＝﹣（x﹣2）2+1D．y＝﹣（x﹣2）2﹣1
19．（2020秋•合肥期末）已知二次函数y＝﹣2x2﹣4x+1，先用配方法转化成y＝a（x﹣h）2+k，再写出函数的顶点坐标、对称轴以及描述该函数的增减性．
20．（2017秋•绥滨县校级月考）用配方法把二次函数y＝x2﹣4x+5化为y＝a（x﹣h）2+k的形式，再指出该函数图象的开口方向、对称轴和顶点坐标．
考点05：抛物线与x轴的交点
21．（2022秋•温州月考）如图，抛物线y＝﹣x2+2x+1交x轴于A，B两点，交y轴于点C，点D为抛物线的顶点，点C关于抛物线的对称轴的对称点为点E，点G，F分别在x轴和y轴上，则四边形EDFG周长的最小值为（ ）
A．6B．4C．D．2
22．（2022•内蒙古）如图，抛物线y＝ax2+bx+c（a≠0）与x轴的一个交点坐标为（﹣1，0），抛物线的对称轴为直线x＝1，下列结论：①abc＜0②3a+c＝0③当y＞0时，x的取值范围是﹣1≤x＜3④点（﹣2，y1），（2，y2）都在抛物线上，则有y1＜0＜y2.其中结论正确的个数是（ ）
A．1个B．2个C．3个D．4个
23．（2022秋•鄞州区校级月考）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，比较下列各式与0的大小．
①abc 0；
②b2﹣4ac 0；
③（a+c）2﹣b2 0．
24．（2022•南关区校级模拟）如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA＝OB，顶点C、D在第一象限，经过点A、C、D三点的抛物线y＝﹣x2+bx+c交x轴正半轴于点E，则点E的坐标为 ．
25．（2022春•长沙期末）定义：如果抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（x1，0），B（x2，0），那么我们把线段AB叫做雅礼弦，AB两点之间的距离l称为抛物线的雅礼弦长．
（1）求抛物线y＝x2﹣2x﹣3的雅礼弦长；
（2）求抛物线y＝x2+（n+1）x﹣1（1≤n＜3）的雅礼弦长的取值范围；
（3）设m，n为正整数，且m≠1，抛物线y＝x2+（4﹣mt）x﹣4mt的雅礼弦长为l1，抛物线y＝﹣x2+（t﹣n）x+nt的雅礼弦长为l2，s＝l12﹣l22，试求出s与t之间的函数关系式，若不论t为何值，s≥0恒成立，求m，n的值．
26．（2022•东明县二模）已知抛物线y＝﹣x2+bx+c与x轴交于点A和点B（3，0），与y轴交于点C（0，3），P是线段BC上一点，过点P作PN∥y轴交x轴于点N，交抛物线于点M．
（1）求该抛物线的表达式；
（2）如果点P的横坐标为2，点Q是第一象限抛物线上的一点，且△QMC和
△PMC的面积相等，求点Q的坐标．
考点06：二次函数的应用
27．（2022秋•通州区校级月考）使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）近似满足函数关系式y＝ax2+bx+c（a≠0），如图记录了某种家用节能燃气灶烧开同一壶水的旋钮的旋转角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋较角度约为（ ）度．
A．36B．45C．50D．42
28．（2022•杏花岭区校级模拟）太原某中学利用学校的体育场地设施和设备，充分调动全体师生的积极性，广泛开展各项体育活动，努力提高学生的身体素质，如图①是小杰在铅球比赛中的一次掷球，铅球出手以后的轨迹可近似看作是抛物线的一部分，已知铅球出手时离地面1.6米，铅球离抛掷点水平距离3米时达到最高，此时铅球离地面2.5米，如图②，以水平面为x轴，小杰所站位置的铅垂线为y轴建立平面直角坐标系，则他掷铅球的运动路线的函数表达式为（ ）
A．B．
C．D．
29．（2022•石家庄三模）某池塘的截面如图所示，池底呈抛物线形，在图中建立平面直角坐标系，并标出相关数据（单位：m）．有下列结论：
①AB＝24m；
②池底所在抛物线的解析式为y＝﹣5；
③池塘最深处到水面CD的距离为1.8m；
④若池塘中水面的宽度减少为原来的一半，
则最深处到水面的距离减少为原来的．
其中结论正确的是（ ）
A．①②B．②④C．③④D．①④
30．（2022•沂南县一模）足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如表：下列结论不正确的是（ ）
A．足球距离地面的最大高度超过20m
B．足球飞行路线的对称轴是直线t＝
C．点（10，0）在该抛物线上
D．足球被踢出5s～7s时，距离地面的高度逐渐下降
31．（2022•徐州一模）北京冬奥会跳台滑雪项目比赛其标准台高度是90m．运动员起跳后的飞行路线可以看作是抛物线的一部分，运动员起跳后的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某运动员起跳后的x与y的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为（ ）
A．10mB．15mC．20mD．22.5m
32．（2022•新乐市校级模拟）某超市销售一款洗手液，其成本价为每瓶16元，当销售单价定为20元时，每天可售出80瓶．根据市场行情，现决定降价销售．市场调查反映：销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），若设这款的销售单价为x（元），每天的销售量为（瓶）．
（1）每天的销售量y（瓶）与销售单价x（元）之间的函数关系式为 ；
（2）销售这款“洗手液”每天的最大利润为 ．
33．（2022•新乐市校级模拟）某市政府加大各部门和单位对口扶贫力度．某单位的帮扶对象种植的农产品在某月（按30天计）的第x天（x为正整数）的销售价格p（元/千克）关于x的函数关系式为p＝销售量y（千克）与x之间的关系如图所示．
（1）求y与x之间的函数关系式为y＝ ；
（2）若该农产品当月的销售额最大，最大销售额是 .（销售额＝销售量×销售价格）
34．（2022•威县校级模拟）弹力球游戏规则：弹力球抛出后与地面接触一次，弹起降落，若落入筐中，则游戏成功．弹力球着地前后的运动轨迹可近似看成形状相同的两条抛物线．如图16，甲站在原点处，从离地面高度为1m的点A处抛出弹力球，弹力球在B处着地后弹起，落至点C处，弹力球第一次着地前抛物线的解析式为y＝a（x﹣2）2+2．
（1）a的值为 ；点B的横坐标为 ；
（2）若弹力球在B处着地后弹起的最大高度为着地前手抛出的最大高度的一半．
①求弹力球第一次着地后抛物线解析式；
②求弹力球第二次着地点到点O的距离；
③如果摆放一个底面半径为0.5m，高0.5m的圆柱形筐，且筐的最左端距离原点9m，若要甲能投球成功，需将筐沿x轴向左移动bm，直接写出b的取值范围．
35．（2022•江汉区校级模拟）某公司分别在A、B两城生产同种产品共100件．A城生产产品的总成本y（万元）与产品数量x（件）之间满足函数关系y＝2x2+100x．B城生产产品每件的成本s（万元）与产品数量t（件）满足函数关系s＝t+20．
（1）设A城生产产品的数量有x件，直接用含x的代数式表示下列各量：
①B城生产产品的数量为 件； ②B城生产产品的总成本为 万元；
（2）当A、B两城生产这批产品的总成本的和最少时，求A，B两城各生产多少件？
（3）现把A，B城所生产产品运往C，D两地．从A城运往C、D两地的费用分别是m万元/件和3万元/件；从B城运往C、D两地的费用分别是1万元/件和2万元/件，C地需要90件，D地需要10件，在（2）的条件下，A、B两城的总运费的最小值为120万元，直接写出m的值为 ．
36．（2022•海曙区校级模拟）某城市发生疫情，第x天（1≤x≤15）新增病例y（人）如下表所示：
（1）疫情前15天的人数模型基本符合二次函数y＝ax2+bx+c．根据图表，求出二次函数解析式．
（3）由于疫情传染性强，第15天开始新增病例人数模型发生变化，第x天（x≥15）新增病例y（人）近似满足y＝﹣5（x﹣m）（x﹣13）．请预计第几天新增病例清零．
（3）为应对本轮疫情，按照每一确诊病例需当天提供一张病床的要求，政府应该在哪一天提供的病床最多？最多应该提供多少张？函数解析式
开口方向
对称轴
顶点坐标
当时
开口向上
当时
开
(轴)
(0，0)
(轴)
(0，)
(，0)
(，)
( )
的图象
的解
方程有两个 实数解
方程有 实数解
方程 实数解
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
x
1
2
3
4
…
11
…
y
2
11
22
35
…
182
…