人教版数学九年级上册期末章节重难点复习讲义第24章 圆（2份，原卷版+解析版）

这是一份人教版数学九年级上册期末章节重难点复习讲义第24章 圆（2份，原卷版+解析版），文件包含人教版数学九年级上册期末章节重难点复习讲义第24章圆原卷版doc、人教版数学九年级上册期末章节重难点复习讲义第24章圆解析版doc等2份试卷配套教学资源，其中试卷共80页， 欢迎下载使用。

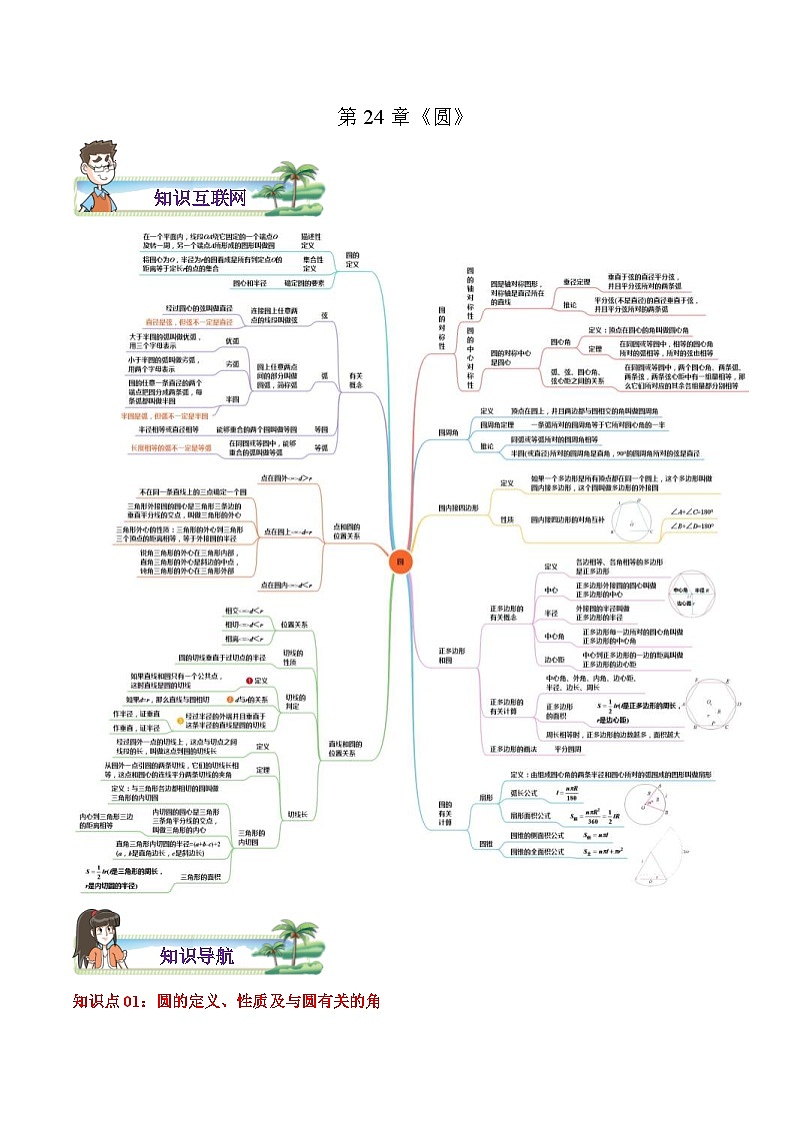
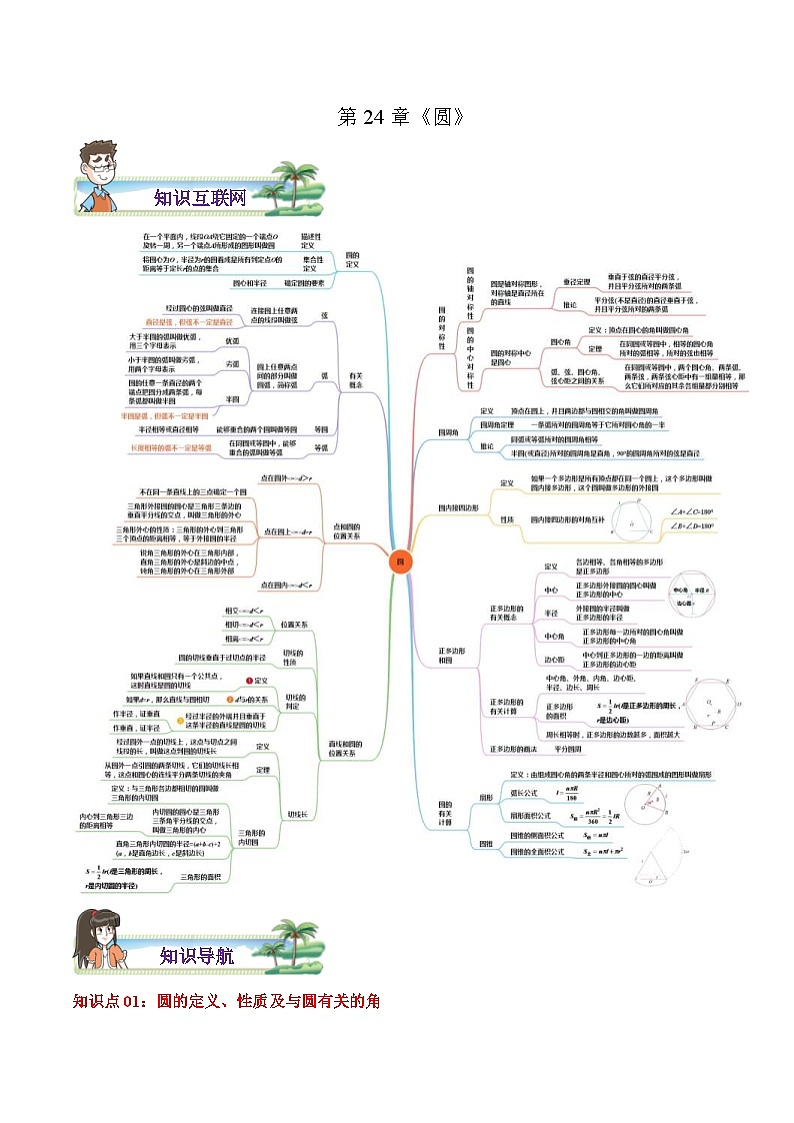
知识导航
知识点01：圆的定义、性质及与圆有关的角
1．圆的定义
(1)线段OA绕着它的一个端点O ，另一个端点A所形成的 ，叫做圆.
(2)圆是到
细节剖析：
①圆心确定圆的 ，半径确定圆的 ；确定一个圆应先确定 ，再确定 ，二者缺一不可；
②圆是一条 .
2．圆的性质
(1)旋转 ：圆是 ，绕圆心旋转任一角度都和原来图形 ；圆是 图形，对称中心是
在 中，两个圆心角，两条弧，两条弦，两条弦心距，这四组量中的任意一
组 ，那么它所对应的其他各组分别相等.
(2)轴对称：圆是 ， 都是它的对称轴.
(3)垂径定理及推论：
①垂直于弦的直径 这条弦，并且平分弦所对的 .
②平分弦(不是直径)的直径 于弦，并且平分弦所对的 .
③弦的垂直平分线过 ，且平分弦对的两条弧.
④平分一条弦所对的两条弧的直线过圆心，且 此弦.
⑤ 相等.
细节剖析：
在垂经定理及其推论中： 所对的优弧、平分弦所对的劣弧，在这五个条件中，知道任意两个，就能推出其他三个结论.（注意：“ ”作为题设时，平分的弦不能是直径）
3．两圆的性质
(1)两个圆是一个 形，对称轴是
(2)相交两圆的连心线 公共弦，相切两圆的连心线经过
4．与圆有关的角
(1)圆心角： 叫圆心角.
圆心角的性质： 等于它所对的弧的度数.
(2)圆周角：顶点在 叫做圆周角.
圆周角的性质：
①圆周角等于它
② 所对的圆周角相等；在 中，相等的圆周角所对的弧相等.
③90°的圆周角所对的弦为 ；半圆或直径所对的圆周角为 .
④如果三角形 ，那么这个三角形是直角三角形.
⑤圆内接四边形的 互补；外角等于它的
细节剖析：
(1)圆周角必须满足两个条件：①顶点在 ；②角的两边都和圆 (2)圆周角定理成立的前提条件是在 中.
知识点02：与圆有关的位置关系
1．判定一个点P是否在⊙O上
设⊙O的半径为，OP=，则有
点P在⊙O 外； 点P在⊙O 上；点P在⊙O 内.
细节剖析：
点和圆的 和点到圆心的距离的 是相对应的，即知道位置关系就可以确定 ；知道数量关系也可以确定 .
2．判定几个点 SKIPIF 1 < 0 在同一个圆上的方法
当时，在⊙O 上.
3．直线和圆的位置关系
设⊙O 半径为R，点O到直线的距离为.
(1)直线和⊙O没有公共点直线和圆相离.
(2)直线和⊙O有唯一公共点直线和⊙O相切.
(3)直线和⊙O有两个公共点直线和⊙O相交.
4．切线的判定、性质
(1)切线的判定：
① 是圆的切线.
② 是圆的切线.
(2)切线的性质：
①圆的切线 于过切点的半径.
②经过圆心作圆的切线的 经过切点.
③经过 作切线的垂线经过 .
(3)切线长：从圆外一点作圆的切线，这 叫做切线长.
(4)切线长定理：从圆外一点作 ，它们的切线长相等， 平分两条切线的夹角.
5．圆和圆的位置关系
设的半径为，圆心距.
(1)和没有公共点，且每一个圆上的所有点在另一个圆的外部外离
.
(2)和没有公共点，且的每一个点都在内部内含
(3)和有唯一公共点，除这个点外，每个圆上的点都在另一个圆外部外切.
(4)和有唯一公共点，除这个点外，的每个点都在内部内切.
(5)和有两个公共点相交.
知识点03：三角形的外接圆与内切圆、圆内接四边形与外切四边形
1．三角形的内心、外心、重心、垂心
(1)三角形的内心：是 ，它是三角形内切圆的圆心，在三角形内部，它到三角形三边的距离相等，通常用“I”表示.
(2)三角形的外心：是 ，它是三角形外接圆的圆心，锐角三角形外心在三角形内部，直角三角形的外心是斜边中点，钝角三角形外心在三角形外部，三角形外心到三角形三个顶点的距离相等，通常用O表示.
(3)三角形重心：是 ，在三角形内部；它到顶点的距离是到对边中点距离的2倍，通常用G表示.
(4)垂心：是
细节剖析：
(1) 任何一个三角形都 内切圆，但任意一个圆都有 外切三角形；
(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于 ，即 (S为三角形的面积，P为三角形的周长，r为内切圆的半径).
(3) 三角形的外心与内心的区别：
2．圆内接四边形和外切四边形
(1) 叫圆的内接四边形，圆内接四边形对角 ，外角等于 (2) 叫圆外切四边形，圆 相等.
知识点04：圆中有关计算
1．圆中有关计算
圆的面积公式： ，周长 .
圆心角为、半径为R的弧长 .
圆心角为，半径为R，弧长为的扇形的面积 .
弓形的面积要转化为扇形和三角形的面积和、差来计算.
圆柱的侧面图是一个矩形，底面半径为R，母线长为的圆柱的体积为，侧面积为，全面积为 .
圆锥的侧面展开图为扇形，底面半径为R，母线长为，高为的圆锥的侧面积为，全面积为，母线长、圆锥高、底面圆的半径之间有 .
细节剖析：
(1)对于扇形面积公式，关键要理解圆心角是1°的扇形面积是圆面积的，
即 ；
(2)在扇形面积公式中，涉及三个量：扇形面积S、扇形半径R、扇形的圆心角，知道其中的两个量就可以求出第三个量.
(3)扇形面积公式 ，可根据题目条件灵活选择使用，它与三角形面积公式有点类似，可类比记忆；
(4)扇形两个面积公式之间的联系： .
考点提优练
考点01：垂径定理
1．（2022•荆门）如图，CD是圆O的弦，直径AB⊥CD，垂足为E，若AB＝12，BE＝3，则四边形ACBD的面积为（ ）
A．36B．24C．18D．72
2．（2022秋•南岗区校级月考）如图，在⊙O中，AD⊥BC，连接AB、CD，当AB＝2，CD＝6时，则⊙O半径长为 ．
3．（2022•烟台模拟）如图，AB是⊙O的直径，弦CD交AB于点P，AP＝4，BP＝12，∠APC＝30°，则CD的长为 ．
4．（2022•开福区一模）如图，在⊙O中，AB、AC是互相垂直且相等的两条弦，OD⊥AB，OE⊥AC，垂足分别为D、E．
（1）求证：四边形ADOE是正方形；
（2）若AC＝2cm，求⊙O的半径．
5．（2021秋•嘉祥县期末）如图，线段AB＝10，AC＝8，点D，E在以AB为直径的半圆O上，且四边形ACDE是平行四边形，过点O作OF⊥DE于点F，求AE的长．
6．（2021•浦东新区模拟）如图，已知AB是圆O的直径，弦CD交AB于点E，∠CEA＝30°，OE＝4，DE＝5，求弦CD及圆O的半径长．
7．（2022•宣州区二模）如图所示的是一圆弧形拱门，其中路面AB＝2m，拱高CD＝3m，则该拱门的半径为（ ）
A．B．2mC．D．3m
考点02：圆周角定理
8．（2022•梁子湖区二模）如图，点A，B，C，D在⊙O上，AO⊥BC于点E，若∠BDC＝150°，AE长为2+，则弦BC的长为（ ）
A．2B．C．2D．4
9．（2022•南京模拟）如图，在⊙O中，CD是⊙O上的一条弦，直径AB⊥CD，连接AC、OD，∠A＝26°，则∠D的度数是（ ）
A．26°B．38°C．52°D．64°
10．（2022•姑苏区校级一模）如图，线段CD上一点O，以O为圆心，OD为半径作圆，⊙O上一点A，连结AC交⊙O于B点，连结BD，若BC＝BD，且∠C＝25°，则∠BDA＝ ．
11．（2022•宜兴市校级二模）如图，平面直角坐标系中，点A的坐标为（2，1），点C（x，y）为平面内一动点，以AC为直径作⊙E，若过点且平行于x轴的直线被⊙E所截的弦GH长为．则y与x之间的函数关系式是 ；经过点A的直线y＝k（x﹣2）+1（k＜0）与点C运动形成的图象交于B，D两点（点D在点B的右侧），F为该图象的最高点，若△ADF的面积是△ABF面积的3倍，则k＝ ．
12．（2022春•鼓楼区校级月考）如图，AB为半圆O的直径，CD＝AB＝2，AD，BC交于点E，且E为CB的中点，F为弧AC的中点，连接EF，求EF的长．
13．（2022•西安模拟）如图，四边形ABCD内接于⊙O，∠ADC＝90°．连接BD，作CF⊥BD，分别交BD，⊙O于点E，F，连接BF，交AD于点M，AB＝BC．
（1）求证：BF∥CD．
（2）当AD+CD＝5时，求线段BD的长．
考点03：切线的判定与性质
14．（2022•社旗县一模）如图，直线交x轴于点A，交y轴于点B，点P是x轴上一动点，以点P为圆心，以1个单位长度为半径作⊙P，当⊙P与直线AB相切时，点P的坐标是（ ）
A．B．或
C．D．或
15．（2022•新河县二模）如图，在直线l上有相距7cm的两点A和O（点A在点O的右侧），以O为圆心作半径为1cm的圆，过点A作直线AB⊥l．将⊙O以2cm/s的速度向右移动（点O始终在直线l上），则⊙O与直线AB在（ ）秒时相切．
A．3B．3.5C．3或4D．3或3.5
16．（2021秋•海州区期中）如图，在矩形ABCD中，AB＝6，BC＝4，以CD为直径作⊙O．将矩形ABCD绕点C旋转，使所得矩形A'B'CD'的边A'B'与⊙O相切，切点为E，边CD'与⊙O相交于点F，则CF的长为（ ）
A．6﹣B．4C．5D．3
17．（2022•晋江市模拟）如图，在平面直角坐标系中，点A（2，0），点B是直线y＝﹣x上的一个动点，以A为圆心，以线段AB的长为半径作⊙A，当⊙A与直线y＝﹣x相切时，点B的坐标为 ．
18．（2022•宜兴市一模）如图，在四边形ABCD中，AD＝CD＝2，CB＝AB＝6，∠BAD＝∠BCD＝90°，点E在对角线BD上运动，⊙O为△DCE的外接圆，当⊙O与AD相切时，⊙O的半径为 ；当⊙O与四边形ABCD的其它边相切时，其半径为 ．
19．（2021秋•南皮县校级月考）如图，正方形ABCD的边长为8，M是AB的中点，P是边BC上的动点，连接PM，以点P为圆心，PM长为半径作⊙P．
（1）当BP＝3时，点C在⊙P ；（填“上“内“或“外“）
（2）当⊙P与正方形ABCD的边相切时，BP的长为 ．
20．（2022•五华区校级模拟）如图，AB为⊙O直径，C，D为⊙O上的两点，且∠ACD＝2∠A，CE⊥DB交DB的延长线于点E．
（1）求证：CE是⊙O的切线；
（2）若DE＝2CE，AC＝4，求⊙O的半径．
21．（2022•金水区校级模拟）如图，AE是半圆O的直径，D是半圆O上不同于A，E的一点，作∠FAD＝∠DAE，过点D作DC⊥AF于点C，CD的延长线与AE的延长线相交于点B．
（1）求证：CD是半圆O所在圆的切线；
（2）若，AC＝4，求⊙O的半径．
22．（2022•河南模拟）如图所示，在Rt△ABC中，∠BAC＝90°，以AB为直径作⊙O交BC于点D，E是AC的中点，连接ED．点F在上．且FO⊥AB，连接BF并延长交AC的延长线于点C．
（1）求证：DE是⊙O的切线；
（2）连接AF，试说明AF、BG的数量关系．
考点04：切线长定理
23．（2021秋•西岗区期末）如图，P为⊙O外一点，PA、PB分别切⊙O于点A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA＝8，则△PCD的周长为（ ）
A．8B．12C．16D．20
24．（2020•河北模拟）如图，⊙O内切于正方形ABCD，O为圆心，作∠MON＝90°，其两边分别交BC，CD于点N，M，若CM+CN＝4，则⊙O的面积为（ ）
A．πB．2πC．4πD．0.5π
25．（2022•拱墅区模拟）如图，AB、AC、BD是⊙O的切线，切点分别是P、C、D．若AB＝10，AC＝6，则BD的长是（ ）
A．3B．4C．5D．6
26．（2021秋•高阳县期末）如图，△ABC是一张周长为17cm的三角形的纸片，BC＝5cm，⊙O是它的内切圆，小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，则剪下的三角形的周长为（ ）
A．12cmB．7cm
C．6cmD．随直线MN的变化而变化
27．（2021秋•兴化市月考）如图，以正方形ABCD的AB边为直径作半圆O，过点C作直线切半圆于点F，交AD边于点E，若△CDE的周长为12，则直角梯形ABCE周长为 ．
28．（2015秋•宜兴市校级期中）如图，△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，
已知AD＝10cm，小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形（△AMN），则剪下的△AMN的周长为 ．
29．（2013•西藏模拟）如图，AD、AE、CB都是⊙O的切线，切点分别为D、E、F，AD＝4cm，则△ABC的周长是 ．
30．（2021秋•原州区期末）如图，PA、PB、DE分别切⊙O于A、B、C，DE分别交PA，PB于D、E，已知P到⊙O的切线长为8cm，那么△PDE的周长为 ．
31．（2011秋•海淀区期中）如图，AB为⊙O的直径，点C在AB的延长线上，CD、CE分别与⊙O相切于点D、E，若AD＝2，∠DAC＝∠DCA，则CE＝ ．
32．（2021•滨海县一模）如图，PA、PB是⊙O的切线，CD切⊙O于点E，△PCD的周长为12，∠APB＝60°．求：
（1）PA的长；
（2）∠COD的度数．
33．（2018秋•硚口区期末）如图，AB为⊙O直径，PA、PC分别与⊙O相切于点A、C，PQ⊥PA，PQ交OC的延长线于点Q．
（1）求证：OQ＝PQ；
（2）连BC并延长交PQ于点D，PA＝AB，且CQ＝6，求BD的长．
34．（2012秋•姜堰市校级月考）如图，PA、PB是⊙O的切线，切点分别是A、B，直线EF也是⊙O的切线，切点为Q，交PA、PB于点E、F，已知PA＝12cm，∠P＝40°
①求△PEF的周长；
②求∠EOF的度数．
35．（2008秋•恩平市校级期中）如图，P是⊙O外的一点，PA、PB分别与⊙O相切于点A、B，C是上的任意一点，过点C的切线分别交PA、PB于点D、E．
（1）若PA＝4，求△PED的周长；
（2）若∠P＝40°，求∠AFB的度数．
考点05：正多边形和圆
36．（2022春•新昌县期末）如图，在同一平面内，将边长相等的正六边形、正方形的一边重合，则∠1的度数为（ ）
A．18°B．25°C．30°D．45°
37．（2022•石家庄三模）如图，边长相等的正八边形和正方形部分重叠摆放在一起，已知正方形面积是2，那么非阴影部分面积是（ ）
A．6B．C．D．8
38．（2022•沙湾区模拟）已知图标（如图）是由圆的六个等分点连接而成，若圆的半径为1，则阴影部分的面积等于 ．
39．（2022•雁塔区校级模拟）在正六边形ABCDEF中，对角线AC，BD相交于点M，则的值为 ．
40．（2022•咸安区模拟）如图，边长为2的正六边形ABCDEF的中心与坐标原点O重合，AF∥y轴，将正六边形ABCDEF绕原点O逆时针旋转n次，每次旋转60°，当n＝2024时，顶点A的坐标为 ．
41．（2022春•思明区校级期中）如图，等边三角形ABC内接于半径长为2的⊙O，点P在圆弧AB上以2倍速度从B向A运动，点Q在圆弧BC上以1倍速度从C向B运动，当点P，O，Q三点处于同一条直线时，停止运动．
（1）求点Q的运动总长度；
（2）若M为弦PB的中点，求运动过程中CM的最大值．
42．（2021秋•日喀则市月考）如图，正方形ABCD是半径为R的⊙O内接四边形，R＝6．
求正方形ABCD的边长和边心距．
43．（2019秋•垦利区期中）七年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果，内容如下：
（1）如图1，等边三角形ABC中，在AB、AC边上分别取点M、N，使BM＝AN，连接BN、CM，发现BN＝CM，且∠NOC＝60°，试说明：∠NOC＝60°．
（2）如图2，正方形ABCD中，在AB、BC边上分别取点M、N，使AM＝BN，连接AN、DM，那么∠DON＝ 度，并说明理由．
（3）如图3，正五边形ABCDE中，在AB、BC边上分别取点M、N，使AM＝BN，连接AN、EM，那么AN＝ ，且∠EON＝ 度．（正n边形内角和（n﹣2）×180°，正多边形各内角相等）
考点06：扇形面积的计算
44．（2022•山西模拟）如图，在△ABC中，AB＝AC＝4，∠BAC＝120°，AO是△ABC的中线．以O为圆心，OA长为半径作半圆，分别交AB，AC于点D，E，交BC于点F，G．则图中阴影部分的面积为（ ）
A．2﹣πB．C．4﹣πD．π
45．（2022春•大同期末）如图，正方形ABCD的边长为4，先以正方形的对角线AC为直径画圆，再以正方形的各边长为直径画半圆，则图中阴影部分的面积为（ ）
A．16B．8πC．16πD．8
46．（2022•巴南区自主招生）如图，正方形ABCD的边长为6，四条弧分别以相应顶点为圆心、正方形ABCD边长为半径，则图中阴影部分的面积为 （结果保留π）．
47．（2022•渝中区校级开学）如图，以菱形ABCD的顶点A为圆心，AB的长为半径作圆，点C恰好在⊙A在上，点E是AB的中点，连接CE．若AD＝6，则图中阴影部分的面积为 （结果保留π）．
48．（2022•临沭县二模）如图，在⊙O中，AC为⊙O的直径，AB为⊙O的弦，点E是的中点，过点E作AB的垂线，交AB于点M，交⊙O于点N，分别连接EB，CN．
（1）EM与BE的数量关系是 ；
（2）求证：＝；
（3）若AM＝，MB＝2，求阴影部分图形的面积．
49．（2021秋•亭湖区期末）《九章算术》是我国古代数学成就的杰出代表．其中《方田》章给出计算弧田面积的公式为：弧田面积＝（弦×矢+矢2）．如图，弧田由圆弧和其所对弦所围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差．按照上述公式计算所得弧田面积与其实际面积之间存在误差．现有圆心角∠AOB为120°，弦长AB＝2m的弧田．
（1）计算弧田的实际面积；
（2）按照《九章算术》中弧田面积的公式计算所得结果与（1）中计算的弧田实际面积相差多少平方米？（取π近似值为3，近似值为1.7）
名称
确定方法
图形
性质
外心(三角形外接圆的圆心)
三角形三边中垂线的交点
(1)OA=OB=OC；(2)外心不一定在三角形内部
内心(三角形内切圆的圆心)
三角形三条角平分线的交点
(1)到三角形三边距离相等；(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB； (3)内心在三角形内部.