苏科版（2024）七年级上册（2024）5.2 运动 想象优秀综合训练题

这是一份苏科版（2024）七年级上册（2024）5.2 运动 想象优秀综合训练题，文件包含52运动想象4大题型提分练原卷版docx、52运动想象4大题型提分练解析版docx等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。

题型一 点、线、面、体
1．几何图形都是由点、线、面、体组成的，点动成线，线动成面，面动成体，下列生活现象中可以反映“点动成线”的是
A．流星划过夜空B．打开折扇
C．汽车雨刷的转动D．旋转门的旋转
【详解】解：、流星划过夜空，属于点动成线，本选项符合题意；
、打开折扇，属于线动成面，本选项不合题意；
、汽车雨刷的转动，属于线动成面，本选项不合题意；
、旋转门的旋转，属于面动成体，本选项不合题意．
故本题选：．
2．下面现象说明“线动成面”的是
A．旋转一扇门，门在空中运动的痕迹
B．扔一块小石子，石子在空中飞行的路线
C．天空划过一道流星
D．汽车雨刷在挡风玻璃上面画出的痕迹
【详解】解：、旋转一扇门，门在空中运动的痕迹是“面动成体”，故本选项错误；
、扔一块小石子，石子在空中飞行的路线是“点动成线”，故本选项错误；
、天空划过一道流星是“点动成线”，故本选项错误；
、汽车雨刷在挡风玻璃上面画出的痕迹是“线动成面”，故本选项正确．
故本题选：．
3．你见过一种折叠灯笼吗？它看起来是平面的，可是提起来后却变成了美丽的灯笼，这个过程可近似地用哪个数学原理来解释
A．点动成线B．线动成面
C．面动成体D．面与面相交的地方是线
【详解】解：由平面图形变成立体图形的过程是面动成体．
故本题选：．
4．在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝，密密麻麻地斜织着”的语句，这里把雨看成了线，这种生活现象可以反映的数学原理是 ．
【详解】解：∵“雨”可以简单的看作“点”，“牛毛、花针、细丝”可以简单的看作“线”，
∴这种生活现象可以反映的数学原理是点动成线．
故本题答案为：点动成线．
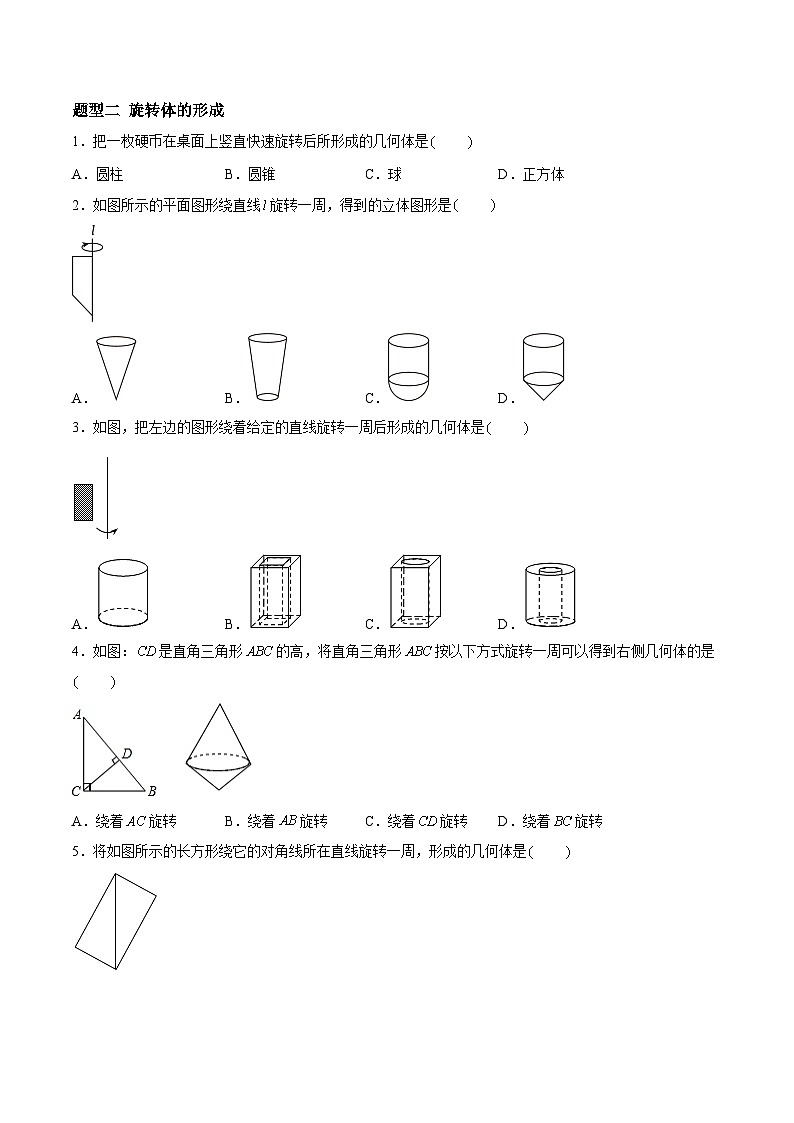
题型二 旋转体的形成
1．把一枚硬币在桌面上竖直快速旋转后所形成的几何体是
A．圆柱B．圆锥C．球D．正方体
【详解】解：把一枚硬币在桌面上竖直快速旋转后所形成的几何体是球．
故本题选：．
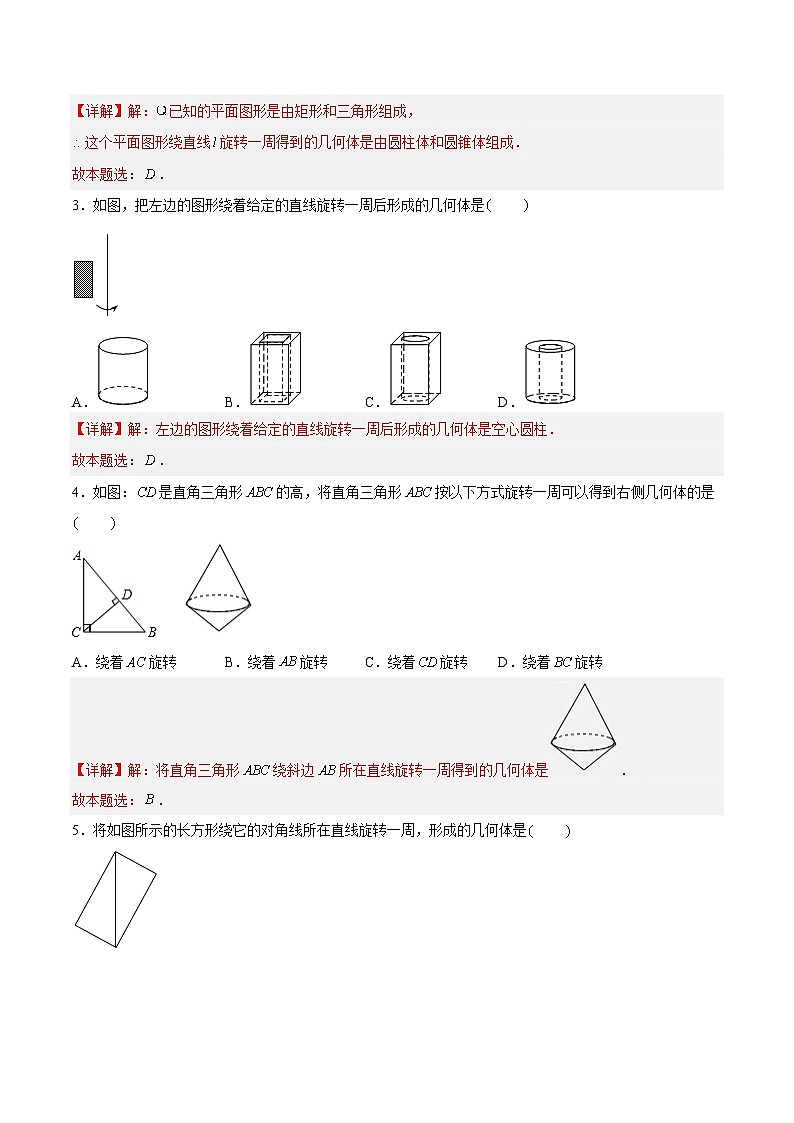
2．如图所示的平面图形绕直线旋转一周，得到的立体图形是
A．B．C．D．
【详解】解：已知的平面图形是由矩形和三角形组成，
这个平面图形绕直线旋转一周得到的几何体是由圆柱体和圆锥体组成．
故本题选：．
3．如图，把左边的图形绕着给定的直线旋转一周后形成的几何体是
A．B．C．D．
【详解】解：左边的图形绕着给定的直线旋转一周后形成的几何体是空心圆柱．
故本题选：．
4．如图：是直角三角形的高，将直角三角形按以下方式旋转一周可以得到右侧几何体的是

A．绕着旋转B．绕着旋转C．绕着旋转D．绕着旋转
【详解】解：将直角三角形绕斜边所在直线旋转一周得到的几何体是．
故本题选：．
5．将如图所示的长方形绕它的对角线所在直线旋转一周，形成的几何体是
A．B．C．D．
【详解】解：一个长方形绕它的对角线所在直线旋转一周，形成的几何体是．
故本题选：．
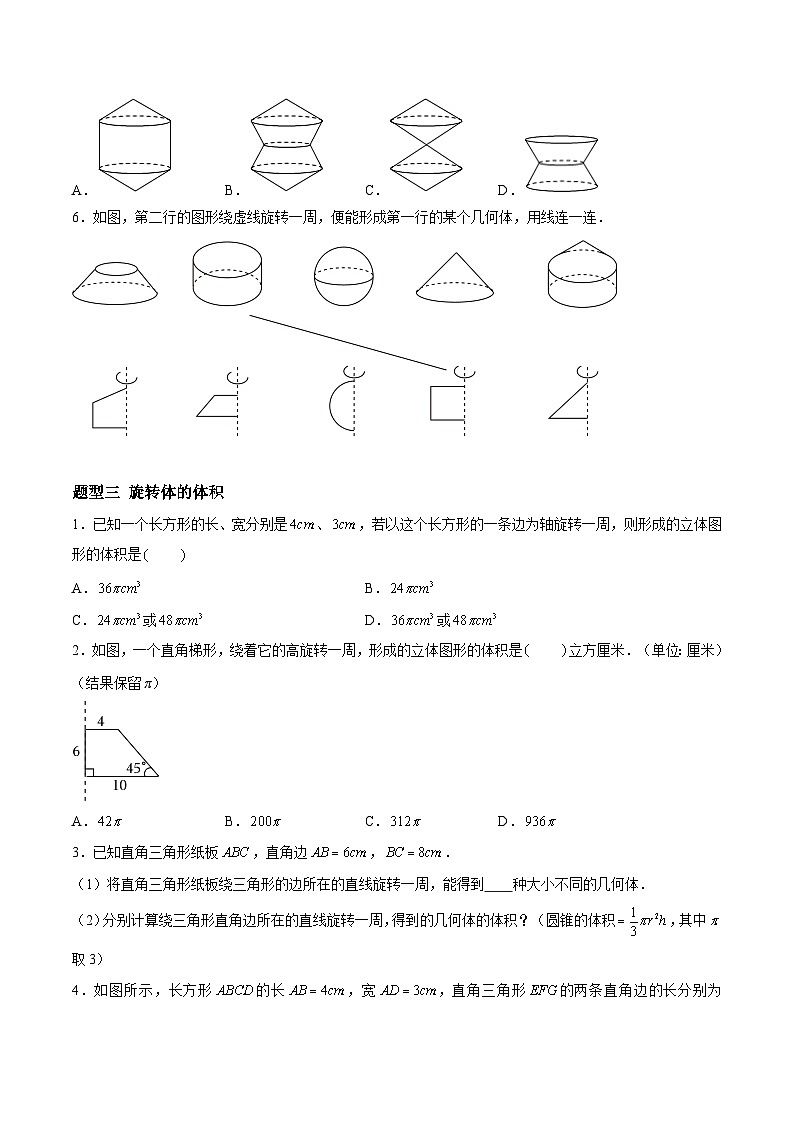
6．如图，第二行的图形绕虚线旋转一周，便能形成第一行的某个几何体，用线连一连．
【详解】解：如图所示：
．
题型三 旋转体的体积
1．已知一个长方形的长、宽分别是、，若以这个长方形的一条边为轴旋转一周，则形成的立体图形的体积是
A．B．
C．或D．或
【详解】解：①绕长所在的直线旋转一周得到圆柱体积为：；
②绕宽所在的直线旋转一周得到圆柱体积：．
故本题选：．
2．如图，一个直角梯形，绕着它的高旋转一周，形成的立体图形的体积是 立方厘米．（单位：厘米）（结果保留π）
A．B．C．D．
【详解】解：
（立方厘米），
答：形成的立体图形的体积是立方厘米．
故本题选：．
3．已知直角三角形纸板，直角边，．
（1）将直角三角形纸板绕三角形的边所在的直线旋转一周，能得到 种大小不同的几何体．
（2）分别计算绕三角形直角边所在的直线旋转一周，得到的几何体的体积？（圆锥的体积，其中取3）
【详解】解：（1）将直角三角形纸板绕三角形的三条边所在的直线旋转一周，能得到3种大小不同的几何体，
故本题答案为：3；
（2）以为轴：（立方厘米），
以为轴：（立方厘米），
答：以为轴得到的圆锥的体积是384立方厘米，以为轴得到的圆锥的体积是288立方厘米．
4．如图所示，长方形的长，宽，直角三角形的两条直角边的长分别为，，小明将两个图形中长度相等的边重合（两个图形无重叠），然后组合成新的图形，并将该图形绕它的最长边所在的直线旋转一周，求得到的几何体的体积．，
【详解】解：①当与重合时，
得到的几何体的体积为()；
②当与重合时，
得到的几何体的体积为()；
答：得到的几何体的体积或．
5．小军和小红分别以直角梯形的上底和下底为轴，将梯形旋转一周，得到的两个立体图形．
（1）你同意 的说法；
（2）为了研究你的猜想是否正确，你需要求出两个立体图形的体积，请列式计算甲、乙立体图形的体积并求出它们的比值是多少？
【详解】解：（1）两个立体图形的体积不相等，同意小红的说法，
故本题答案为：小红；
（2）甲的体积：，
乙的体积：，
甲、乙立体图形的体积并求出它们的比值是．
6．探究：有一长，宽的矩形纸板，现要求以其一组对边中点所在直线为轴，旋转，得到一个圆柱，现可按照两种方案进行操作：
方案一：以较长的一组对边中点所在直线为轴旋转，如图①；
方案二：以较短的一组对边中点所在直线为轴旋转，如图②．
（1）请通过计算说明哪种方法构造的圆柱体积大；
（2）如果该矩形的长宽分别是和呢？请通过计算说明哪种方法构造的圆柱体积大；
（3）通过以上探究，你发现对于同一个矩形（不包括正方形），以其一组对边中点所在直线为轴旋转得到一个圆柱，怎样操作所得到的圆柱体积大（不必说明原因）？
【详解】解：（1）方案一：，
方案二：，
，
方案一构造的圆柱的体积大；
（2）方案一：，
方案二：，
，
方案一构造的圆柱的体积大；
（3）由（1）、（2）得：以较长一组对边中点所在直线为轴旋转得到的圆柱的体积大．
题型四 图形变换
1．“飞流直下三千尺”、“坐地日行八万里（只考虑地球自转）”如果只从数学角度看，它们分别蕴含的图形变换是
A．平移、对称B．对称、旋转C．平移、旋转D．旋转、对称
【详解】解：根据平移和旋转定义可知：“飞流直下三千尺”是平移，“坐地日行八万里”是旋转．
故本题选：．
2．一个图形无论经过平移还是旋转，有以下说法：
（1）对应线段平行；
（2）对应线段相等；
（3）对应角相等；
（4）不改变图形的形状和大小，
其中正确的有
A．（1）（2）（3）B．（1）（2）（4）C．（1）（3）（4）D．（2） （4）
【详解】解：一个图形无论经过平移还是旋转，对应线段和角相等，不改变图形的形状和大小，旋转后对应的线段可能不平行．
故本题选：．
3．下列各组图形中，能将其中一个图形经过平移变换得到另一图形的是
A．B．
C．D．
【详解】解：．其中一个图形经过位似变换得到另一图形，不合题意；
．其中一个图形经过平移变换得到另一图形，符合题意；
．其中一个图形经过旋转变换得到另一图形，不合题意；
．其中一个图形经过轴对称变换得到另一图形，不合题意．
故本题选：．
4．对下列各表情图片的变换顺序描述正确的是
A．轴对称，平移，旋转B．轴对称，旋转，平移
C．旋转，轴对称，平移D．平移，旋转，轴对称
【详解】解：下列各表情图片的变换顺序是轴对称变换平移变换旋转变换．
故本题选：．
5．如图的四个图形中，通过翻折变换、旋转变换和平移变换都能得到的图形是
A．B．
C．D．
【详解】解：、图形只能通过旋转变换得到，故选项错误；
、图形通过翻折变换、旋转变换和平移变换都能得到，故选项正确；
、图形不能通过翻折变换、旋转变换和平移变换得到，故选项错误；
、图形只能通过平移变换得到，故选项错误．
故本题选：．
6．如图，图2是由图1经过平移得到的，图2还可以看作是由图1经过怎样的变换得到的？现给出两种变换方式：①2次旋转；②2次轴对称．下面说法正确的是
A．①②都不可行B．①②都可行C．只有①可行D．只有②可行
【详解】解：图2是由图1两次旋转得到，也是由图1两次轴对称变换得到．
故本题选：．
7．如图，在方格纸中的经过变换得到，正确的变换是
A．把向右平移6格
B．把向右平移4格，再向上平移1格
C．把绕着点顺时针旋转，再向右平移6格
D．把绕着点逆时针旋转，再向右平移6格
【详解】解：由图象可知：绕着点逆时针方向旋转与形状相同，向右平移6格就可以与重合．
故本题选：．
8．如图，在的方格纸中，小树从位置经过平移旋转后到达位置，下列说法中正确的是
A．先向右平移6格，再绕点顺时针旋转
B．先向右平移6格，再绕点逆时针旋转
C．先向右平移6格，再绕点顺时针旋转
D．先向右平移6格，再绕点逆时针旋转
【详解】解：小树经过正方形的顶点、，
，
小树从位置经过旋转平移后到位置时应绕点逆时针旋转，再向右平移6格．
故本题选：．
1．如图，长方形的相邻两边的长分别为、，将它分别绕相邻两边旋转一周．
（1）两次旋转所形成的几何体都是 ；
（2）若x＋y＝a（a是常数），分别记绕长度为、的边旋转一周的几何体的体积为，，其中、、的部分取值如表所示：
①通过表格中的数据计算： ， ， ；
②当逐渐增大时，的变化情况： ；
③当变化时，请直接写出与的大小关系．
【详解】解：（1）由圆柱的定义可知：旋转所得的几何体是圆柱，
故本题答案为：圆柱；
（2）圆柱的体积底面积高，
①当时，，解得：，∴，∴，
当时，，，
当时，，，
故本题答案为：10，，；
②，
当逐渐增大时，的变化为：先增大，后减小，
故本题答案为：先增大，后减小；
③，，
令Vy＝Vx，解得：x＝5，
∴当x＝5时，Vy＝Vx；当0＜x＜5时，Vy＜Vx；当5＜x＜10时，Vy＞Vx．1
2
3
4
5
6
7
8
9