2024-2025学年浙江省杭州市淳安县九年级（上）期中数学试卷 含详解

这是一份2024-2025学年浙江省杭州市淳安县九年级（上）期中数学试卷 含详解，共17页。试卷主要包含了下列事件中，属于随机事件的是，抛物线的顶点坐标是，，则等内容，欢迎下载使用。
1．（3分）下列关于的函数中，属于二次函数的是
A．B．C．D．
2．（3分）下列事件中，属于随机事件的是
A．掷一次骰子，朝上一面的点数大于0
B．从装有6个白球的袋中摸出一个红球
C．奥运射击冠军杨倩射击一次，命中靶心
D．明天太阳从西方升起
3．（3分）抛物线的顶点坐标是
A．B．C．D．
4．（3分）如图，四边形是的内接四边形，若，则的度数是
A．B．C．D．
5．（3分）某小组作“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的实验最有可能的是
A．掷一个质地均匀的正六面体骰子，向上的面点数是4
B．一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃
C．暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球
D．在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”
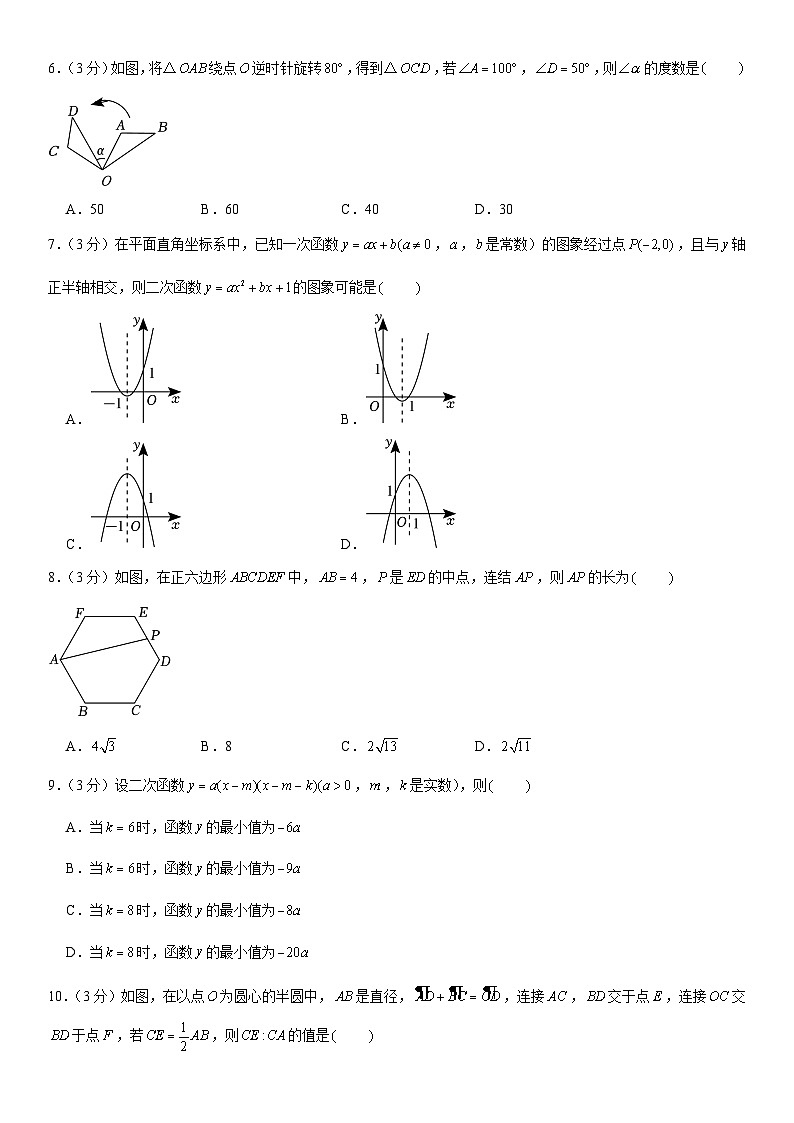
6．（3分）如图，将△绕点逆时针旋转，得到△，若，，则的度数是
A．50B．60C．40D．30
7．（3分）在平面直角坐标系中，已知一次函数，，是常数）的图象经过点，且与轴正半轴相交，则二次函数的图象可能是
A．B．
C．D．
8．（3分）如图，在正六边形中，，是的中点，连结，则的长为
A．B．8C．D．
9．（3分）设二次函数，，是实数），则
A．当时，函数的最小值为
B．当时，函数的最小值为
C．当时，函数的最小值为
D．当时，函数的最小值为
10．（3分）如图，在以点为圆心的半圆中，是直径，，连接，交于点，连接交于点，若，则的值是
A．B．C．D．
二.填空题：本大题有6个小题，每小题3分，共18分。
11．（3分）已知的面积为，若，则点与圆的位置关系是 ．
12．（3分）一个扇形的半径为6，圆心角为，则该扇形的面积是 ．
13．（3分）一个仅装有球的不透明布袋里共有6个红球和个白球（仅有颜色不同）．若从中任意摸出一个球是红球的概率为，则 ．
14．（3分）如图，已知一次函数，二次函数，为常数）两函数图象交于点，，当时，的取值范围为 ．
15．（3分）如图，△是的内接三角形，且是的直径，点为上的动点，且，的半径为6，则点到距离的最大值是 ．
16．（3分）设二次函数，、是常数），已知函数值和自变量的部分对应取值如表所示：
有以下结论：①函数图象的对称轴是直线；②若、都是正数，则的取值范围是且；③当时，恒有，则的取值范围是．其中正确的结论是 （只填序号）
三.解答题：本大题有8个小题，共72分.解答应写出文字说明、证明过程或演算步骤。
17．（8分）已知二次函数、为常数）的图象经过点，．
（1）求该二次函数的表达式和顶点坐标；
（2）当时，求的值．
18．（8分）旅客在网购高铁车票时，系统是随机分配座位的．小王和小李打算购买从杭州到北京的高铁车票（如图所示，同一排的座位编号为，，，，，假设系统已将两人分配到同一排后，在同一排分配各个座位的机会是均等的．
（1）求系统将王某安排到靠窗座位的概率；
（2）求系统分配给王某和李某相邻座位（过道两侧座位，不算相邻）的概率．
19．（8分）（1）如图①，是△的外接圆，，，求的半径．
（2）如图②，是△的外接圆，，是上一点．请你只用无刻度的直尺，画出图②中的平分线．（保留作图痕迹）
20．（8分）某书店销售儿童书刊，一天可售出20套，每套盈利40元，为了扩大销售，增加盈利，尽快减少库存，书店决定采取降价措施，若一套书每降价1元，平均每天可多售出2套．设每套书降价元时，书店一天可获利润元．
（1）求关于的函数解析式（化为一般形式）；
（2）当每套书降价多少元时，书店可获最大利润？最大利润为多少？
21．（8分）如图△中，，为的直径，，分别交于，，连接，．
（1）求证：；
（2）如果，，求的长．
22．（10分）综合与实践
素材1：一年一度的科技节即将到来，小明所在的科技小组研制了一种航模飞机．通过多次实验，收集了飞机的水平飞行距离（单位：与相对应的飞行高度（单位：的数据（如表）
素材2：如图，活动小组在水平安全线上处设置一个高度可以变化的发射平台试飞航模飞机，已知航模的飞行高度（单位：与水平飞行距离（单位：满足二次函数关系．
任务1：请求出关于的函数关系式（不用写自变量的取值范围），并求出航模的最远飞行距离；
任务2：在安全线上设置回收区域，点的右侧为回收区域（包括端点，．若飞机落在回收区域内，求发射平台相对于安全线的最低高度．
23．（10分）已知二次函数，是实数，．
（1）求证：若该函数图象与轴一定有两个不同的交点；
（2）若，，该函数图象经过，两点，若，分别位于抛物线对称轴的两侧，且，求的取值范围．
（3）若该二次函数满足当时，总有随的增大而减小，且过点，求的最小值．
24．（12分）如图1，已知四边形内接于，，延长到，使，连接，是的中点，连接．（1）若的半径为2，，求劣弧的长；
（2）如图2，连接，求证：；
（3）如图3，是的中点，过作的垂线交于点，连接，，求证：．
2024-2025学年浙江省杭州市淳安县九年级（上）期中数学试卷
参考答案
一.选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。
1．【解答】解：、是二次函数，故此选项符合题意；
、是一次函数，故此选项不符合题意；
、是反比例函数，故此选项不符合题意；
、是正比例函数，故此选项不符合题意；
故选：．
2．【解答】解：、是必然事件，不符合题意；
、不可能事件，不符合题意；
、是随机事件，符合题意；
、是不可能事件，不符合题意；
故选：．
3．【解答】解：抛物线，
当时，，
抛物线的顶点坐标是，
故选：．
4．【解答】解：，
，
四边形是的内接四边形，
，
故选：．
5．【解答】解：、掷一个质地均匀的正六面体骰子，向上的面点数是4的概率为，故符合题意；
、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃的概率是：；故不符合题意；
、暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球的概率为，故不符合题意；
、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”的概率为，故不符合题意．
故选：．
6．【解答】解：将△绕点逆时针旋转，
，，
，
，，，
，
解得，
故选：．
7．【解答】解：一次函数，，是常数）的图象经过点，且与轴正半轴相交，
，，
，
抛物线开口向上，对称轴为直线，
故选：．
8．【解答】解：如图，过点作，垂足为，由正六边形的对称性可知，，正六边形的中心在上，连接，
点是正六边形的中心，
，
在△中，，，
，
，
在△中，，，
，
故选：．
9．【解答】解：令，则，
，．
二次函数与轴的交点坐标是，．
二次函数的对称轴是：直线．
，
有最小值．
当时，最小，
即
，
当时，函数的最小值为；
当时，函数的最小值为．
综上，选项正确，其余选项错误．
故选：．
10．【解答】解：连接、．
设，，，
则，
，
，
，
，
，
，，
，
在△中利用勾股定理，得，
．
故选：．
二.填空题：本大题有6个小题，每小题3分，共18分。
11．【解答】解：的面积为，
的半径，
，
点在内．
故答案为：点在内．
12．【解答】解：一个扇形的半径为6，圆心角为，
该扇形的面积是：，
故答案为：．
13．【解答】解：由题意得，
，
解得，
经检验是所列分式方程的根，
，
故答案为：2．
14．【解答】解：将代入得，
将代入得，
解得，
抛物线经过点，，
由图象可得时，抛物线在直线上方，
时的取值范围是．
故答案为：．
15．【解答】解：过作于，延长交于，
则此时，点到的距离最大，且点到距离的最大值，
，，的半径为6，
，
，
，
则点到距离的最大值是，
故答案为：．
16．【解答】解：，在抛物线上，
函数图象的对称轴是直线，
故①错误，不符合题意；
，在抛物线上，
，
解得，
抛物线为，
、都是正数，，在抛物线上，
，
解得，
，
且，
故②正确，符合题意；
当时，当时，恒有，
当时，函数最小值，
解得，
取值范围是，
当时，如图，
当时，恒有，
综上，当时，恒有，则的取值范围是且，
故③错误，不符合题意．
故答案为：②．
三.解答题：本大题有8个小题，共72分.解答应写出文字说明、证明过程或演算步骤。
17．【解答】解：（1）二次函数、为常数）的图象经过点，．
，
该二次函数的表达式，
，
顶点坐标；
（2）当时，，
即，
解得，，
当时，的值为5或．
18．【解答】解：（1）系统将王某安排到靠窗座位的概率为；
（2）根据题意画树状图如下：
由树状图可知，共有20种等情况数，其中相邻坐位的情况数有6种，
则系统分配给王某和李某相邻座位（过道两侧座位，不算相邻）的概率是．
19．【解答】解：（1）连接并延长交于点，连接，
，
，
，
，，
，，
，
设的半径为，
则在△中，，，，
所以，
解得．
答：的半径为6.25；
（2）如图，就是的平分线．
20．【解答】解：（1）设每套书降价元时，所获利润为元，则每天可出售套．
由题意得：．
（2），
，
当时，取得最大值1250；
即当将价15元时，该书店可获得最大利润，最大利润为1250元．
21．【解答】（1）证明：连接，
为的直径，
，
，
，
，
；
（2）解：，，
，
在△中，，
，
为的直径，
，
△的面积，
，
，
解得：．
22．【解答】解：任务1：由题意，根据所给表格数据，可得抛物线的对称轴是直线，
顶点为．
故，
将代入到，
，
，
又令，
，
（舍去）或，
故航模的最远飞行距离为；
任务2：设发射平台相对于安全线的高度为，
飞机相对于安全线的飞行高度为：，
当时，，
则，
解得，
发射平台相对于安全线的最低高度为．
23．【解答】（1）证明：，△，
该函数图象与轴一定有两个不同的交点；
（2）解：若，则抛物线的对称轴为直线，
，若，分别位于抛物线对称轴的两侧，且，
则且，
解得：，
的取值范围是；
（3）解：图象过点，
则，则，
当时，总有随的增大而减小，
则，，
则，
，函数的对称轴为直线，
故当时，函数取得最小值为2，
即的最小值是2．
24．【解答】（1）解：连接，，如图1，
四边形是的内接四边形，
，
，
，
，
劣弧的长；
（2）证明：如图2，连接，，，
，
，
，
，，
是△的中位线，
，
，
；
（3）证明：如图3中，连接．
，，
是△的中位线，
，
，
，
，
是的中点，
，
，
，
，
，
，
△△，
．
0
1
1
窗
过道
窗
飞行水平距离（单位：
0
20
40
60
80
100
飞行高度（单位：
0
40
64
72
64
40