



所属成套资源:备战2025年高考数学一轮专题复习全套考点突破和专题检测40专题
- 专题11 导数的概念、运算及几何意义9题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测 试卷 0 次下载
- 专题12 导数的应用--函数的单调性问题5题型分类练习-备战2025年高考数学一轮专题复习全套考点突破和专题检测 试卷 0 次下载
- 专题14 导数的应用--函数的最值问题5题型分类练习-备战2025年高考数学一轮专题复习全套考点突破和专题检测 试卷 0 次下载
- 专题15 导数的应用--函数的零点问题5题型分类练习-备战2025年高考数学一轮专题复习全套考点突破和专题检测 试卷 0 次下载
- 专题16 任意角与弧度制及三角函数的概念6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测 试卷 0 次下载
专题13 导数的应用--函数的极值问题5题型分类练习-备战2025年高考数学一轮专题复习全套考点突破和专题检测
展开
这是一份专题13 导数的应用--函数的极值问题5题型分类练习-备战2025年高考数学一轮专题复习全套考点突破和专题检测,文件包含专题13导数的应用--函数的极值问题5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测原卷版docx、专题13导数的应用--函数的极值问题5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测解析版docx等2份试卷配套教学资源,其中试卷共93页, 欢迎下载使用。
1、函数的极值
函数在点附近有定义,如果对附近的所有点都有,则称是函数的一个极大值,记作.如果对附近的所有点都有,则称是函数的一个极小值,记作.极大值与极小值统称为极值,称为极值点.
求可导函数极值的一般步骤
(1)先确定函数的定义域;
(2)求导数;
(3)求方程的根;
(4)检验在方程的根的左右两侧的符号,如果在根的左侧附近为正,在右侧附近为负,那么函数在这个根处取得极大值;如果在根的左侧附近为负,在右侧附近为正,那么函数在这个根处取得极小值.
注:①可导函数在点处取得极值的充要条件是:是导函数的变号零点,即,且在左侧与右侧,的符号导号.
②是为极值点的既不充分也不必要条件,如,,但不是极值点.另外,极值点也可以是不可导的,如函数,在极小值点是不可导的,于是有如下结论:为可导函数的极值点;但为的极值点.
一、单选题
1.(2024·全国)若是函数的极值点,则的极小值为.
A.B.C.D.
【答案】A
【详解】由题可得,
因为,所以,,故,
令,解得或,
所以在上单调递增,在上单调递减,
所以的极小值为,故选A.
【名师点睛】(1)可导函数y=f(x)在点x0处取得极值的充要条件是f ′(x0)=0,且在x0左侧与右侧f ′(x)的符号不同;
(2)若f(x)在(a,b)内有极值,那么f(x)在(a,b)内绝不是单调函数,即在某区间上单调增或减的函数没有极值.
2.(2024高二下·安徽亳州·期末)设函数一定正确的是( )
A.B.
C.D.
【答案】D
【详解】对于A选项函数的极大值不一定是函数的最大值,所以错;对于B中的是将的图象关于y轴对称,所以是其极大值点,错误;对于C中的是将的图象关x轴对称,所以才是其极小值点,错误;而对于D中的是将的图象关原点对称,故是其极小值点,正确.
故选D.
3.(2024高三上·全国·单元测试)设,若为函数的极大值点,则( )
A.B.C.D.
【答案】D
【分析】
先考虑函数的零点情况,注意零点左右附近函数值是否变号,结合极大值点的性质,对进行分类讨论,画出图象,即可得到所满足的关系,由此确定正确选项.
【详解】若,则为单调函数,无极值点,不符合题意,故.
有和两个不同零点,且在左右附近是不变号,在左右附近是变号的.依题意,a为函数的极大值点,在左右附近都是小于零的.
当时,由,,画出的图象如下图所示:
由图可知,,故.
当时,由时,,画出的图象如下图所示:
由图可知,,故.
综上所述,成立.
故选:D
【点睛】本小题主要考查三次函数的图象与性质,利用数形结合的数学思想方法可以快速解答.
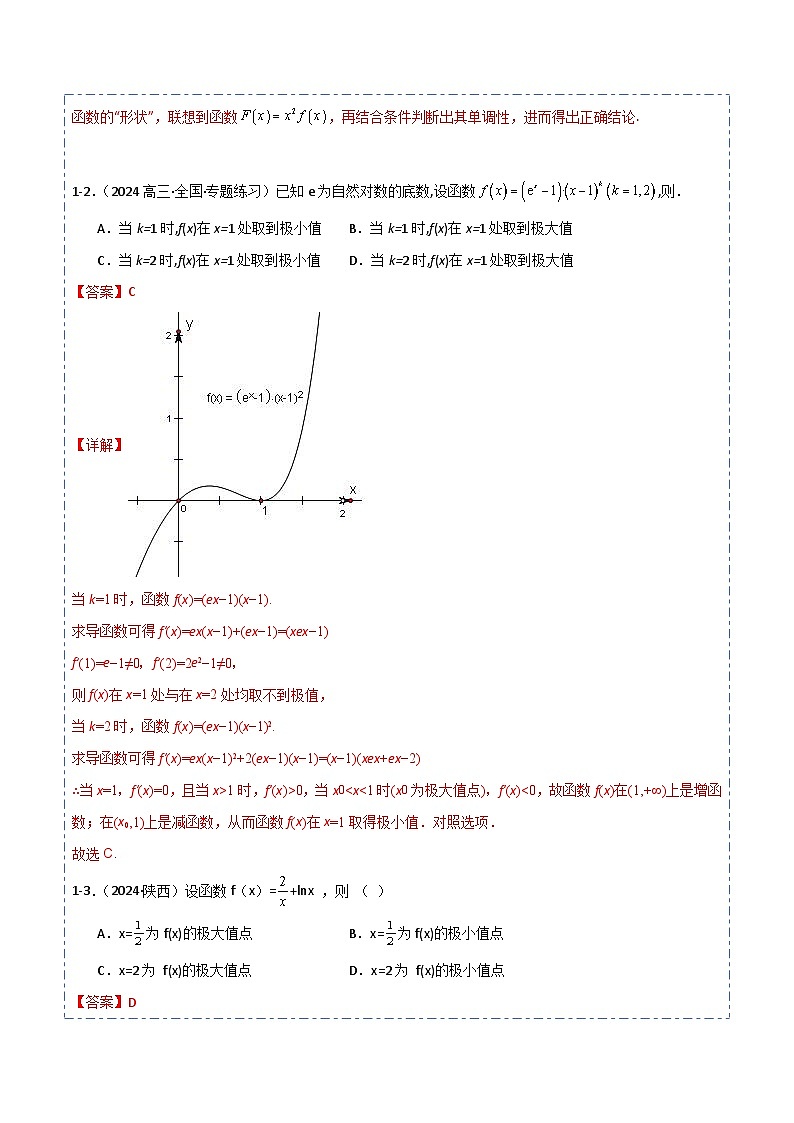
4.(2024高三·全国·课后作业)已知函数f(x)=x(lnx-ax)有两个极值点,则实数a的取值范围是( )
A.(-∞,0)B.C.(0,1)D.(0,+∞)
【答案】B
【详解】函数f(x)=x(lnx﹣ax),则f′(x)=lnx﹣ax+x(﹣a)=lnx﹣2ax+1,
令f′(x)=lnx﹣2ax+1=0得lnx=2ax﹣1,
函数f(x)=x(lnx﹣ax)有两个极值点,等价于f′(x)=lnx﹣2ax+1有两个零点,
等价于函数y=lnx与y=2ax﹣1的图象有两个交点,
在同一个坐标系中作出它们的图象(如图)
当a=时,直线y=2ax﹣1与y=lnx的图象相切,
由图可知,当0<a<时,y=lnx与y=2ax﹣1的图象有两个交点.
则实数a的取值范围是(0,).
故选B.
5.(2024·吉林通化·模拟预测)已知函数在区间上的最大值为k,则函数在上( )
A.有极大值,无最小值B.无极大值,有最小值
C.有极大值,有最大值D.无极大值,无最大值
【答案】D
【分析】利用导函数研究单调性,结合区间最值求得,进而判断在上的单调性,即可得答案.
【详解】由,则时,时,
所以在上递增,上递减,
而,在上的最大值为k,
所以,即,此时在上递减,且无极大值和最大值.
故选:D
6.(2024高二下·河北秦皇岛·期末)已知是函数的导函数,若函数的图象大致如图所示,则极值点的个数为( )
A.1B.2C.3D.4
【答案】B
【分析】根据函数图象得到的取值情况,即可得到的单调性,即可得到极值点数.
【详解】由图可知,当时,,即在上单调递减;
当时,,即在上单调递增;
当时,,即在上单调递增;
当时,,即在上单调递减.
所以在处取得极小值,在处取得极大值,
故极值点的个数为.
故选:B
7.(2024高三上·陕西渭南·阶段练习)已知函数的导函数的图象如图所示,则下列结论中正确的是( )
A.是函数的极小值点
B.是函数的极大值点
C.函数在上单调递增
D.函数在处的切线斜率小于零
【答案】C
【分析】根据导函数图象,求得函数单调性,结合极值点定义,即可容易判断选择.
【详解】由图象得时,,时,,
故在单调递减,在单调递增,
故是函数的极小值点,即选项A、B错误,C正确;
对选项D:显然,故D错误.
故选:C.
8.(2024·陕西)对二次函数(为非零整数),四位同学分别给出下列结论,其中有且仅有一个结
论是错误的,则错误的结论是
A.是的零点B.1是的极值点
C.3是的极值D.点在曲线上
【答案】A
【详解】若选项A错误时,选项B、C、D正确,,因为是的极值点,是的极值,所以,即,解得:,因为点在曲线上,所以,即,解得:,所以,,所以,因为,所以不是的零点,所以选项A错误,选项B、C、D正确,故选A.
【考点定位】1、函数的零点;2、利用导数研究函数的极值.
9.(2024高三上·陕西汉中·阶段练习)已知函数,则的极小值为( )
A.B.C.D.
【答案】A
【分析】根据给定条件,利用导数求出函数极小值作答.
【详解】函数的定义域为,
求导得,
,,则由,得或,由,得,
因此函数在上单调递减,在上单调递增,则当时,取得极小值,
所以函数的极小值为.
故选:A
10.(2024高三·全国·专题练习)函数的大致图像如图所示,,是函数的两个极值点,则等于( )
A.B.C.D.
【答案】C
【分析】先根据图象求出函数的解析式,再求得,将已知条件,是函数的两个极值点转化为,是的两个根,再根据韦达定理求解即可.
【详解】因为函数的图像过原点,所以.
又,即,解得,
所以,则,
又,是函数的两个极值点,
所以,是的两个根,
所以,,
所以.
故选:C.
11.(2024高二下·吉林长春·阶段练习)已知实数成等比数列,且曲线的极大值点为,极大值为,则等于( )
A.2B.C.D.1
【答案】A
【分析】根据实数成等比数列,可得.利用导数研究函数的单调性与极值,进而得出结论.
【详解】因为实数成等比数列,所以,
由,得,
令,解得,
当或时,,当时,,
所以函数在上单调递减;函数在上单调递增;函数在上单调递减.
所以时,函数取得极小值,时,函数取得极大值.
因为曲线的极大值点为,极大值为,
所以,,即.
所以,所以,
故选:A.
12.(2024高二下·新疆昌吉·期末)如图是函数的导函数的图象,给出下列命题:
①x=-2是函数的极值点;
②x=1是函数的极值点;
③的图象在处切线的斜率小于零;
④函数在区间上单调递增.
则正确命题的序号是( )
A.①②B.②④C.②③D.①④
【答案】D
【分析】根据导数的几何意义,与函数的单调性,极值点的关系,结合图象即可作出判断.
【详解】对于①,根据导函数图像可知,-2是导函数的零点,且-2的左右两侧导函数值符号异号,故-2是极值点,故①正确;
对于②,1不是极值点,因为1的左右两侧导函数符号一致,故②错误;
对于③,0处的导函数值即为此点的切线斜率显然为正值,故③错误;
对于④,导函数在恒大等于零,故为函数的增区间,故④正确.
故选:D
【点睛】根据导函数和原函数的关系很容易分析单调性,然后要注意对极值点的理解,极值点除了是导函数得解还一定要保证在导函数值在此点两侧异号.
13.(2024高二下·全国·期中)已知函数的导函数的图像如图所示,则下列结论正确的是( )
A.是的极小值点B.是的极小值点
C.在区间上单调递减D.曲线在处的切线斜率小于零
【答案】D
【分析】根据导函数图像,求得函数单调性,结合极值点定义,即可判断ABC选项,根据导数的定义和几何意义即判断D选项,从而得出答案.
【详解】由图像知,当或时,,单调递增,
当时,,单调递减,
所以在区间,内单调递增,在区间内单调递减,
是的极大值点,3是的极小值点,故ABC错误;
又因为,所以曲线在处切线斜率小于零,故D正确.
故选:D.
14.(2024高三上·湖北武汉·阶段练习)若函数存在一个极大值与一个极小值满足,则至少有( )个单调区间.
A.3B.4C.5D.6
【答案】B
【分析】根据单调性与极值之间的关系分析判断.
【详解】若函数存在一个极大值与一个极小值,则至少有3个单调区间,
若有3个单调区间,
不妨设的定义域为,若,其中可以为,可以为,
则在上单调递增,在上单调递减,(若定义域为内不连续不影响总体单调性),
故,不合题意,
若,则在上单调递减,在上单调递增,有,不合题意;
若有4个单调区间,
例如的定义域为,则,
令,解得或,
则在上单调递增,在上单调递减,
故函数存在一个极大值与一个极小值,且,满足题意,此时有4个单调区间,
综上所述:至少有4个单调区间.
故选:B.
15.(2024高三·全国·专题练习)已知定义在R上的函数f(x),其导函数的大致图象如图所示,则下列叙述正确的是( )
A.
B.函数在x=c处取得最大值,在处取得最小值
C.函数在x=c处取得极大值,在处取得极小值
D.函数的最小值为
【答案】C
【分析】根据导函数的图象确定的单调性,从而比较函数值的大小及极值情况,对四个选项作出判断.
【详解】由题图可知,当时,,所以函数在上单调递增,
又a1,则当时,;
当时,.
所以在x=1处取得极小值.
若,则当时,,
所以.
所以1不是的极小值点.
综上可知,a的取值范围是.
方法二:.
(1)当a=0时,令得x=1.
随x的变化情况如下表:
∴在x=1处取得极大值,不合题意.
(2)当a>0时,令得.
①当,即a=1时,,
∴在上单调递增,
∴无极值,不合题意.
②当,即01满足题意.
(3)当a,则当x∈(,2)时,f ′(x)0.
所以f (x)0,当x0
相关试卷
这是一份专题12 导数的应用--函数的单调性问题5题型分类练习-备战2025年高考数学一轮专题复习全套考点突破和专题检测,文件包含专题12导数的应用--函数的单调性问题5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测原卷版docx、专题12导数的应用--函数的单调性问题5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测解析版docx等2份试卷配套教学资源,其中试卷共97页, 欢迎下载使用。
这是一份备战2025年高考数学一轮专题复习全套考点突破和专题检测专题15导数的应用--函数的零点问题5题型分类练习(原卷版+解析),共157页。试卷主要包含了函数零点问题的常见题型,函数零点的求解与判断方法,利用导数研究零点问题等内容,欢迎下载使用。
这是一份备战2025年高考数学一轮专题复习全套考点突破和专题检测专题14导数的应用--函数的最值问题5题型分类练习(原卷版+解析),共99页。试卷主要包含了函数的最值,不等式的恒成立与能成立问题,1);等内容,欢迎下载使用。








