专题35 空间向量的概念与运算5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测

这是一份专题35 空间向量的概念与运算5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测，文件包含专题35空间向量的概念与运算5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测原卷版docx、专题35空间向量的概念与运算5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测解析版docx等2份试卷配套教学资源，其中试卷共118页， 欢迎下载使用。

1．空间向量的有关概念
2.空间向量的有关定理
(1)共线向量定理：对任意两个空间向量a，b(b≠0)，a∥b的充要条件是存在实数λ，使a＝λb.
(2)共面向量定理：如果两个向量a，b不共线，那么向量p与向量a，b共面的充要条件是存在唯一的有序实数对(x，y)，使p＝xa＋yb.
(3)空间向量基本定理
如果三个向量a，b，c不共面，那么对任意一个空间向量p，存在唯一的有序实数组(x，y，z)，使得p＝xa＋yb＋zc，{a，b，c}叫做空间的一个基底．
3．空间向量的数量积及运算律
(1)数量积
非零向量a，b的数量积a·b＝|a||b|cs〈a，b〉．
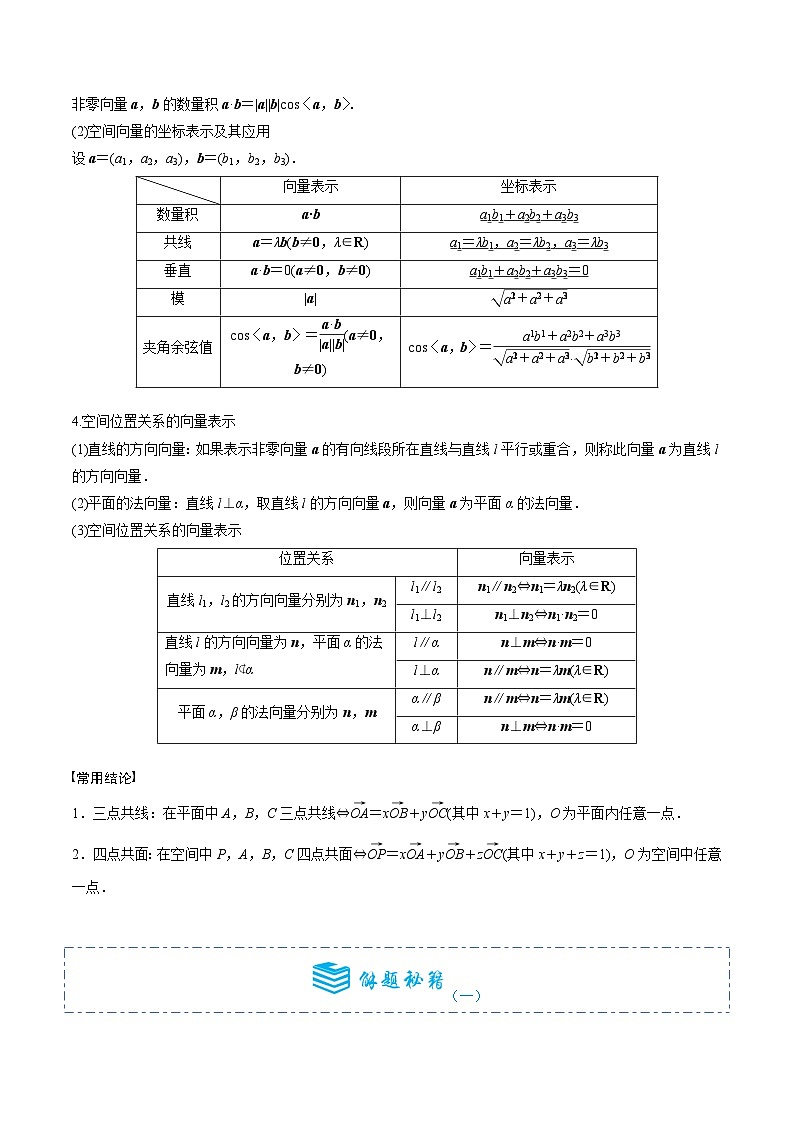
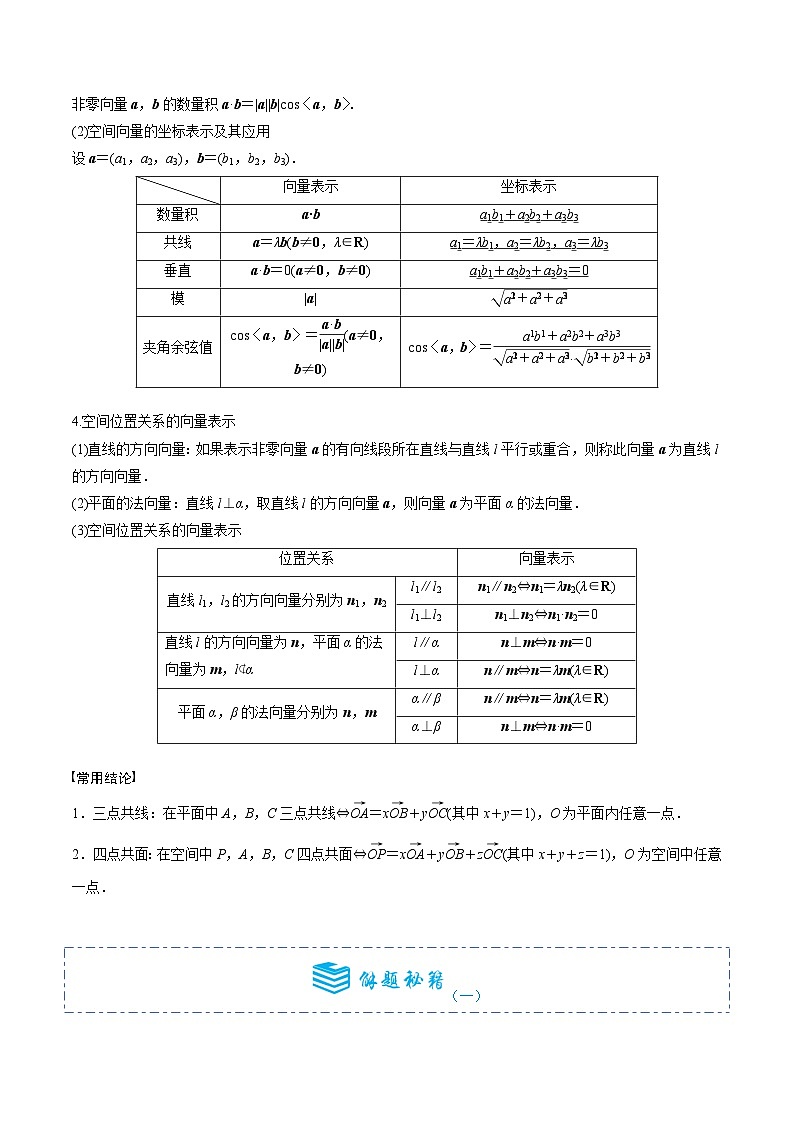
(2)空间向量的坐标表示及其应用
设a＝(a1，a2，a3)，b＝(b1，b2，b3)．
4.空间位置关系的向量表示
(1)直线的方向向量：如果表示非零向量a的有向线段所在直线与直线l平行或重合，则称此向量a为直线l的方向向量．
(2)平面的法向量：直线l⊥α，取直线l的方向向量a，则向量a为平面α的法向量．
(3)空间位置关系的向量表示
常用结论
1．三点共线：在平面中A，B，C三点共线⇔eq \(OA,\s\up6(→))＝xeq \(OB,\s\up6(→))＋yeq \(OC,\s\up6(→))(其中x＋y＝1)，O为平面内任意一点．
2．四点共面：在空间中P，A，B，C四点共面⇔eq \(OP,\s\up6(→))＝xeq \(OA,\s\up6(→))＋yeq \(OB,\s\up6(→))＋zeq \(OC,\s\up6(→))(其中x＋y＋z＝1)，O为空间中任意一点．
一、单选题
1．（2024高二下·江苏泰州·期中）若点，，在同一条直线上，则（ ）
A．21B．4C．4D．10
2．（2024高二上·山东菏泽·阶段练习）对于空间任意一点和不共线的三点，有如下关系：，则（ ）
A．四点必共面B．四点必共面
C．四点必共面D．五点必共面
3．（2024高二上·陕西商洛·阶段练习）已知，则下列向量中与平行的是（ ）
A．B．C．D．
4．（2024高二上·北京西城·期中）两个不同的平面和，平面的一个法向量为，平面的一个法向量，则平面与平面（ ）
A．平行B．垂直C．相交D．不能确定
5．（2024高二·全国·课后作业）下面关于空间向量的说法正确的是（ ）
A．若向量平行，则所在直线平行
B．若向量所在直线是异面直线，则不共面
C．若A，B，C，D四点不共面，则向量，不共面
D．若A，B，C，D四点不共面，则向量，，不共面
6．（2024高二上·安徽阜阳·阶段练习）下列命题中是假命题的是（ ）
A．任意向量与它的相反向量不相等
B．和平面向量类似，任意两个空间向量都不能比较大小
C．如果，则
D．两个相等的向量，若起点相同，则终点也相同
7．（2024高二上·浙江台州·阶段练习）已知平面的法向量为，，则直线和平面的位置关系是（ ）
A．B．C．与相交但不垂直D．
8．（2024高二上·全国·课后作业）若空间中任意四点O，A，B，P满足，其中m＋n＝1，则（ ）
A．P∈ABB．P∉AB
C．点P可能在直线AB上D．以上都不对
9．（2024高二上·全国·课后作业）已知在空间单位正交基底下，是空间的一组单位正交基底，是空间的另一组基底.若向量在基底下的坐标为，则向量在基底下的坐标为（ ）
A．B．C．D．
10．（2024高二上·新疆和田·期中）已知、分别为不重合的两直线、的方向向量，、分别为不重合的两平面、的法向量，则下列所有正确结论（ ）个.
①；②；③；④.
A．B．C．D．
11．（2024·福建福州·三模）以下四组向量在同一平面的是（ ）
A．、、B．、、
C．、、D．、、
12．（2024高二上·云南昆明·期末）如图，M在四面体OABC的棱BC的中点，点N在线段OM上，且，设，，，则下列向量与相等的向量是（ ）
A．B．
C．D．
13．（2024高三上·广东广州·阶段练习）如图所示的木质正四棱锥模型，过点A作一个平面分别交于点E，F，G，若，则的值为（ ）
A．B．C．D．
14．（2024·江西·二模）在四棱锥中，棱长为2的侧棱垂直底面边长为2的正方形，为棱的中点，过直线的平面分别与侧棱、相交于点、，当时，截面的面积为（ ）
A．B．2C．D．3
二、多选题
15．（2024高二下·浙江·期中）空间直角坐标系中，已知，，，，则（ ）
A．
B．是等腰直角三角形
C．与平行的单位向量的坐标为或
D．在方向上的投影向量的坐标为
16．（2024·广东佛山·二模）四面体中，，，，，，平面与平面的夹角为，则的值可能为（ ）
A．B．C．D．
三、填空题
17．（2024·上海金山·二模）已知向量，向量，则与的夹角的大小为 .
18．（2024高二上·北京西城·期中）已知平面的法向量为，平面的法向量为，若，则 ．
19．（2024高二上·山西·开学考试）已知直线的方向向量是，平面的法向量是，与的位置关系为 .
20．（2024高二下·天津蓟州·期中）已知点A（1，2，3），B（0，1，2），C（﹣1，0，λ），若A，B，C三点共线，则 ．
21．（2024高二上·湖南株洲·阶段练习）已知向量，若，则 ．
22．（2024高二上·北京·期中）直线的方向向量为，直线的方向向量为，平面的法向量为，，，则、、的值依次为 .
23．（2024高二上·浙江台州·阶段练习）如图，三棱锥中，平面ABC，，且，．若D是棱PC上的点，满足，且，则 ．
24．（2024高二上·江西宜春·阶段练习）如图所示，在正方体中，E是棱DD1的三等分点（靠近点），点F在棱C1D1上，且，若∥平面，则 .
四、解答题
25．（2024高三·全国·专题练习）如图，在四棱锥中，底面，底面是矩形，，分别是的中点，.证明：.
26．（2024高二下·江苏·课后作业）在正方体中，分别是的中点，试建立适当的空间直角坐标系，求证：平面平面.
27．（2024高一·全国·专题练习）如图所示，正四棱的底面边长1，侧棱长4，中点为，中点为．求证：平面平面.

28．（2024高三·全国·对口高考）如图所示的几何体中，四边形是等腰梯形，，，平面，，.

(1)求二面角的余弦值；
(2)在线段AB（含端点）上，是否存在一点P，使得平面.若存在，求出的值；若不存在，请说明理由.
29．（2024高一·全国·专题练习）如图，且，，且，且，平面ABCD，.若M为CF的中点，N为EG的中点，求证：平面CDE；
30．（2024高二上·广东广州·阶段练习）如图，在正方体中，E，F分别是，的中点．
(1)求证：；
(2)求证：平面
31．（2024高二下·江苏·课后作业）已知棱长为1的正方体在空间直角坐标系中的位置如图所示，分别为棱的中点，求证：.
32．（2024高二·全国·专题练习）如图所示，平面平面，四边形为正方形，是直角三角形，且，，，分别是线段，，的中点，求证：平面平面．
33．（2024高三·全国·专题练习）如图，在几何体ABCDE中，ABC，BCD，CDE均为边长为2的等边三角形，平面ABC⊥平面BCD，平面DCE⊥平面BCD．求证：A，B，D，E四点共面；
34．（2024高三·全国·专题练习）如图，直三棱柱中，，，，D为BC的中点，E为上的点，且．求证：平面；
35．（2024高三·全国·专题练习）如图，直三棱柱的侧面为正方形，，E，F分别为，的中点，．证明：平面；
36．（2024高三·全国·专题练习）在正方体中，如图、分别是，的中点．求证：平面平面；
37．（2024高二·全国·专题练习）如图，正三棱柱中，分别是棱上的点，.

证明：平面平面.
38．（2024高三·全国·专题练习）已知直三棱柱中，侧面为正方形，，E，F分别为AC和的中点，D为棱上的动点..证明：；
39．（2024高三·全国·专题练习）如图，在四棱锥中，底面ABCD是菱形，，，，底面ABCD，，点E在棱PD上，且.证明：平面平面ACE；
40．（2024高三·全国·专题练习）如图，在三棱柱中，平面ABC，，，D为的中点，交于点E．证明：.
41．（2024高三·全国·专题练习）如图，在底面是矩形的四棱锥中，平面，，，是PD的中点.
求证：平面平面.
42．（2024高三·全国·专题练习）如图，棱台中，，底面ABCD是边长为4的正方形，底面是边长为2的正方形，连接，BD，.证明：.
43．（2024·云南曲靖·模拟预测）如图，已知四棱锥的底面是平行四边形，侧面是等边三角形，.
(1)求证：平面平面；
(2)设为侧棱上一点，四边形是过两点的截面，且平面，是否存在点，使得平面平面？若存在，求的值；若不存在，说明理由.
44．（2024高三·全国·专题练习）斜三棱柱的各棱长都为，点在下底面的投影为的中点.在棱（含端点）上是否存在一点使？若存在，求出的长；若不存在，请说明理由；
45．（2024高三·全国·专题练习）斜三棱柱的各棱长都为2，，点在下底面ABC的投影为AB的中点O．在棱（含端点）上是否存在一点D使？若存在，求出BD的长；若不存在，请说明理由；
46．（2024·河北保定·一模）如图，平行六面体的所有棱长均为，底面为正方形，，点为的中点，点为的中点，动点在平面内．
(1)若为中点，求证：；
(2)若平面，求线段长度的最小值．
47．（2024高二上·北京海淀·期中）已知三棱锥（如图1）的平面展开图（如图2）中，四边形为边长为的正方形，和均为正三角形.在三棱锥中：
(1)求点到平面的距离；
(2)若点在棱上，满足，点在棱上，且，求的取值范围.
48．（2024高三·全国·专题练习）如图，在四棱锥中，底面ABCD为正方形，平面ABCD，E为PD的中点，.求证：PB平面AEC；
49．（2024高二上·山东聊城·阶段练习）如图，正方形与梯形所在平面互相垂直，已知，，．

(1)求证：平面．
(2)线段上是否存在点M，使平面平面？若存在，求出的值；若不存在，请说明理由．
50．（2024高二·阶段练习）如图，在四棱锥中，平面，，，，点为棱的中点．证明：

(1)平面；
(2)平面⊥平面．
51．（2024高三·全国·专题练习）在苏州博物馆有一类典型建筑八角亭，既美观又利于采光，其中一角如图所示，为多面体，，，，底面，四边形是边长为2的正方形且平行于底面，，，的中点分别为，，，．证明：//平面；

52．（2024高二上·广东佛山·阶段练习）如图，在正方体中，分别是的中点

(1)证明：平面.
(2)在直线上是否存在点，使得平面？若存在，请指出的位置；若不存在.请说明理由.
53．（2024高三·全国·专题练习）在四棱锥中，平面ABCD⊥平面PCD，底面ABCD为梯形．，，且，，．若M是棱PA的中点，则对于棱BC上是否存在一点F，使得MF与PC平行．

54．（2024高二上·山西大同·期中）如图，在直三棱柱中，，垂足为，为线段上的一点.

(1)若为线段的中点，证明：平面；
(2)若平面平面，求的值.
55．（2024高二下·江苏·课后作业）如图，四边形ABCD和ABEF都是平行四边形，且不共面，M，N分别是AC，BF的中点，求证：.
56．（2024高二·全国·课后作业）如图，在平行六面体中，，．
(1)求证：、、三点共线；
(2)若点是平行四边形的中心，求证：、、三点共线．
57．（2024高二上·湖北宜昌·期中）如图，在棱长为2的正方体中，点分别是线段的中点.

(1)求证：
(2)求三棱锥的体积.
58．（2024高三·全国·专题练习）如图四棱锥，且，平面平面，且是以为直角的等腰直角三角形，其中为棱的中点，点在棱上，且.求证：四点共面.
59．（2024高二上·河北邢台·阶段练习）如图，在边长为3的正方体中，点P，Q，R分别在棱，，上，且.
（1）求点D到平面的距离；
（2）若平面与线段的交点为N，求的值.
60．（2024高三·全国·专题练习）已知E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，用向量法证明：
(1)E，F，G，H四点共面；
(2)平面EFGH．
61．（2024·四川泸州·模拟预测）如图，四边形为正方形，若平面平面，，，.
(1)求二面角A－CF－D的余弦值；
(2)判断点D与平面CEF的位置关系，并说明理由.
62．（2024·河南郑州·一模）如图，正四棱锥的底面边长和高均为2，，分别为，的中点．
(1)若点是线段上的点，且，判断点是否在平面内，并证明你的结论；
(2)求直线与平面所成角的正弦值．
63．（2024·江苏·三模）如图，三棱锥P－ABC的底面为等腰直角三角形，∠ABC＝90°，AB＝2．D，E分别为AC，BC的中点，PD⊥平面ABC，点M在线段PE上．
(1)再从条件①、②、③、④四个条件中选择两个作为已知，使得平面MBD⊥平面PBC，并给予证明；
(2)在（1）的条件下，求直线BP与平面MBD所成的角的正弦值．
条件①：；
条件②：∠PED＝60°；
条件③：PM＝3ME：
条件④：PE＝3ME．
名称
定义
空间向量
在空间中，具有大小和方向的量
相等向量
方向相同且模相等的向量
相反向量
长度相等而方向相反的向量
共线向量(或平行向量)
表示若干空间向量的有向线段所在的直线互相平行或重合的向量
共面向量
平行于同一个平面的向量
向量表示
坐标表示
数量积
a·b
a1b1＋a2b2＋a3b3
共线
a＝λb(b≠0，λ∈R)
a1＝λb1，a2＝λb2，a3＝λb3
垂直
a·b＝0(a≠0，b≠0)
a1b1＋a2b2＋a3b3＝0
模
|a|
eq \r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3))
夹角余弦值
cs〈a，b〉＝eq \f(a·b,|a||b|)(a≠0，b≠0)
cs〈a，b〉＝eq \f(a1b1＋a2b2＋a3b3,\r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3))·\r(b\\al(2,1)＋b\\al(2,2)＋b\\al(2,3)))
位置关系
向量表示
直线l1，l2的方向向量分别为n1，n2
l1∥l2
n1∥n2⇔n1＝λn2(λ∈R)
l1⊥l2
n1⊥n2⇔n1·n2＝0
直线l的方向向量为n，平面α的法向量为m，l⊄α
l∥α
n⊥m⇔n·m＝0
l⊥α
n∥m⇔n＝λm(λ∈R)
平面α，β的法向量分别为n，m
α∥β
n∥m⇔n＝λm(λ∈R)
α⊥β
n⊥m⇔n·m＝0
（一）
用已知向量表示某一向量的三个关键点
(1)要结合图形，以图形为指导是解题的关键．
(2)要正确理解向量加法、减法与数乘运算的几何意义．
(3)在立体几何中，三角形法则、平行四边形法则仍然成立．
题型1：空间向量的线性运算
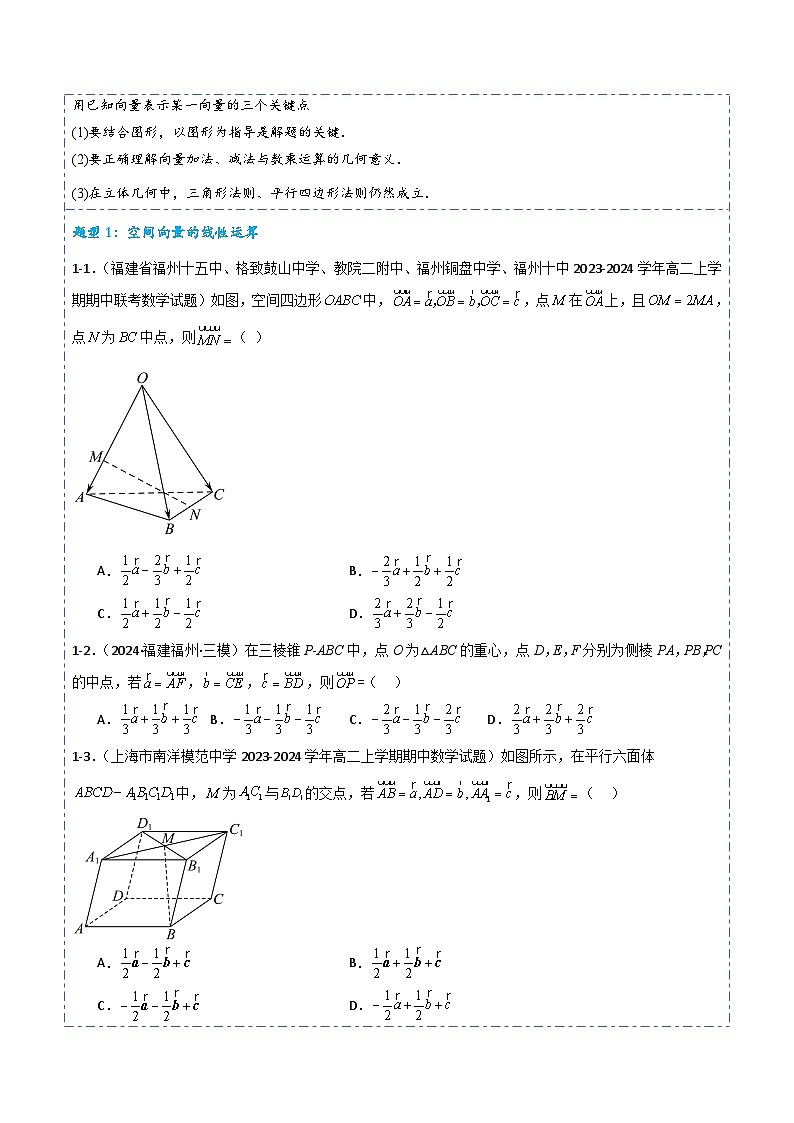
1-1．（福建省福州十五中、格致鼓山中学、教院二附中、福州铜盘中学、福州十中2023-2024学年高二上学期期中联考数学试题）如图，空间四边形中，，点在上，且，点为中点，则（ ）
A．B．
C．D．
1-2．（2024·福建福州·三模）在三棱锥P-ABC中，点O为△ABC的重心，点D，E，F分别为侧棱PA，PB，PC的中点，若，，，则=（ ）
A．B．C．D．
1-3．（上海市南洋模范中学2023-2024学年高二上学期期中数学试题）如图所示，在平行六面体中，为与的交点，若，则（ ）

A．B．
C．D．
1-4．（2024高二上·陕西西安·期末）如图，在四面体中，是的重心，是上的一点，且，若，则为（ ）
A．B．
C．D．
（二）
应用共线(面)向量定理、证明点共线(面)的方法比较
三点(P，A，B)共线
空间四点(M，P，A，B)共面
eq \(PA,\s\up6(→))＝λeq \(PB,\s\up6(→))
eq \(MP,\s\up6(→))＝xeq \(MA,\s\up6(→))＋yeq \(MB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋teq \(AB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝eq \(OM,\s\up6(→))＋xeq \(MA,\s\up6(→))＋yeq \(MB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝xeq \(OA,\s\up6(→))＋(1－x)eq \(OB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝xeq \(OM,\s\up6(→))＋yeq \(OA,\s\up6(→))＋(1－x－y)eq \(OB,\s\up6(→))
题型2：空间向量基本定理及其应用
2-1．（2024高二上·湖南郴州·阶段练习）已知，，如果与为共线向量，则（ ）
A．B．C．D．
2-2．（2024高二·全国·课后作业）若、、三点共线，则（ ）．
A．
B．
C．
D．
2-3．（湖南省岳阳市平江县2023-2024学年高二上学期1月期末数学试题）已知A、B、C三点不共线，对平面外的任一点O，下列条件中能确定点M与点A、B、C一定共面的是（ ）
A．B．
C．D．
2-4．（2024高二下·四川雅安·期末）向量，分别是直线，的方向向量，且，，若，则（ ）
A．，B．，
C．，D．，
2-5．（2024高二下·江苏扬州·期中）已知空间、、、四点共面，且其中任意三点均不共线，设为空间中任意一点，若，则（ ）
A．B．C．D．
2-6．（2024高二上·湖南郴州·阶段练习）为空间任意一点，若，若、、、四点共面，则（ ）
A．B．C．D．
2-7．（2024高三·全国·专题练习）已知，若三向量共面，则等于（ ）
A．B．9C．D．
2-8．（2024高二·全国·课后作业）在四面体OABC中，点M，N分别为OA、BC的中点，若，且G、M、N三点共线，则 ．
（三）
空间向量数量积及其应用
空间向量的数量积运算有两条途径，一是根据数量积的定义，利用模与夹角直接计算；二是利用坐标运算．
题型3：空间向量数量积及其应用
3-1．【多选】（2024高二上·辽宁大连·期末）已知向量，，则下列正确的是（ ）
A．B．C．D．
3-2．（2024高二上·山东济宁·阶段练习）已知是棱长为2的正方体内切球的一条直径，则 ．
3-3．（2024·上海松江·二模）已知空间向量，，，若，则 ．
3-4．（2024高二上·重庆万州·阶段练习）已知空间向量，，则在方向上的投影向量为 .
3-5．（2024·黑龙江哈尔滨·模拟预测）如图，平行六面体中，，，，，则线段的长为 .

3-6．【多选】（2024高三上·黑龙江哈尔滨·期中）如图，在平行六面体中，其中以顶点A为端点的三条棱长均为6，且彼此夹角都是，下列说法中不正确的是（ ）

A．
B．
C．向量与夹角是
D．向量与所成角的余弦值为
3-7．【多选】（2024高二上·浙江温州·期末）已知空间向量，，下列说法正确的是（ ）
A．若，则
B．若，则
C．若在上的投影向量为，则
D．若与夹角为锐角，则
3-8．【多选】（2024·安徽·一模）在平行六面体中，已知，，则（ ）
A．直线与所成的角为
B．线段的长度为
C．直线与所成的角为
D．直线与平面所成角的正弦值为
（四）
向量法证明平行、垂直
(1)利用向量法证明平行、垂直关系，关键是建立恰当的坐标系(尽可能利用垂直条件，准确写出相关点的坐标，进而用向量表示涉及到直线、平面的要素)．
(2)向量证明的核心是利用向量的数量积或数乘向量，但向量证明仍然离不开立体几何的有关定理．
题型4：向量法证明平行
4-1．（2024高三·全国·专题练习）四棱锥中，底面为矩形，平面，为的中点，证明：平面.
4-2．（2024高二下·江苏·课后作业）如图所示，平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，且PA＝AD＝2，E，F，G分别是线段PA，PD，CD的中点，求证：平面EFG∥平面PBC．
4-3．（2024高二·全国·课后作业）如图，在直四棱柱中，底面为等腰梯形，，，，，是棱的中点．求证：平面平面.
4-4．（2024高二·全国·专题练习）如图，在四棱锥中，底面为矩形，平面平面，，，，，分别是，的中点. 求证：平面.

4-5．（2024高二上·全国·课后作业）如图所示，在四棱锥中，底面为矩形，平面，为的中点，为的中点，，求证：．

题型5：向量法证明垂直
5-1．（2024高三·全国·专题练习）如图，在四棱锥中，平面，，，，.为的中点，点在上，且.
求证：平面平面.
5-2．（2024高二·全国·专题练习）已知在直三棱柱中，其中为的中点，点是上靠近的四等分点，与底面所成角的余弦值为．

求证：平面平面.
5-3．（2024高三·全国·专题练习）如图，已知直三棱柱为的中点，为侧棱上一点，且，三棱柱的体积为32．过点作，垂足为点，求证：平面；
5-4．（2024高三·全国·专题练习）如图，在四棱锥中，底面，底面是边长为2的正方形，，，分别是，的中点．求证：平面；
5-5．（2024高二上·山西太原·期中）如图，在平行六面体中，.
(1)求的长；
(2)求证：.