备战2025年高考数学精品课件第九章 第2讲 用样本估计总体

这是一份备战2025年高考数学精品课件第九章 第2讲 用样本估计总体，共60页。PPT课件主要包含了平均数，方差和标准差，常用结论，平均数的性质，方差的性质，ABD，ABC，ACD等内容，欢迎下载使用。
学生用书P2121. 百分位数(1)定义：一般地，一组数据的第 p 百分位数是这样一个值，它使得这组数据中至少 有① 的数据小于或等于这个值，且至少有② ⁠的数据大于或 等于这个值.(2)四分位数：第25百分位数、中位数(第50百分位数)、第75百分位数把一组由 小到大排列后的数据分成四等份，这三个分位数统称为四分位数.其中第25百 分位数也称为第一四分位数或下四分位数等，第75百分位数也称为第三四分位 数或上四分位数等.
(100－ p )％　
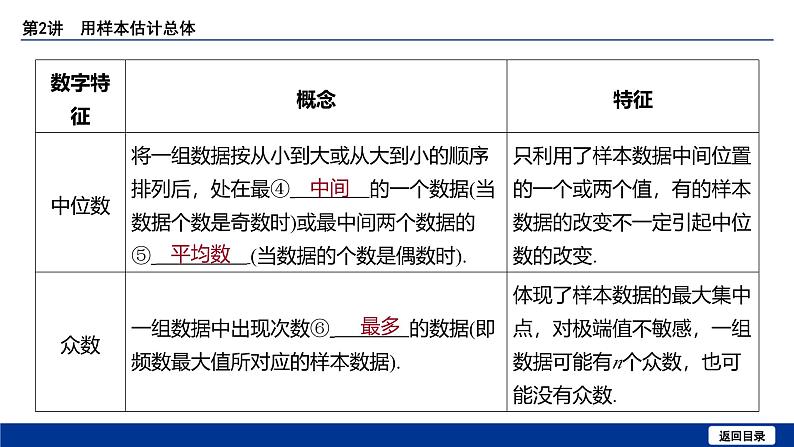
2. 平均数、中位数、众数
4. 分层随机抽样的样本均值与方差
若给定一组数据 x 1， x 2，…， xn ，其方差为 s 2，则 ax 1， ax 2，…， axn 的方差为 a 2 s 2， ax 1＋ b ， ax 2＋ b ，…， axn ＋ b 的方差为 a 2 s 2.
特别地，当 a ＝1时，有 x 1＋ b ， x 2＋ b ，…， xn ＋ b 的方差为 s 2，这说明将一组数 据中的每一个数据都加上一个相同的常数，方差是不变的，即数据经过平移后方差 不变.
1. 下列说法正确的是(　D　)
[解析]　平均数指的是这组数据的平均水平，中位数指的是这组数据的中间水平， 它们之间没有必然联系，故A错误；一组数据的第 p 百分位数可以不唯一，故B错 误；方差是标准差的平方，故它们的单位不一样，故C错误.
2. [全国卷Ⅲ]设一组样本数据 x 1， x 2，…， xn 的方差为0.01，则数据10 x 1，10 x2，…，10 xn 的方差为(　C　)
[解析]　因为数据 axi ＋ b ( i ＝1，2，…， n )的方差是数据 xi ( i ＝1，2，…， n )的方 差的 a 2倍，所以所求数据的方差为102×0.01＝1.
3. [多选/2021新高考卷Ⅱ]下列统计量中可用于度量样本 x 1， x 2，…， xn 离散程度的 有(　AC　)
[解析]　平均数、众数和中位数均刻画了样本数据的集中趋势，一般地，对数值型 数据集中趋势的描述，可以用平均数和中位数，对分类型数据集中趋势的描述，可 以用众数.方差、标准差和极差均是度量样本数据离散程度的数字特征.故选AC.
4. [江苏高考]已知一组数据6，7，8，8，9，10，则该组数据的方差是 ⁠.
5. [2023湖南省六校联考]数据：1，2，2，3，4，5，6，6，7，8，其中位数为 m ， 第60百分位数为 a ，则 m ＋ a ＝ ⁠.
学生用书P213命题点1　百分位数的估计例1 (1)一个容量为20的样本，其数据按从小到大的顺序排列为：1，2，2，3，5， 6，6，7，8，8，9，10，13，13，14，15，17，17，18，18.则该组数据的第75百分 位数为 ，第86百分位数为 ⁠.
(2)[2023重庆二调]如图是根据某班学生在一次体能素质测试中的成绩画出的频率分 布直方图，则由直方图得到的80％分位数为 ⁠.
解得 x ＝78.5.
方法技巧1. 计算一组 n 个数据的第 p 百分位数的步骤(1)按从小到大排列原始数据；(2)计算 i ＝ n × p ％；(3)若 i 不是整数，而大于 i 的比 邻整数为 j ，则第 p 百分位数为第 j 项数据；若 i 是整数，则第 p 百分位数为第 i 项与 第( i ＋1)项数据的平均数.
2. 频率分布直方图中第 p 百分位数的求解步骤
(1)确定第 p 百分位数所在的区间[ a ， b )；
训练1 (1)已知100个数据的第75百分位数是9.3，则下列说法正确的是(　C　)
[解析]　因为100×75％＝75，为整数，所以第75个数据和第76个数据的平均数为第 75百分位数，是9.3，则C正确，其他选项均不正确，故选C.
(2)[2023河北名校联考]为科普航天知识，某校组织学生参与航天知识竞答活动，某 班8位同学成绩如下：7，6，8，9，8，7，10， m .若去掉 m ，该组数据的第25百分 位数保持不变，则整数 m (1≤ m ≤10)的值可以是 .(写出一个满 足条件的 m 的值即可)
[解析]　原数据去掉 m 后，剩余数据从小到大依次为6，7，7，8，8，9，10，因为 7×0.25＝1.75，所以这7个数的第25百分位数为7，所以数据7，6，8，9，8，7， 10， m 的第25百分位数为7，又8×0.25＝2，所以7为这8个数据从小到大排序后的第 2个数与第3个数的平均数，所以 m (1≤ m ≤10)的值可以是7或8或9或10.
7(8，9，10也可)　
(2)[多选/2023新高考卷Ⅰ]有一组样本数据 x 1， x 2，…， x 6，其中 x 1是最小值， x 6是 最大值，则(　BD　)
角度2　统计图中的数字特征例3 [多选/2023重庆市三检]某学校共有2 000名男生，为了了解这部分学生的身体发 育情况，学校抽查了100名男生的体重情况.根据所得数据绘制样本的频率分布直方 图如图所示，则下列结论正确的是(　ABD　)
方法技巧频率分布直方图中的数字特征(1)众数：在频率分布直方图中，一般用最高小长方形的底边中点的横坐标近似 代替；(2)中位数：在频率分布直方图中，中位数左边和右边的直方图的面积应该相等；(3)平均数：平均数在频率分布直方图中近似等于各组区间的中点值与对应频率之积 的和.
训练2 (1)[2022全国卷甲]某社区通过公益讲座以普及社区居民的垃圾分类知识.为了 解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分 类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如图，则(　B　)
(2)[多选/2021新高考卷Ⅰ]有一组样本数据 x 1， x 2，…， xn ，由这组数据得到新样本 数据 y 1， y 2，…， yn ，其中 yi ＝ xi ＋ c ( i ＝1，2，…， n )， c 为非零常数，则 (　CD　)
命题点3　总体数字特征的估计角度1　总体集中趋势的估计例4 统计局就某地居民的月收入(单位：元)情况调查了10 000人，并根据所得数据画 出了样本频率分布直方图(如图)，每个分组包括左端点，不包括右端点，如第一组 表示月收入在[2 500，3 000)内.
(1)为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这10 000人 中用分层随机抽样的方法抽出100人进行下一步分析，则月收入在[4 000，4 500)内 的应抽取多少人？
(3)样本平均数为(2 750×0.000 2＋3 250×0.000 4＋3 750×0.000 5＋4 250×0.000 5＋4 750×0.000 3＋5 250×0.000 1)×500＝3 900，因此估计该地居民月收入的平均数为3 900元.
(3)假设同组中的数据用该组区间的中点值代替，估计该地居民月收入的平均数.
(2)估计该地居民的月收入的中位数.
方法技巧平均数、中位数和众数等都是刻画“中心位置”的量，它们从不同角度刻画了一组 数据的集中趋势.一般地，对数值型数据(如用水量、身高、收入、产量等)集中趋势 的描述，可以用平均数、中位数；而对分类型数据(如校服规格、性别、产品质量等 级等)集中趋势的描述，可以用众数.
角度2　总体离散程度的估计
例5 [2023全国卷乙]某厂为比较甲、乙两种工艺对橡胶产品伸缩率的处理效 应，进行10次配对试验，每次配对试验选用材质相同的两个橡胶产品，随机地 选其中一个用甲工艺处理，另一个用乙工艺处理，测量处理后的橡胶产品的伸 缩率，甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为 xi ， yi ( i ＝1， 2，…，10)，试验结果如下：
[解析]　(1)由题意，求出 zi 的值如表所示，
方法技巧总体离散程度的估计标准差(方差)刻画了数据的离散程度或波动幅度，标准差(方差)越大，数据的离散程 度越大，越不稳定；标准差(方差)越小，数据的离散程度越小，越稳定.
训练3 [全国卷Ⅱ]某行业主管部门为了解本行业中小企业的生产情况，随机调查 了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率 y 的 频数分布表.
(1)分别估计这类企业中产值增长率不低于40％的企业比例、产值负增长的企 业比例；
命题点4　分层随机抽样的均值与方差例6 某校开展了为期一年的“弘扬传统文化，阅读经典名著”活动.在了解全校学生 每年平均阅读了多少本文学经典名著时，甲同学抽取了一个容量为10的样本，并算 得样本的平均数为5，方差为9；乙同学抽取了一个容量为8的样本，并算得样本的 平均数为6，方差为16.已知甲、乙两同学抽取的样本合在一起组成一个容量为18的 样本，则合在一起后的样本平均数为 ，方差为 .(精确到0.1)
训练4 [2023安徽省示范高中联考]为了调查公司员工的健康状况，某公司男、女员工 比例是2∶3，用分层随机抽样的方法抽取样本，统计样本数据如下：男员工的平均 体重为70 kg，标准差为5 kg；女员工的平均体重为50 kg，标准差为 6 kg.则由此估 计该公司员工的平均体重是 kg，方差是 kg2.
3. [命题点2，4/2023潍坊市高三统考]若一组样本数据 x 1， x 2，…， xn 的平均数为 10，另一组样本数据2 x 1＋4，2 x 2＋4，…，2 xn ＋4的方差为8，则两组样本数据合 并为一组样本数据后的平均数和方差分别为(　A　)
4. [命题点3/2021全国卷乙]某厂研制了一种生产高精产品的设备，为检验新设备生产 产品的某项指标有无提高，用一台旧设备和一台新设备各生产了10件产品，得到各 件产品该项指标数据如下：
5. [命题点4/2023广州市调研]为调查某地区中学生每天的睡眠时间，采用样本量比例 分配的分层随机抽样，现抽取初中生800人，其每天睡眠时间均值为9小时，方差为 1，抽取高中生1 200人，其每天睡眠时间均值为8小时，方差为0.5，则估计该地区 中学生每天睡眠时间的方差为(　B　)
学生用书·作业帮P375
1. [2024福州市一检]某市抽查一周空气质量指数变化情况，得到一组数据：80， 76，73，82，86，75，81.以下关于这组数据判断正确的有(　C　)
[解析]　对A，B，将这组数据按从小到大的顺序排列为73，75，76，80， 81，82，86，则这组数据的极差为86－73＝13，这组数据的中位数为80，A错 误，B错误；对C，(80＋76＋73＋82＋86＋75＋81)÷7＝79，C正确；对D， [(80－79)2＋(76－79)2＋(73－79)2＋(82－79)2＋(86－79)2＋(75－79)2＋(81－ 79)2]÷7≈17.7，D错误.故选C.
2. [2024湖北部分学校联考]为了弘扬体育精神，某学校组织秋季运动会，在一项比 赛中，学生甲进行了8组投篮，得分分别为10，8， a ，8，7，9，6，8，如果学生甲 的平均得分为8分，那么这组数据的第75百分位数为(　C　)
3. [全国卷Ⅱ]演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩 时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分 与9个原始评分相比，不变的数字特征是(　A　)
[解析]　记9个原始评分分别为 a ， b ， c ， d ， e ， f ， g ， h ， i (按从小到大的顺序 排列)，易知 e 为7个有效评分与9个原始评分的中位数，故不变的数字特征是中位 数，故选A.
4. [2024河南名校联考]在某次考试中，某班学生的最高分为100分，最低分为50分， 且最高分只有1个，现将全班每个学生的分数按照 yi ＝ axi ＋ b ( a ＞0)进行调整，其 中 xi 是第 i 个学生的原始分数， yi 是第 i 个学生调整后的分数，若调整后，全班的最 高分为100分，最低分为60分，则(　B　)
[解析]　对于A，B：根据题意知100＝100 a ＋ b ，60＝50 a ＋ b ，所以 a ＝0.8， b ＝ 20，于是 yi ＝0.8 xi ＋20，则 yi － xi ＝0.8 xi ＋20－ xi ＝20－0.2 xi ＝0.2(100－ xi )≥0， 即除了最高分外，调整后的分数都高于原始分数，因此调整后分数的平均数、中位 数分别高于原始分数的平均数、中位数，A错误，B正确.
对于C：根据 yi ＝0.8 xi ＋20，可得调整后分数的标准差等于原始分数的标准差的0.8 倍，显然调整后分数的标准差变小了，故C错误.
对于D：如果原始分数相同，则调整后的分数也相同，故调整后分数的众数个数和 原始分数的众数个数相同，故D错误.
5. [多选/2024云南昆明模拟]甲、乙两个旅游景区某月初连续7天的日均气温(单位： ℃)数据如图所示(气温均取整数)，则关于这7天的日均气温，下列判断正确的是 (　ABC　)
6. [多选/2023合肥市二检]如图是某汽车公司100家销售商2022年新能源汽车销售量 (单位：辆)的频率分布直方图，则(　ACD　)
[解析]　对于A，由频率分布直方图可得，50×0.002＋50×0.003＋50 a ＋50×0.006 ＋50 a ＋50×0.001＝1，得 a ＝0.004，故A正确；对于B，(25×0.002＋75×0.003＋ 125×0.004＋175×0.006＋225×0.004＋275×0.001)×50＝150，故B错误；对于C， 设80％分位数为 x ，易得 x ∈[200，250)，则50×0.002＋50×0.003＋50×0.004＋ 50×0.006＋( x －200)×0.004＝0.8，解得 x ＝212.5，故C正确；对于D，销售量在 [200，300]内的频率为50×0.004＋50×0.001＝0.25，20×0.25＝5，所以从销售量在 [200，300]内的销售商中抽取5家，故D正确.故选ACD.
8. [2024新疆喀什模拟]样本中共有五个个体，其值分别为 a ，0，1，2，3，若该样 本的平均值为1，则样本方差为 ⁠.
9. [2024陕西商洛联考]某品牌汽车2019—2022年这四年的销量逐年增长，2019年销 量为5万辆，2022年销量为22万辆，且这四年销量的中位数与平均数相等，则这四 年的总销量为 万辆.
11. [2023广西联考]某新能源汽车制造公司，为鼓励消费者购买其生产的新能源汽 车，约定从2023年1月开始，凡购买一辆该品牌汽车，在行驶三年后，公司将给予 适当金额的购车补贴.某调研机构对已购买该品牌汽车的消费者，就购车补贴金额的 心理预期值进行了抽样调查，得其样本频率分布直方图如图所示.
(1)求实数 m 的值；(2)估计已购买该品牌汽车的消费群体对购车补贴金额的心理预期值的平均数(同一 组数据用该区间的中点值作代表)和中位数；(精确到0.01)
[解析]　(1)由题意知，1×(0.10＋0.30＋0.30＋ m ＋0.10＋0.05)＝1，解得 m ＝0.15.
(3)现在要从购车补贴金额的心理预期值在区间[3，5)的样本中用分层随机抽样的方 法抽取6人，再从这6人中随机抽取2人进行调查，求抽到的2人购车补贴金额的心理 预期值都在区间[3，4)的概率.
13. 某学校统计教师职称及年龄，中级职称教师的人数为50，其平均年龄为38岁， 方差是2，高级职称的教师中有3人58岁，5人40岁，2人38岁，则该校中级职称和高 级职称教师年龄的平均数和方差分别为 和 .(平均数精确到0.1)
14. 某“双一流A类”大学就业部从该校2023年已就业的大学本科毕业生中随机抽取 了100人进行问卷调查，其中一项是他们的月薪收入情况，调查发现，他们的月薪 收入在1.65万元到2.35万元之间，根据统计数据分组，得到如下的频率分布直方 图，同一组数据用该区间的中点值作代表.
方案二：这50人共收取费用约为50×0.03×2＝3(万元).故方案一能收到更多的费用.
15. [设问创新/2024重庆统考]四名同学各掷骰子5次，分别记录每次骰子出现的点 数，根据四名同学的统计结果，可以判断出一定没有出现点数6的是(　A　)