备战2025年高考数学精品课件第八章 第8讲 直线与圆锥曲线的位置关系

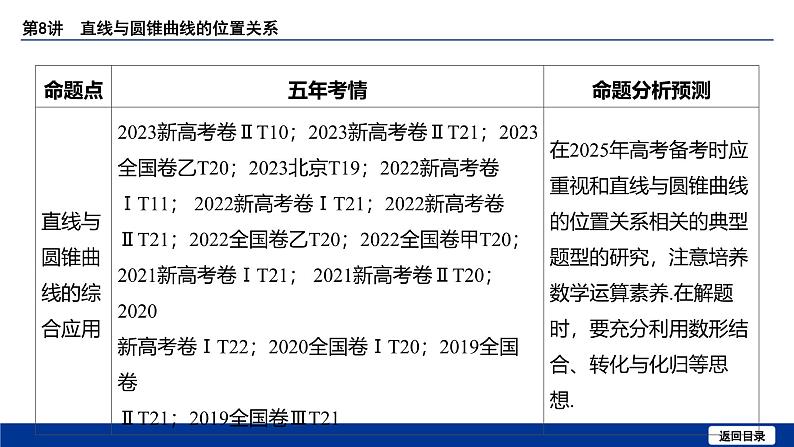
这是一份备战2025年高考数学精品课件第八章 第8讲 直线与圆锥曲线的位置关系，共60页。PPT课件主要包含了Δ＞0，Δ＜0，弦长与中点弦，1弦长公式，2中点弦，答案不唯一，角度1弦长问题，角度2中点弦问题，方法技巧，ABD等内容，欢迎下载使用。
1. 直线与圆锥曲线位置关系的判断将直线方程与圆锥曲线的方程联立，消去 y (或 x )，得到关于 x (或 y )的一元二次方 程，设其判别式为Δ，则① ⇔有两个交点 ⇔相交；Δ＝0⇔有一个交点⇔相 切；② ⇔无交点⇔相离.注意　 直线与双曲线方程联立消元后，得出的方程中二次项系数为零时，直线与双 曲线渐近线平行，两者有且只有一个交点；二次项系数不为零时，利用判别式进行 判断.
3. 切线与切点弦所在直线的方程
3. 已知直线 l ： y ＝ x －1与抛物线 y 2＝4 x 交于 A ， B 两点，则线段 AB 的长是 (　C　)
方法技巧(1)直线与椭圆的位置关系问题可直接转化为直线与椭圆的交点个数问题.(2)直线与双曲线只有一个交点，则直线与双曲线相切或直线与双曲线的渐近线平行.(3)直线与抛物线只有一个交点，则直线与抛物线相切或直线与抛物线的对称轴平行 (或重合).(4)对于过定点的直线，可以根据定点与圆锥曲线的位置关系判断直线与圆锥曲线的 位置关系，注意数形结合的应用.
训练1 (1)[2023天津高考]过原点 O 的一条直线与圆 C ：( x ＋2)2＋ y 2＝3相切，交曲线 y 2＝2 px ( p ＞0)于点 P ，若｜ OP ｜＝8，则 p 的值为 ⁠.
命题点2　弦长及中点弦问题
例3 [2023成都市模拟]已知抛物线 C ： y 2＝2 px ( p ＞0， p ≠4)，过点 A (2，0)且斜率 为 k 的直线与抛物线 C 相交于 P ， Q 两点.
(1)设点 B 在 x 轴上，分别记直线 PB ， QB 的斜率为 k 1， k 2，若 k 1＋ k 2＝0，求点 B 的坐标；
方法技巧(1)使用弦长公式时注意对直线斜率的讨论.(2)直线经过特殊点(如焦点、原点等)或斜率特殊时，利用圆锥曲线的定义或数形结 合来求弦长.
点差法解决中点弦问题的步骤
(1)设弦的两个端点： A ( x 1， y 1)， B ( x 2， y 2)；
(2)将两点坐标分别代入圆锥曲线方程中并两式作差，得到关于直线 AB 的斜率和线 段 AB 的中点坐标的关系式；
(3)将已知条件代入关系式并化简求解.
训练2 (1)已知 F 为抛物线 C ： y 2＝4 x 的焦点，过 F 作两条互相垂直的直线 l 1， l 2， 直线 l 1与 C 交于 A ， B 两点，直线 l 2与 C 交于 D ， E 两点，则｜ AB ｜＋｜ DE ｜的 最小值为(　A　)
方法技巧(1)曲线的切线方程可以利用判别式求解，也可以利用导数的几何意义求解.(2)“代一半，留一半”是曲线的切线方程与切点弦所在直线方程相关结论的记 忆口诀.
训练3 [2023山西运城模拟]过点 P 作抛物线 C ： x 2＝4 y 的切线 l 1， l 2，切点分别为 M ， N ，若△ PMN 的重心坐标为(3，4)，则 P 点坐标为(　A　)
(2)设 P 为第一象限内 E 上的动点，直线 PD 与直线 BC 交于点 M ，直线 PA 与直线 y ＝－2交于点 N ，求证： MN ∥ CD .
方法技巧(1)解答直线与圆锥曲线相交的题目时，常用到“设而不求”的方法，即联立直线和 圆锥曲线的方程，消去 y (或 x )得一元二次方程，然后借助根与系数的关系，并结合 题设条件，建立有关参变量的等量关系求解；(2)涉及直线方程的设法时，务必考虑全面，不要忽略直线斜率为0或不存在等特殊 情形.
(1)求 C 的方程；
解法二　由“蒙日圆”定理可得，点 P 的轨迹方程为 C 1： x 2＋ y 2＝4，所以要使圆 C 2：( x －3)2＋( y －4)2＝ r 2( r ＞0)上总存在点 P 满足题意，则圆 C 1与 C 2有交点，所 以｜2－ r ｜≤｜ C 1 C 2｜≤2＋ r ，又｜ C 1 C 2｜＝5，所以3≤ r ≤7，故选B.
性质1： PA ⊥ PB .
性质2：(1) C ， O ， D 三点共线；
(2) CD ∥ AB ；
性质3： PO 平分椭圆的切点弦 AB .
4. [命题点3/多选/2023重庆市调研质量抽测]设 O 为坐标原点， F 为抛物线 C ： x 2＝2 py ( p ＞0)的焦点，过焦点 F 且倾斜角为θ的直线 l 与抛物线 C 交于 M ， N 两点(点 M 在第二象限)，当θ＝30°时，｜ MF ｜＝2，则下列说法正确的是(　ABD　)
(1)求椭圆的方程和离心率 e ；
(2)已知点 P 是椭圆上一动点(不与端点重合)，直线 A 2 P 交 y 轴于点 Q ，若三角形 A 1 PQ 的面积是三角形 A 2 FP 的面积的二倍，求直线 A 2 P 的方程.
3. [2024南昌市模拟]已知抛物线 C ： x 2＝4 y 的焦点为 F ， P 是抛物线 C 在第一象限 内的一点，过点 P 作 C 的准线的垂线，垂足为 M ， FM 的中点为 N ，若直线 PN 经过 点(0，－3)，则直线 PN 的斜率为(　C　)
4. [多选/2024牡丹江月考]已知直线 l ： x ＝ ty ＋2与抛物线 C ： y 2＝8 x 交于 A ， B 两 点，若线段 AB 的中点是 M ( m ，2)，则(　AB　)
(1)求椭圆 C 的标准方程；
(2)若 b ＝1，过点 F 作与直线 AB 平行的直线 l ， l 与 C 交于 P ， Q 两点，求直线 OP 的斜率与直线 OQ 的斜率的乘积.
10. [多选]在平面直角坐标系 xOy 中，点 A (－1，0)在抛物线 C ： y 2＝2 px ( p ＞0)的 准线上，过抛物线 C 的焦点 F 作直线 l 交 C 于 P ， Q 两点，点 B (2，0)，则下列结论 正确的是(　BCD　)
[解析]　由题可知，抛物线 C 的准线方程为 x ＝－1，所以 p ＝2，则 F (1，0)，抛物 线 C ： y 2＝4 x .设 P ( x 1， y 1)， Q ( x 2， y 2)，直线 l 的方程为 x ＝ ty ＋1，(巧设直线方 程，可避免分类讨论，也可以将直线方程设为 y ＝ k ( x －1)，但此时要记得讨论直线 斜率不存在的情况)代入抛物线 C 的方程，消去 x 得 y 2－4 ty －4＝0，所以 y 1＋ y 2＝4 t ， y 1 y 2＝－4.
12. [2024青岛市检测]已知 O 为坐标原点， A (1，0)， B (－1，0)，直线 AM ， BM 的 斜率之积为4，记动点 M 的轨迹为 E . (1)求 E 的方程；
(2)过点 P (－2，1)作斜率为 k 的直线与椭圆 E 交于不同的两点 B ， C ，直线 AB ， AC 分别与 x 轴交于点 M ， N . 当｜ MN ｜＝2时，求 k 的值.