备战2025年高考数学精品课件第六章 第4讲 余弦定理、正弦定理

这是一份备战2025年高考数学精品课件第六章 第4讲 余弦定理、正弦定理，共60页。PPT课件主要包含了RsinB，RsinC，内切圆，等边三角形，ABD，钝角三角形等内容，欢迎下载使用。
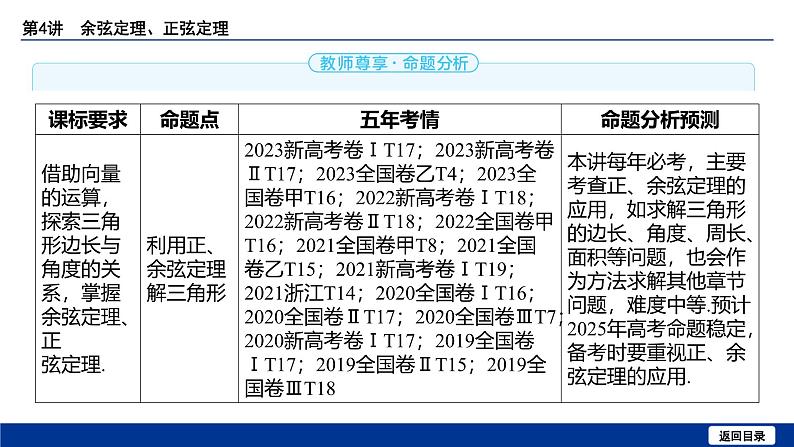
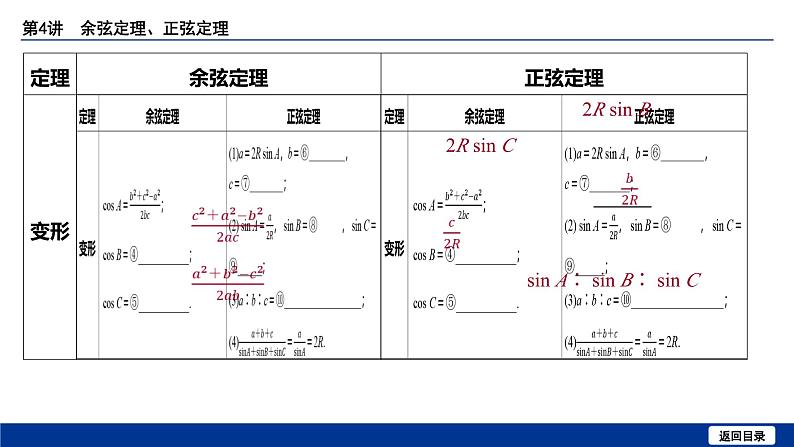
1. 余弦定理、正弦定理 在△ ABC 中，若角 A ， B ， C 所对的边分别是 a ， b ， c ， R 为△ ABC 的外接圆半 径，则
c2＋a2－2ca cs B　
a2＋b2－2ab cs C　
2R sin C
sin A∶ sin B∶ sin C　
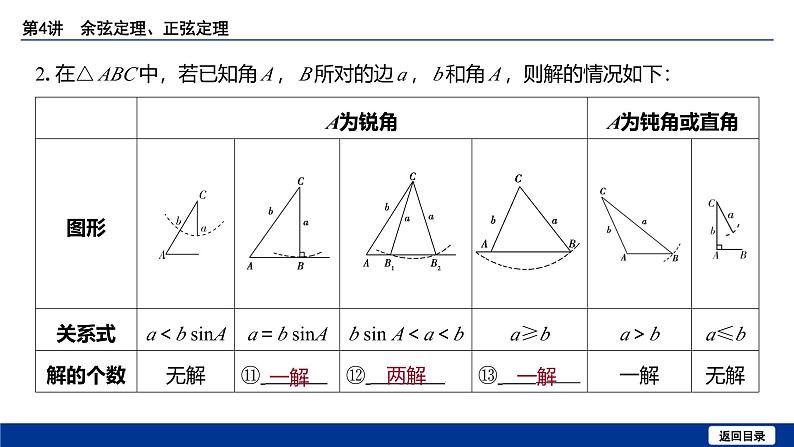
2. 在△ ABC 中，若已知角 A ， B 所对的边 a ， b 和角 A ，则解的情况如下：
1. 以下说法正确的是(　A　)
[解析]　由余弦定理得 AC 2＝ AB 2＋ BC 2－2 AB · BC · cs B ，得 BC 2＋2 BC －15＝ 0，解得 BC ＝3或 BC ＝－5(舍去).故选D.
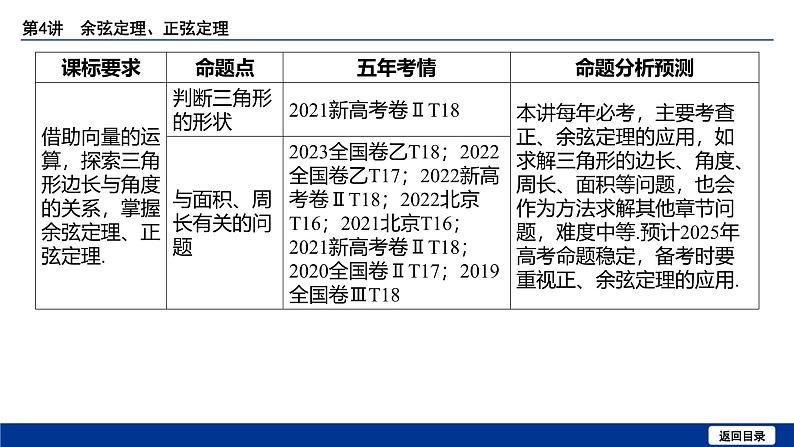
3. [多选]记△ ABC 的内角 A ， B ， C 的对边分别为 a ， b ， c ，则符合下列条件的△ ABC 有且只有一个的是(　AC　)
4. 已知2 a ＋1， a ，2 a －1是钝角三角形的三边， 则实数 a 的取值范围是 ⁠.
方法技巧判断三角形形状的方法(1)化为边：通过正、余弦定理将角化边，利用因式分解、配方等得出边之间的关系 进行判断.判断技巧：
(2)化为角：通过正、余弦定理将边化角，通过三角恒等变换公式、三角形的内角和 定理得出角的大小或角之间的关系.注意　(1)不能随意约掉公因式，要移项、提取公因式，否则会有遗漏一种形状的可 能.(2)注意挖掘隐含条件，在变形过程中注意角的范围对三角函数值的影响.
训练2 [2021新高考卷Ⅱ]在△ ABC 中，角 A ， B ， C 所对的边分别为 a ， b ， c ， b ＝ a ＋1， c ＝ a ＋2.(1)若2 sin C ＝3 sin A ，求△ ABC 的面积.
(2)是否存在正整数 a ，使得△ ABC 为钝角三角形？若存在，求 a ；若不存在，说明 理由.
命题点3　与面积、周长有关的问题角度1　面积问题例3 [2023全国卷乙]在△ ABC 中，已知∠ BAC ＝120°， AB ＝2， AC ＝1.(1)求 sin ∠ ABC ；
(2)若 D 为 BC 上一点，且∠ BAD ＝90°，求△ ADC 的面积.
角度2　周长问题例4 [2022全国卷乙]记△ ABC 的内角 A ， B ， C 的对边分别为 a ， b ， c ， 已知 sin C sin ( A － B )＝ sin B sin ( C － A ).(1)证明：2 a 2＝ b 2＋ c 2；
解法二　因为 A ＋ B ＋ C ＝π，所以 sin C sin ( A － B )＝ sin ( A ＋ B ) sin ( A － B )＝ sin 2 A cs 2 B － cs 2 A sin 2 B ＝ sin 2 A (1－ sin 2 B )－(1－ sin 2 A ) sin 2 B ＝ sin 2 A － sin 2 B . 同理有 sin B sin ( C － A )＝ sin ( C ＋ A ) sin ( C － A )＝ sin 2 C － sin 2 A ，所以 sin 2 A － sin 2 B ＝ sin 2 C － sin 2 A ，由正弦定理可得2 a 2＝ b 2＋ c 2.
(2)由(1)及 a 2＝ b 2＋ c 2－2 bc cs A 得， a 2＝2 bc cs A ，所以2 bc ＝31.因为 b 2＋ c 2＝2 a 2＝50，所以( b ＋ c )2＝ b 2＋ c 2＋2 bc ＝81，得 b ＋ c ＝9，所以△ ABC 的周长为 a ＋ b ＋ c ＝14.
方法技巧与周长有关问题的解题思路(1)若边长易求，直接求出边长，进而求出周长；(2)若边长不易求，可利用整体思想，构造以两边长的和为未知数的方程求解，进而 求出周长.
方法技巧射影定理：在△ ABC 中， a ， b ， c 分别为内角 A ， B ， C 的对边，则 a ＝ b cs C ＋ c cs B ， b ＝ a cs C ＋ c cs A ， c ＝ a cs B ＋ b cs A .
3. [命题点1/2024杭州市质检]已知四边形 ABCD 是一个圆的内接四边形，如图，若 AB ＝1， BC ＝3， CD ＝ DA ＝2.(1)求线段 BD 的长；
[解析]　由余弦定理得 b 2＝ a 2＋ c 2－2 ac cs B ＝9＋ c 2－3 c ＝13，即 c 2－3 c －4＝ 0，解得 c ＝－1(舍去)或 c ＝4，∴ c ＝4.故选D.
4. 在△ ABC 中， D 为边 BC 上一点， AD ＝6， BD ＝3，∠ ABC ＝45°，则 sin ∠ ADC 的值为(　C　)
5. [设问创新/多选]黑板上有一道解三角形的习题，求解过程是正确的，但一位同学 不小心把其中一部分擦去了，现在只能看到：在△ ABC 中，内角 A ， B ， C 的对边 分别为 a ， b ， c ，已知 a ＝2，……，解得 B ＝60°.根据以上信息，你认为下面哪个 选项可以作为这个习题的其余已知条件？(　ABD　)
6. [多选]在△ ABC 中，内角 A ， B ， C 的对边分别为 a ， b ， c ，下列条件能判断△ ABC 是钝角三角形的有(　BC　)
解法二　延长 AD 到 E 使 AD ＝ DE ，连接 BE ， CE ，则四边形 ABEC 是平行四边 形， AE ＝2 AD ，所以 AE 2＋ BC 2＝2( AB 2＋ AC 2)，所以 BC 2＝14＞ AB 2＋ AC 2，则 △ ABC 为钝角三角形.故选C.
12. [2024湖北部分学校联考]在△ ABC 中，角 A ， B ， C 的对边分别为 a ， b ， c ， b ＝3， BD 为 AC 边上的中线， BD ＝2，且 a cs C －2 b cs ∠ ABC ＋ c cs A ＝0，则 △ ABC 的面积为(　C　)
13. [多选]在△ ABC 中，内角 A ， B ， C 所对的边分别为 a ， b ， c ，已知( b ＋ c )∶( c ＋ a )∶( a ＋ b )＝4∶5∶6，则下列结论正确的是(　ABD　)
(1)求△ ABC 的面积；
(2)若 DC ＝ DA ，求△ ADC 的周长.
(1)求角 B 的大小；
(2)已知 c ＝ b ＋1，且角 A 有两解，求 b 的取值范围.
16. [情境创新]剪纸，又叫刻纸，是一种镂空艺术，是中国最古老的民间艺术之一.如 图， 纸片为一圆形，直径 AB ＝20 cm，需要剪去四边形 CEC 1 D ，可以经过对折、 沿 DC 和 EC 裁剪、展开得到.
已知点 C 在圆上且 AC ＝10 cm，∠ ECD ＝30°.要使得镂空的四边形 CEC 1 D 面积最 小， AD 的长应为 ⁠cm.