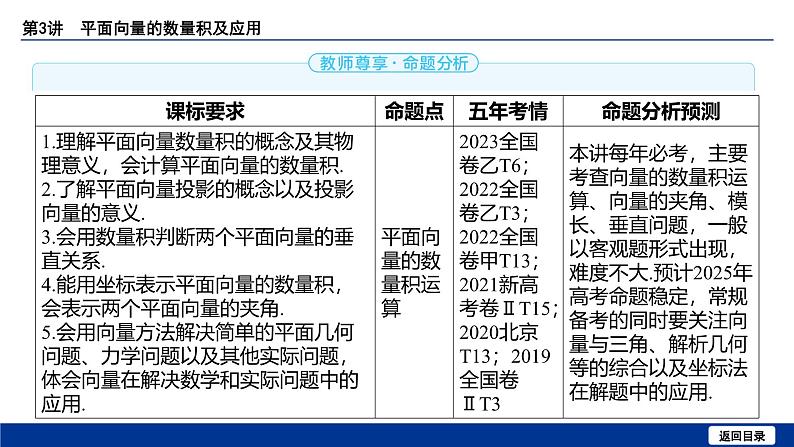
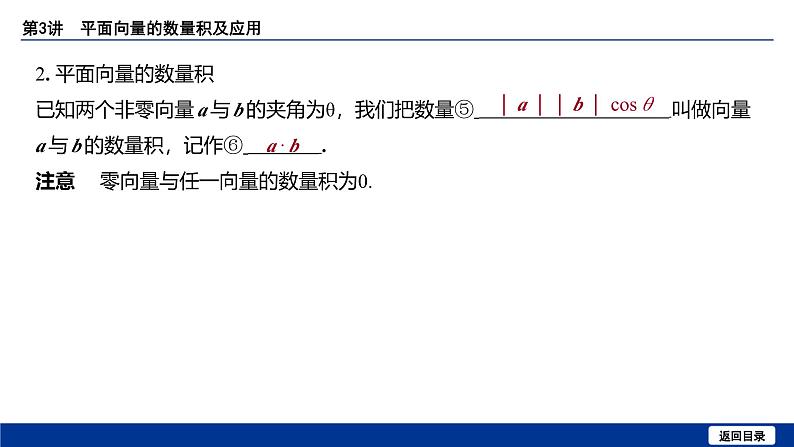
备战2025年高考数学精品课件第六章 第3讲 平面向量的数量积及应用

这是一份备战2025年高考数学精品课件第六章 第3讲 平面向量的数量积及应用，共60页。
注意　 确定向量的夹角时应注意“共起点”.
2. 平面向量的数量积已知两个非零向量 a 与 b 的夹角为θ，我们把数量⑤ 叫做向量 a 与 b 的数量积，记作⑥ ⁠.注意　 零向量与任一向量的数量积为0.
｜ a ｜｜ b ｜ cs θ　
4. 向量数量积的运算律对于向量 a ， b ， c 和实数λ，有(1) a · b ＝ b · a ；(2)(λ a )· b ＝λ( a · b )＝ a ·(λ b )；(3)( a ＋ b )· c ＝ a · c ＋ b · c .
注意　 (1)向量数量积的运算不满足乘法结合律，即( a · b )· c 不一定等于 a ·( b · c )， 这是由于( a · b )· c 表示一个与 c 共线的向量， a ·( b · c )表示一个与 a 共线的向量，而 c 与 a 不一定共线.(2) a · b ＝ a · c ( a ≠0)⇏ b ＝ c ，等式两边不能约去同一个向量.(3)平方差公式、完全平方公式仍适用.
5. 平面向量数量积的有关结论
已知非零向量 a ＝( x 1， y 1)， b ＝( x 2， y 2)， a 与 b 的夹角为θ.
x1x2＋y1y2＝0　
x1y2－x2y1＝0　
1. 以下说法正确的是(　A　)
2. [教材改编]已知向量 a ＝(1＋ x ， x －3)， b ＝(1－ x ，2)， a · b ＝－4，则 a ＋2 b 与 b 的夹角为(　B　)
3. [2022全国卷甲]已知向量 a ＝( m ，3)， b ＝(1， m ＋1).若 a ⊥ b ，则 m ＝ ⁠.
5. [易错题]已知平面内三个向量 a ， b ， c 两两夹角相等，且｜ a ｜＝｜ b ｜＝1，｜ c ｜＝3，则｜ a ＋ b ＋ c ｜＝ ⁠.
求非零向量 a ， b 的数量积的方法
1. 定义法： a · b ＝｜ a ｜｜ b ｜ cs θ.
2. 基底法：选取合适的一组基底，利用平面向量基本定理将待求数量积的两个向量 分别表示出来，进而根据数量积的运算律和定义求解.
3. 坐标法：已知条件中有(或隐含)正交基底，优先考虑建立平面直角坐标系，利用 a · b ＝ x 1 x 2＋ y 1 y 2求解.
命题点2　平面向量数量积的应用角度1　向量的模问题例2 (1)[2022全国卷乙]已知向量 a ＝(2，1)， b ＝(－2，4)，则｜ a － b ｜＝ (　D　)
方法技巧求平面向量模的两种方法
[解析]　∵ a ＋ b ＋ c ＝0，∴ c ＝－ a － b ，等式两边同时平方得2＝ a 2＋ b 2＋2 a · b ＝1＋1＋2 a · b ，∴ a · b ＝0.
(2)[2022新高考卷Ⅱ]已知向量 a ＝(3，4)， b ＝(1，0)， c ＝ a ＋ tb ，若＜ a ， c ＞＝ ＜ b ， c ＞，则 t ＝(　C　)
解法二　因为＜ a ， c ＞＝＜ b ， c ＞，且 c ＝ a ＋ tb ，所以由向量加法的平行四边 形法则得｜ a ｜＝ t ｜ b ｜，易知｜ a ｜＝5，｜ b ｜＝1，所以 t ＝5.
求平面向量夹角问题的三种方法
角度3　向量的垂直问题例4 (1)[2023新高考卷Ⅰ]已知向量 a ＝(1，1)， b ＝(1，－1).若( a ＋λ b )⊥( a ＋μ b )， 则(　D　)
[解析]　因为 a ＝(1，1)， b ＝(1，－1)，所以 a ＋λ b ＝(1＋λ，1－λ)， a ＋μ b ＝(1＋ μ，1－μ)，因为( a ＋λ b )⊥( a ＋μ b )，所以( a ＋λ b )·( a ＋μ b )＝0，所以(1＋λ)(1＋μ) ＋(1－λ)(1－μ)＝0，整理得λμ＝－1.故选D.
(2)[全国卷Ⅱ]已知单位向量 a ， b 的夹角为60°，则在下列向量中，与 b 垂直的是 (　D　)
解法二　根据条件，分别作出向量 b 与A，B，C，D四个选项对应的向量的位置关 系，如图所示.
A B C D
由图易知，只有选项D满足题意.故选D.
方法技巧1. 证明两个向量垂直的解题策略先计算出这两个向量的坐标或表示出两个向量，然后根据数量积的运算公式，计算 出这两个向量的数量积为0即可.2. 已知两个向量的垂直关系，求解相关参数的值根据两个向量垂直的充要条件，列出相应的关系式，进而求解参数.
训练2 (1)[2023广州市二检]已知两个非零向量 a ， b 满足｜ a ｜＝3｜ b ｜，( a ＋ b )⊥ b ，则 cs 〈 a ， b 〉＝(　D　)
(2)[2021全国卷甲]若向量 a ， b 满足｜ a ｜＝3，｜ a － b ｜＝5， a · b ＝1，则｜ b ｜ ＝ ⁠.
命题点3　平面向量的应用
例5 在日常生活中，我们会看到两人共提一个行李包的情况(如图).假设行李包所受 重力为 G ，所受的两个拉力分别为 F 1， F 2.若｜ F 1｜＝｜ F 2｜， F 1与 F 2的夹角为 θ，则下列结论不正确的是(　D　)
方法技巧用向量方法解决实际问题的步骤
[解析]　连接 PM ，由题意得，当小货船的航程最短时，其航线为线段 PM .
设小货船航行的速度为 v ，水流的速度为 v 1，水流的速度与小货船航行的速度的合 速度为 v 2，作出示意图，如图所示.
在Rt△ PQM 中，(根据“ PQ 与河流的方向垂直”得到△ PMQ 的形状)
易知 v ＝ v 2－ v 1，｜ v 1｜＝3，｜ v 2｜＝5，
所以小货船航行速度的大小为7 km/h，故选C.
思维帮·提升思维　快速解题
(2)[多选/2023安徽淮北师大附中模拟]数学家欧拉在1765年发表的《三角形的几何 学》一书中有这样一个定理：三角形的重心、垂心和外心共线.这条线就是三角形的 欧拉线.在△ ABC 中， O ， H ， G 分别是外心、垂心和重心， D 为 BC 边的中点，则 下列四个选项中正确的是(　ABD　)
[解析]　根据题意画出图形，如图所示.
3. [2023吉林长春质监]已知向量 a 与 b 的夹角为60°，｜ a ｜＝2，｜ b ｜＝1，则｜ a －2 b ｜＝(　C　)
4. 已知单位向量 a ， b 满足｜ a ＋ b ｜＞1，则 a 与 b 夹角的取值范围是(　B　)
5. [2023河南安阳模拟]已知 a ＝(1，0)， b ＝(0，1)， c ＝ a ＋ tb ， t ∈R，若 sin ＜ a ， c ＞＝ sin ＜ b ， c ＞，则 t ＝(　B　)
[解析]　｜2 a － b ｜2＝(2 a － b )2＝4｜ a ｜2－4｜ a ｜·｜ b ｜ cs ＜ a ， b ＞＋｜ b ｜2＝4－2｜ b ｜＋｜ b ｜2＝3，解得｜ b ｜＝1.
9. [2021新高考卷Ⅱ]已知向量 a ＋ b ＋ c ＝0，｜ a ｜＝1，｜ b ｜＝｜ c ｜＝2， a · b ＋ b · c ＋ c · a ＝ ⁠.
10. 已知单位向量 a ， b 满足｜ a －2 b ｜＝3 a · b ，则向量 a ， b 夹角的余弦值 为 ⁠.
[－11，－9]