备战2025年高考数学精品课件第五章 突破3 数列中的创新型问题

这是一份备战2025年高考数学精品课件第五章 突破3 数列中的创新型问题，共32页。PPT课件主要包含了ABD，故选B等内容，欢迎下载使用。
命题点1　数学文化情境下的数列应用
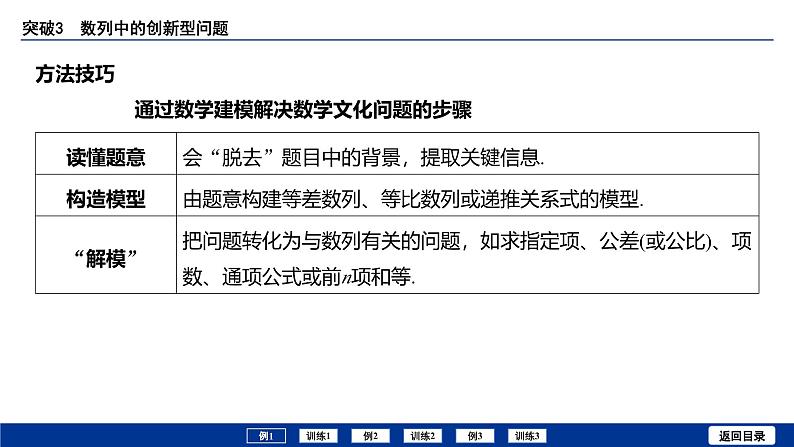
方法技巧通过数学建模解决数学文化问题的步骤
训练1 [2023安徽名校联考]“物不知数”原载于《孙子算经》，它的系统解法是南宋 数学家秦九韶在《数书九章·大衍求一术》中给出的.“大衍求一术”是中国古算中 最具独创性的成就之一，属现代数论中的一次同余式组问题.现有一道同余式组问 题：将正整数中，被4除余1且被6除余3的数，按由小到大的顺序排成一列，构成数 列{ an }，记{ an }的前 n 项和为 Sn ，则 S 10＝(　C　)
命题点2　现代生活情境下的数列应用例2 某市抗洪指挥部接到最新雨情预报，未来24 h城区拦洪坝外洪水将超过警戒水 位，因此需要紧急抽调工程机械加高加固拦洪坝.经测算，加高加固拦洪坝工程需要 调用20辆某型号翻斗车，平均每辆翻斗车需要工作24 h.而抗洪指挥部目前只有一辆 翻斗车可立即投入施工，其余翻斗车需要从其他施工现场抽调.若抽调的翻斗车每隔 20 min才有一辆到达施工现场投入工作，要在24 h内完成拦洪坝加高加固工程，指 挥部至少还需要抽调这种型号翻斗车(　C　)
训练2 [多选]如图所示，这是小朋友们喜欢玩的彩虹塔叠叠乐玩具.某数学兴趣小组 利用该玩具制订如下玩法：在2号杆中自下而上串有由大到小的 n ( n ∈N*)个彩虹 圈，将2号杆中的彩虹圈全部移动到1号杆中，3号杆可以作为过渡使用；每次只能 移动一个彩虹圈，且无论在哪个杆中，小的彩虹圈必须放置在大的上方；将一个彩 虹圈从一个杆移动到另一个杆中记为移动1次，记 an 为2号杆中 n 个彩虹圈全部移动 到1号杆所需要的最少移动次数，设 bn ＝ an ＋1－ n ，则下面结论正确的是(　ABD　)
[解析]　由题意易得， a 1＝1， a 2＝3.易知将 n ＋1个彩虹圈全部移动到1号杆中所需 要的最少次数为 an ＋1，若要将2号杆中的 n ＋1个彩虹圈全部移动到1号杆中，则第 一步，将除了最大的彩虹圈的 n 个彩虹圈全部移动到3号杆中，所需要移动的最少次 数为 an ；第二步，将最大的彩虹圈移动到1号杆中，最少需要移动1次；第三步，将 3号杆中的 n 个彩虹圈全部移动到1号杆中，需要移动的最少次数为 an ，所以 an ＋1＝ 2 an ＋1，所以 an ＋1＋1＝2( an ＋1).又 a 1＋1＝2，所以数列{ an ＋1}是以2为首项，2 为公比的等比数列，所以 an ＋1＝2 n ， an ＝2 n －1， a 3＝7，所以选项A，B均正确； 因为 bn ＝ an ＋1－ n ，所以 bn ＝2 n ＋1－1－ n ，所以选项C错误；
命题点3　数列中的新定义问题
训练3 函数 y ＝[ x ]称为高斯函数，[ x ]表示不超过 x 的最大整数，如[0.9]＝0，[lg 99] ＝1.已知数列{ an }满足 a 3＝3，且 an ＝ n ( an ＋1－ an )，若 bn ＝[lg an ]，则数列{ bn }的 前2 025项和为 ⁠.
1. [命题点1/2023河南郑州一模]我国古代有这样一个数学问题：今有男子善走，日增 等里，首日行走一百里，九日共行一千二百六十里，问日增几何？其大意是：现有 一个善于步行的人，第一天行走了一百里，以后每天比前一天多走 d 里，九天他一 共行走了一千二百六十里，求 d 的值.关于该问题，下列结论错误的是(　A　)
3. [命题点3/多选/2023北京师范大学第二附属中学期中]若一个数列的第 m 项等于这 个数列的前 m 项的乘积，则称这个数列为“ m 积特征列”，若各项均为正数的等比 数列{ an }为“6积特征列”，且 a 1＞1，则当{ an }的前 n 项之积最大时， n 的值为 (　CD　)
1. [2023武汉市5月模拟]将1，2，…， n 按照某种顺序排成一列得到数列{ an }，对任 意1≤ i ＜ j ≤ n ，如果 ai ＞ aj ，那么称数对( ai ， aj )构成数列{ an }的一个逆序对.若 n ＝4，则恰有2个逆序对的数列{ an }的个数为(　B　)
[解析]　由题知数列{ an }中的项都是正整数，当 n ＝4时，1≤ i ＜ j ≤4，将1，2， 3，4按照某种顺序排成一列，则用列举法列出所有恰有2个逆序对的数列的组合为 {1，4，2，3}，{1，3，4，2}，{2，1，4，3}，{2，3，1，4}，{3，1，2，4}，共5 个，故选B.
5. 我国古人将一年分为二十四个节气，如图所示，相邻两个节气晷长减少或增加的 量相同，冬至的晷长最长，夏至的晷长最短，周而复始.已知冬至的晷长为13.5尺， 芒种的晷长为2.5尺，则一年中夏至到大雪的晷长的和为 尺.
6. 某项测试有10道必答题，甲和乙参加该测试，分别用数列{ an }和{ bn }记录他们的 成绩.若第 k 题甲答对，则 ak ＝ k ，若第 k 题甲答错，则 ak ＝－ k ；若第 k 题乙答对， 则 bk ＝2 k －1 ，若第 k 题乙答错，则 bk ＝－2 k －1.已知 b 1＋ b 2＋…＋ b 10＝767， a 1 b 1 ＋ a 2 b 2＋…＋ a 10 b 10＝9 217，则 a 1＋ a 2＋…＋ a 10＝ ⁠.
(1)求{ an }的通项公式.