备战2025年高考数学精品课件第五章 第2讲 等差数列

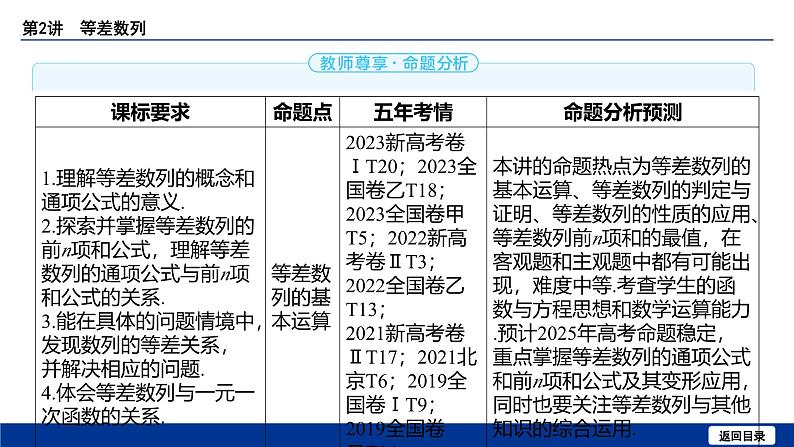
这是一份备战2025年高考数学精品课件第五章 第2讲 等差数列，共60页。PPT课件主要包含了一个常数，等差中项，规律总结，等差数列的单调性，等差数列的性质，最小公倍数，方法技巧，BCD，A15，B30等内容，欢迎下载使用。
1. 等差数列的概念(1)等差数列的定义一般地，如果一个数列从第2项起，每一项与它的前一项的① 都等于② ⁠ ⁠，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差 通常用字母 d 表示.(2)等差中项如果 a ， A ， b 成等差数列，那么 A 叫做 a 与 b 的③ ，且 A ＝ ④ ⁠.
(3)等差数列的通项公式及其变形
通项公式：⑤ ，其中 a 1是首项， d 是公差.
通项公式的变形： an ＝ am ＋( n － m ) d ( m ， n ∈N*).
说明　 由 an ＝ dn ＋( a 1－ d )可知，当 d ≠0时， an 可看作关于 n 的一次函数.
an ＝ a 1＋( n －1) d 　
当 d ＞0时，数列{ an }为递增数列；当 d ＜0时，数列{ an }为递减数列；当 d ＝0时， 数列{ an }为常数列.
2. 等差数列的前 n 项和
(1)等差数列项的性质
设数列{ an }，{ bn }均为等差数列.
a.若 k ＋ l ＝ m ＋ n ( k ， l ， m ， n ∈N*)，则 ak ＋ al ＝ am ＋ an ，特别地，若 p ＋ q ＝ 2 m ，则⑦ .反之不一定成立.
b.若{ an }公差为 d ，则{ a 2 n }也是等差数列，公差为⑧ ⁠.
c .{ pan ＋ qbn }( p ， q 为常数)也是等差数列.
d.若{ an }与{ bn }有公共项，则{ an }与{ bn }的公共项从小到大排成的新数列也是等差 数列，首项是第一个相同的公共项，公差是{ an }与{ bn }的公差的⑨ ⁠ ⁠.
ap ＋ aq ＝2 am 　
e.若{ an }公差为 d ，则 ak ， ak ＋ m ， ak ＋2 m ，…( k ， m ∈N*)组成公差为⑩ ⁠的 等差数列，即下标成等差数列，则相应的项也成等差数列.
(2)等差数列前 n 项和的性质
设 Sn 为等差数列{ an }的前 n 项和.
b. Sm ， S 2 m － Sm ， S 3 m － S 2 m ，…( m ∈N*)是等差数列.
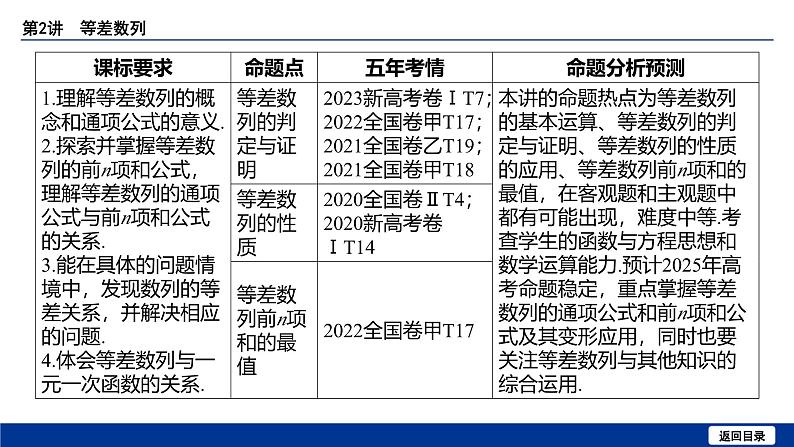
1. [教材改编]如果三角形的三个内角成等差数列，则中间角的大小为 ⁠.
[解析]　由题意可设三个内角分别为 x － d ， x ， x ＋ d ，则有( x － d )＋ x ＋( x ＋ d ) ＝180°，可得 x ＝60°.
2. 若等差数列{ an }满足 a 7＋ a 8＋ a 9＞0， a 7＋ a 10＜0，则当 n ＝ 时，{ an }的 前 n 项和最大.
[解析]　由 a 7＋ a 8＋ a 9＞0可得 a 8＞0，由 a 7＋ a 10＜0可得 a 8＋ a 9＜0，所以 a 9＜ 0，所以当 n ＝8时，{ an }的前 n 项和最大.
3. [教材改编]已知{ an }为等差数列，且 a 20＝30， a 30＝20，则 a 50＝ ⁠.
4. [教材改编]某公司购置了一台价值220万元的设备，随着设备在使用过程中老化， 每经过一年，其价值减少20万元.当设备价值低于购进价值的5％时，设备将报废， 则该机器最多使用 年.
[解析]　设使用 n 年后，该设备的价值为 an 万元，则易知{ an }是以(220－20)为首 项，－20为公差的等差数列，所以 an ＝(220－20)＋( n －1)×(－20)＝220－20 n .令 220－20 n ≥220×5％，得 n ≤10.45，所以该设备最多使用10年.
5. 已知等差数列{ an }的项数为奇数，其中所有奇数项和为290，所有偶数项和为 261，则该数列的项数为 ⁠.
6. [易错题]已知数列{ an }满足 a 1＝1， an ＋ an ＋1＝ n ，则 a 20＝ ⁠.
[解析]　因为 an ＋ an ＋1＝ n ，所以 a 1＋ a 2＝1， a 2＋ a 3＝2，…， a 19＋ a 20＝19.因为 a 1＝1，所以可得 a 1＝1， a 3＝2， a 5＝3， a 7＝4，…，和 a 2＝0， a 4＝1， a 6＝2， a 8＝3，…，奇数项、偶数项分别构成等差数列，所以 a 2 k ＝ k －1( k ∈N*)，所以 a 20 ＝10－1＝9.
命题点1　等差数列的基本运算
例1 [2023全国卷甲]记 Sn 为等差数列{ an }的前 n 项和.若 a 2＋ a 6＝10， a 4 a 8＝45，则 S 5＝(　C　)
(1)若3 a 2＝3 a 1＋ a 3， S 3＋ T 3＝21，求{ an }的通项公式；
(2)若{ bn }为等差数列，且 S 99－ T 99＝99，求 d .
1. 等差数列基本运算中常用的数学思想
2. 等差数列基本运算中常用的设元技巧
若三个数成等差数列，可将三个数设为 a － d ， a ， a ＋ d ；若四个数成等差数列， 可将四个数设为 a －3 d ， a － d ， a ＋ d ， a ＋3 d .
(2)[2022全国卷乙]记 Sn 为等差数列{ an }的前 n 项和.若2 S 3＝3 S 2＋6，则公差 d ＝ ⁠.
[解析]　因为2 S 3＝3 S 2＋6，所以2(3 a 1＋3 d )＝3(2 a 1＋ d )＋6，化简得3 d ＝6，解 得 d ＝2.
命题点2　等差数列的判定与证明
例3 [2021全国卷甲]已知数列{ an }的各项均为正数，记 Sn 为{ an }的前 n 项和，从下 面①②③中选取两个作为条件，证明另外一个成立.
等差数列的判定与证明的方法
(2)[多选/2023福建莆田九中质检]已知数列{ an }的前 n 项和为 Sn ，则下列结论正确的 是(　BCD　)
命题点3　等差数列的性质
例4 (1)[新高考卷Ⅰ]将数列{2 n －1}与{3 n －2}的公共项从小到大排列得到数列 { an }，则{ an }的前 n 项和为 ⁠.
3 n 2－2 n 　
训练3 (1)数列{ an }，{ bn }均为等差数列，且 a 1＝－5， b 1＝－15， a 2 025＋ b 2 025＝ 100，则数列{ an ＋ bn }的前2 025项和为 ⁠.
命题点4　等差数列前 n 项和的最值
(1)证明：{ an }是等差数列.
(2)若 a 4， a 7， a 9成等比数列，求 Sn 的最小值.
求等差数列前 n 项和 Sn 的最值的方法
训练4 等差数列{ an }的前 n 项和为 Sn ，若∀ n ∈N*， Sn ≤ S 7，则数列{ an }的通项公 式可能是 (　B　)
[解析]　因为数列{ an }是等差数列，且∀ n ∈N*， Sn ≤ S 7，所以该数列从第8项起为 非正数，即 a 7≥0， a 8≤0.对于A， a 7＝16－3×7＝－5＜0，故A不正确；对于B， a 7＝15－2×7＝1＞0， a 8 ＝15－2×8＝－1＜0，故B正确；对于C， a 7＝2×7－14＝0， a 8＝2×8－14＝2＞ 0，故C不正确；对于D， a 7＝2×7－15＝－1＜0，故D不正确.故选B.
1. [命题点1/2021新高考卷Ⅱ]记 Sn 是公差不为0的等差数列{ an }的前 n 项和，若 a 3＝ S 5， a 2 a 4＝ S 4.
(1)求数列{ an }的通项公式；
(2)求使 Sn ＞ an 成立的 n 的最小值.
2. [命题点2/多选]两个等差数列{ an }和{ bn }，其公差分别为 d 1 和 d 2 ，其前 n 项和分 别为 Sn 和 Tn ，则下列说法正确的是(　AB　)
(1)证明：数列{ bn }是等差数列.
(2)求{ an }的通项公式.
1. [2024河南名校模拟]设 Sn 是等差数列{ an }的前 n 项和，若 a 2＋ a 5＋ a 8＝15，则 S 9 ＝(　C　)
3. [2024吉林白城模拟]已知等差数列{ an }是递增数列，且满足 a 3＋ a 5＝14， a 2 a 6＝ 33，则 a 1 a 7＝(　C　)
4. [2023陕西宝鸡模拟]已知首项为2的等差数列{ an }的前30项中，奇数项的和为 A ， 偶数项的和为 B ，且 B － A ＝45，则 an ＝(　B　)
[解析]　在等差数列{ an }中，首项 a 1＝2，设其公差为 d ，由前30项中奇数项的和为 A ， 偶数项的和为 B ， 且 B － A ＝45，可得－ a 1＋ a 2－…－ a 29＋ a 30＝15 d ＝45， 解得 d ＝3，∴ an ＝ a 1＋( n －1) d ＝2＋3( n －1)，即 an ＝3 n －1，故选B.
5. [多选/2024山东模拟]已知等差数列{ an }的前 n 项和为 Sn ，公差为 d ， a 3＝ a 1－ 4， S 7＝154，则(　AC　)
6. [2023广州市二检]在数列{ an }中， a 1＝2， am ＋ n ＝ am ＋ an ( m ， n ∈N*)，若 akak ＋1＝440，则正整数 k ＝ ⁠.
[解析]　解法一　令 m ＝1，则 an ＋1＝ an ＋ a 1，即 an ＋1－ an ＝2，所以数列{ an }是 以2为首项，2为公差的等差数列，即 an ＝2＋( n －1)×2＝2 n ，又 k 为正整数，所以 akak ＋1＝2 k ×2( k ＋1)＝440，即 k ( k ＋1)＝110，解得 k ＝10或 k ＝－11(舍去).故填 10.
解法二(列举法)　令 m ＝ n ＝1，则 a 2＝ a 1＋ a 1＝4；令 m ＝1， n ＝2，则 a 3＝ a 1＋ a 2＝6；令 m ＝ n ＝2，则 a 4＝ a 2＋ a 2＝8.通过观察找规律可知，数列{ an }是以2为 首项，2为公差的等差数列，即 an ＝2＋( n －1)×2＝2 n ，又 k 为正整数，所以 akak ＋1＝2 k ×2( k ＋1)＝440，即 k ( k ＋1)＝110，解得 k ＝10或 k ＝－11(舍去).故填10.
7. [2024江西抚州模拟改编]在数列{ an }中，已知 an ＋1－ an ＝ an ＋2－ an ＋1， a 1 013＝ 1，则该数列前2 025项的和 S 2 025＝ ⁠.
9. [2024浙江普陀中学模拟]已知正项数列{ an }的前 n 项和为 Sn ， a 1＝2.
10. [2024四川南充校考]若一个凸 n ( n ∈N*)边形的最小内角为95°，其他内角依次增 加10°，则 n 的值为(　B　)
11. [2024湖北孝感高中模拟]设等差数列{ an }的前 n 项和为 Sn ，满足2 a 3－ a 5＝7， a 2＋ S 7＝12，则 Sn 的最大值为(　B　)
12. [全国卷Ⅱ]北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层.上层中心有 一块圆形石板(称为天心石)，环绕天心石砌9块扇面形石板构成第一环，向外每环依 次增加9块.下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块.已 知每层环数相同，且下层比中层多729块，则三层共有扇面形石板(不含天心 石)(　C　)
2 n －1(答案
14. 已知正项数列{ an }，其前 n 项和 Sn 满足 an (2 Sn － an )＝1( n ∈N*).