备战2025年高考数学精品课件大题规范6 概率与统计

这是一份备战2025年高考数学精品课件大题规范6 概率与统计，共14页。PPT课件主要包含了规范答题等内容，欢迎下载使用。
学生用书P256考情综述　概率与统计解答题，每年必考，难度中等或中等偏上.该类问题以真实情 境为载体，注重考查学生的应用意识、阅读理解能力以及数据分析、数学建模和数 学运算素养，充分体现了概率与统计的工具性和综合性.从近几年的命题情况看，命题热点有(1)概率问题，核心是概率计算及离散型随机变 量的分布列与期望的求解，其中互斥、对立、相互独立事件的概率，条件概率，全 概率是概率计算的核心，排列组合是进行概率计算的工具；(2)统计问题，核心是样 本数据的获得及分析方法，重点是统计图表的应用，样本的数字特征、一元线性回 归模型及独立性检验；(3)概率与统计的综合，概率统计与其他知识(如函数、数列) 的综合.具体解题时，需要先过“审题关”，再过“公式关”，最后过“运用关”，否则， 极易出现错误，导致“会而不对”.
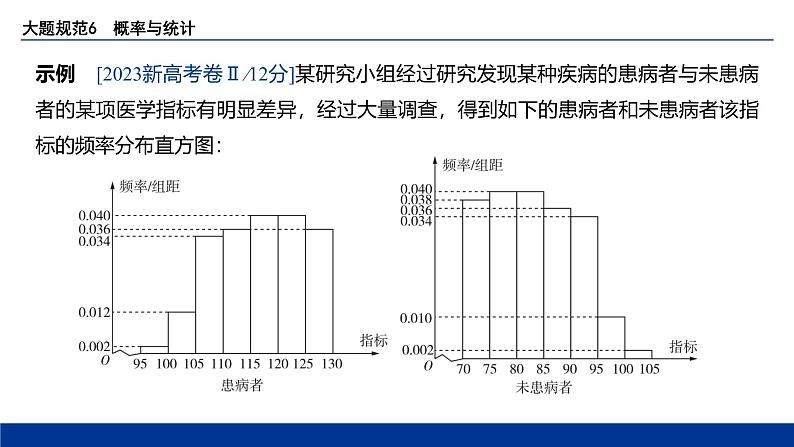
示例　[2023新高考卷Ⅱ/12分]某研究小组经过研究发现某种疾病的患病者与未患病 者的某项医学指标有明显差异，经过大量调查，得到如下的患病者和未患病者该指 标的频率分布直方图：
利用该指标制定一个检测标准，需要确定临界值 c ，将该指标大于 c 的人判定为阳 性，小于或等于 c 的人判定为阴性，此检测标准的漏诊率是将患病者判定为阴性的 概率，记为 p ( c )；误诊率是将未患病者判定为阳性的概率，记为 q ( c ).假设数据在 组内均匀分布.以事件发生的频率作为相应事件发生的概率.(1)当漏诊率 p ( c )＝0.5％时，求临界值 c 和误诊率 q ( c )；(2)设函数 f ( c )＝ p ( c )＋ q ( c ).当 c ∈[95，105]时，求 f ( c )的解析式，并求 f ( c )在区 间[95，105]的最小值.
(1)由题中患病者该指标的频率分布直方图知(100－95)×0.002＝1％＞0.5％，所以95 ＜ c ＜100，
设 X 为患病者的该指标，
则 p ( c )＝ P ( X ≤ c )＝( c －95)×0.002＝0.5％，解得 c ＝97.5.
设 Y 为未患病者的该指标，
则 q ( c )＝ P ( Y ＞ c )＝(100－97.5)×0.01＋5×0.002＝0.035＝3.5％.
(4分) →注意题眼“误诊率是将未患病者判定为阳性的概”，故需利用未患病者该指标的频率分布直方图求出 Y ＞ c 的频率.
(2)当95≤ c ≤100时， p ( c )＝( c －95)×0.002＝0.002 c －0.19，
q ( c )＝(100－ c )×0.01＋5×0.002＝－0.01 c ＋1.01，
所以 f ( c )＝ p ( c )＋ q ( c )＝－0.008 c ＋0.82；
当100＜ c ≤105时，
p ( c )＝5×0.002＋( c －100)×0.012＝0.012 c －1.19，
q ( c )＝(105－ c )×0.002＝－0.002 c ＋0.21，
所以 f ( c )＝ p ( c )＋ q ( c )＝0.01 c －0.98. (8分)
(6分) →观察患病者和未患病者该指标的频率分布直方图，需对 c 分两类(95≤ c ≤100与100＜ c ≤105)讨论.
由一次函数的单调性知，函数 f ( c )在[95，100]上单调递减，在(100，105]上 单调递增，
作出 f ( c )在区间[95，105]上的大致图象(略)，可得 f ( c )在区间[95，105]上的最小值 f ( c )min＝ f (100)＝－0.008×100＋0.82＝0.02. (12分)
(10分) → f ( c )的[解析]式要写成分段形式.
感悟升华1. 解答概率与统计问题重在“辨”——辨析、辨型
(2)若前三局比赛中甲只赢了一局，设这场比赛结束还需要比赛的局数为ξ，求ξ的分 布列和数学期望 f ( p )，并求当 p 为何值时， f ( p )最大.