备战2025年高考数学精品课件大题规范1 函数与导数

这是一份备战2025年高考数学精品课件大题规范1 函数与导数，共14页。
　 函数与导数解答题，难度较大，从其在2023年新高考卷Ⅰ中的位置来看， 难度有所下降，说明难度定位更灵活.从近几年的命题情况来看，常涉及的背景函数有：指数函数、对数函数、分式函 数、三次函数、三角函数.涉及的命题点有：求切线方程，判断单调性，求单调区 间、极值、最值、参数范围，零点问题，证明不等式问题，不等式恒成立问题等.常 涉及的数学思想有：函数与方程思想、分类讨论思想、数形结合思想、转化与化归 思想等.解题时，无论是单调性、极值、最值问题还是不等式问题，一般需要先求出函数的 导数，然后通过导数研究函数的单调性来求解，因此掌握导数与函数的单调性的关 系尤为重要.求解过程中，注意内容书写的规范性和完整性.
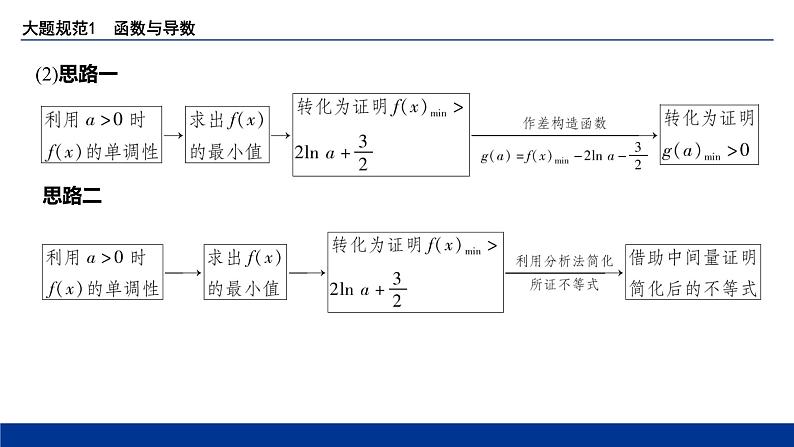
(2)思路一　
思路二　
(1)因为 f ( x )＝ a (e x ＋ a )－ x ，所以f'( x )＝ a e x －1，(1分) 正确求导是关键.
当 a ≤0时，f'( x )＜0，所以函数 f ( x )在(－∞，＋∞)上单调递减；(2分) 注意单调区间的范围.
当 a ＞0时，令f'( x )＜0，得 x ＜－ln a ，令f'( x )＞0，得 x ＞－ln a ，所以函数 f ( x )在(－∞，－ln a )上单调递减，在(－ln a ，＋∞)上单调递增.(4分) 有一处不等式解错，但单调性判断对，这一步只给1分.
综上可得：当 a ≤0时，函数 f ( x )在(－∞，＋∞)上单调递减；当 a ＞0时，函数 f ( x )在(－∞，－ln a )上单调递减，在(－ln a ，＋∞)上单调递增. (5分) 下结论不可少，否则，就会失去结论分.
(2)解法一(最值法)　由(1)得，当 a ＞0时，函数 f ( x )＝ a (e x ＋ a )－ x 的最小值为 f (－ln a )＝ a (e－ln a ＋ a )＋ln a ＝1＋ a 2＋ln a ，(6分) 第(1)问中没有别的条件，其结论可以在第(2)问中合理使用.
解法二(分析法)　当 a ＞0时，由(1)得， f ( x )min＝ f (－ln a )＝1＋ a 2＋ln a ，(6分) 第(1)问没有别的条件，其结论可以在第(2)问中合理利用.
构造函数 u ( a )＝ln a －( a －1)( a ＞0)，
所以函数 u ( a )在(1，＋∞)上单调递减，在(0，1)上单调递增，所以 u ( a )≤ u (1)＝0，即ln a ≤ a －1，(9分) 根据函数 u ( a )的单调性，可得出 u ( a )的最大值.
函数与导数问题的答题策略1. 定义域优先.在利用导数讨论函数的单调性时，要先确定函数的定义域，求单调区 间必须在定义域内进行.2. 正确运用公式与法则.熟练利用基本初等函数的求导公式与法则，正确求导是解题 的关键.注意对复合函数求导法则的运用.3. 分类讨论做到不重不漏.分类讨论是难点，需明晰分类的标准，要做到合理分类， 不重不漏.4. 会构造函数.正确构造函数，利用导数判断新构造函数的单调性，利用函数的性质 求解.5. 会转化.会把不等式问题转化为函数的最值问题，会分离参数或用分析法转化，简 化后求解.
[12分]已知函数 f ( x )＝ x 2－ a (ln x － a ).(1)讨论 f ( x )的单调性；