沪科版数学八上同步提升练习专题16.7 期末专项复习之轴对称图形与等腰三角形二十个必考点（2份，原卷版+解析版）

这是一份沪科版数学八上同步提升练习专题16.7 期末专项复习之轴对称图形与等腰三角形二十个必考点（2份，原卷版+解析版），文件包含沪科版数学八上同步提升练习专题167期末专项复习之轴对称图形与等腰三角形二十个必考点原卷版doc、沪科版数学八上同步提升练习专题167期末专项复习之轴对称图形与等腰三角形二十个必考点解析版doc等2份试卷配套教学资源，其中试卷共143页， 欢迎下载使用。

TOC \ "1-3" \h \u
\l "_Tc24579" 【考点1 轴对称中坐标与图形变化】 PAGEREF _Tc24579 \h 1
\l "_Tc3633" 【考点2 格点中的轴对称】 PAGEREF _Tc3633 \h 2
\l "_Tc2790" 【考点3 设计轴对轴图案】 PAGEREF _Tc2790 \h 3
\l "_Tc25789" 【考点4 镜面对称】 PAGEREF _Tc25789 \h 5
\l "_Tc30274" 【考点5 利用轴对称求最值】 PAGEREF _Tc30274 \h 5
\l "_Tc30658" 【考点6 寻找构成等腰三角形的点的个数】 PAGEREF _Tc30658 \h 6
\l "_Tc22407" 【考点7 利用三线合一求值】 PAGEREF _Tc22407 \h 7
\l "_Tc14366" 【考点8 利用三线合一证明】 PAGEREF _Tc14366 \h 8
\l "_Tc20631" 【考点9 利用等角对等边证明边长相等】 PAGEREF _Tc20631 \h 9
\l "_Tc27294" 【考点10 利用等角对等边证明】 PAGEREF _Tc27294 \h 10
\l "_Tc31648" 【考点11 作等腰三角形】 PAGEREF _Tc31648 \h 12
\l "_Tc20235" 【考点12 等边三角形的判定与性质】 PAGEREF _Tc20235 \h 13
\l "_Tc5734" 【考点13 含30度的直角三角形】 PAGEREF _Tc5734 \h 15
\l "_Tc15530" 【考点14 尺规作垂直平分线或垂线】 PAGEREF _Tc15530 \h 16
\l "_Tc20818" 【考点15 垂直平分线的判定与性质】 PAGEREF _Tc20818 \h 17
\l "_Tc18352" 【考点16 等腰三角形中的新定义问题】 PAGEREF _Tc18352 \h 19
\l "_Tc10112" 【考点17 尺规作图作角平分线】 PAGEREF _Tc10112 \h 22
\l "_Tc24450" 【考点18 角平分线的判定与性质的综合求值】 PAGEREF _Tc24450 \h 23
\l "_Tc4248" 【考点19 角平分线的判定与性质的综合证明】 PAGEREF _Tc4248 \h 24
\l "_Tc5042" 【考点20 角平分线的实际应用】 PAGEREF _Tc5042 \h 26
【考点1 轴对称中坐标与图形变化】
【例1】（2022·贵州省遵义市第一初级中学八年级阶段练习）已知点和关于轴对称，则__．
【变式1-1】（2022·内蒙古·霍林郭勒市第五中学七年级期中）将点A先向下平移3个单位，再向右平移2个单位后得B（﹣2，5），则A点关于y轴的对称点坐标为__________．
【变式1-2】（2022·全国·八年级专题练习）已知点P（2a+b，-3a）与点P′（8，b+2）．
(1)若点p与点p′关于x轴对称，求a、b的值．
(2)若点p与点p′关于y轴对称，求a、b的值．
【变式1-3】（2022·吉林白山·八年级期末）在坐标平面上有一个轴对称图形，其中A（3，﹣）和B（3，﹣）是图形上的一对对称点，若此图形上另有一点C（﹣2，﹣9），则C点对称点的坐标是（ ）
A．（﹣2，1）B．（﹣2，﹣）C．（﹣，﹣9）D．（﹣2，﹣1）
【考点2 格点中的轴对称】
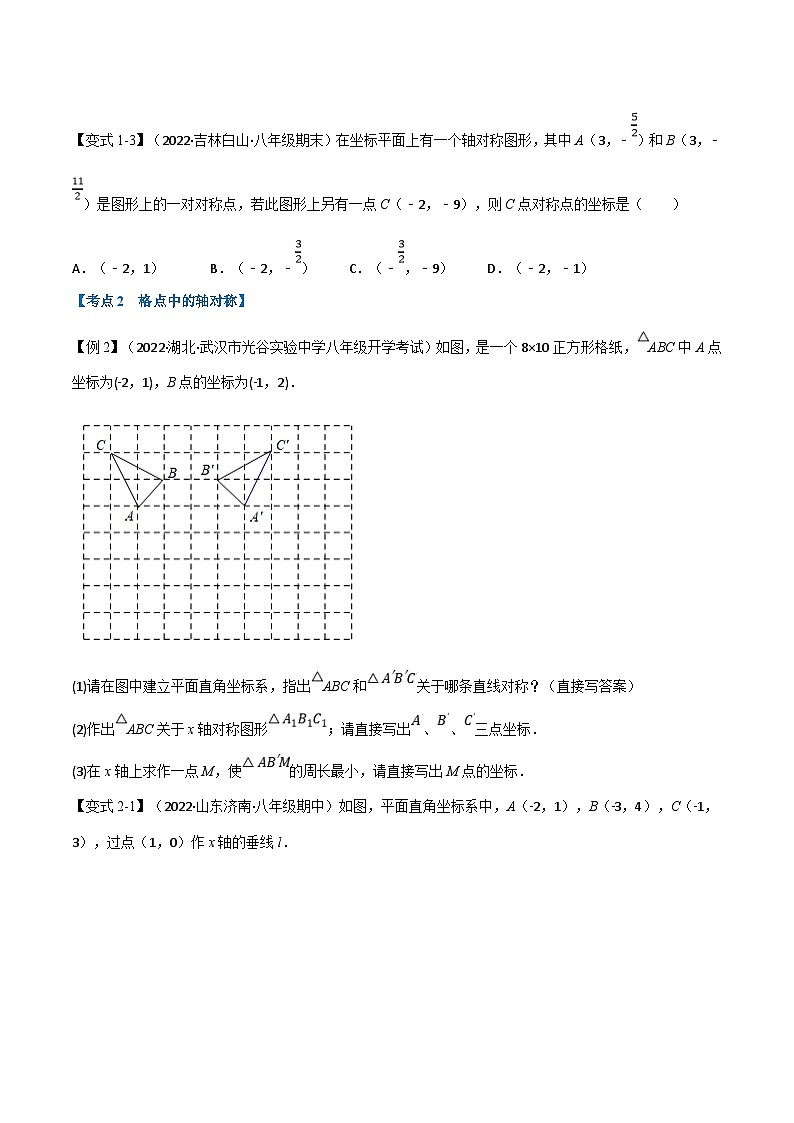
【例2】（2022·湖北·武汉市光谷实验中学八年级开学考试）如图，是一个8×10正方形格纸，ABC中A点坐标为(﹣2，1)，B点的坐标为(﹣1，2)．
(1)请在图中建立平面直角坐标系，指出ABC和关于哪条直线对称？（直接写答案）
(2)作出ABC关于x轴对称图形；请直接写出、、三点坐标．
(3)在x轴上求作一点M，使的周长最小，请直接写出M点的坐标．
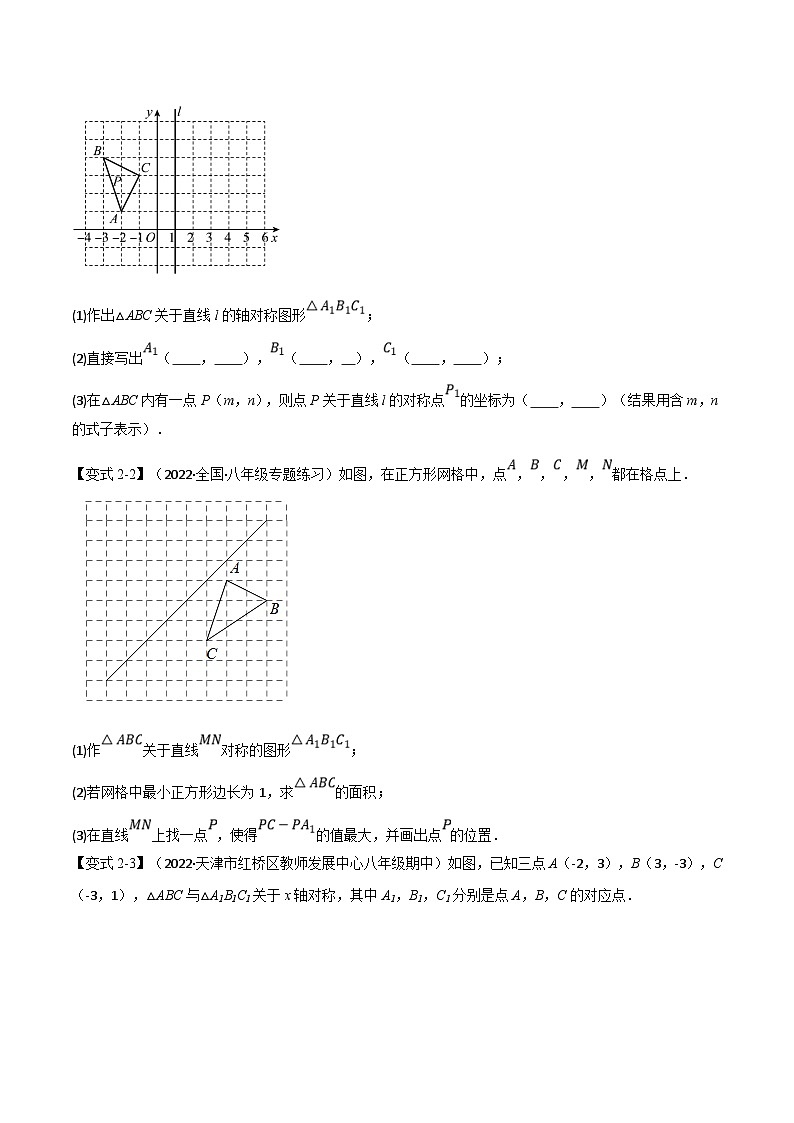
【变式2-1】（2022·山东济南·八年级期中）如图，平面直角坐标系中，A（﹣2，1），B（﹣3，4），C（﹣1，3），过点（1，0）作x轴的垂线l．
(1)作出△ABC关于直线l的轴对称图形；
(2)直接写出（ ， ），（ ， ），（ ， ）；
(3)在△ABC内有一点P（m，n），则点P关于直线l的对称点的坐标为（ ， ）（结果用含m，n的式子表示）．
【变式2-2】（2022·全国·八年级专题练习）如图，在正方形网格中，点，，，，都在格点上．
(1)作关于直线对称的图形；
(2)若网格中最小正方形边长为1，求的面积；
(3)在直线上找一点，使得的值最大，并画出点的位置．
【变式2-3】（2022·天津市红桥区教师发展中心八年级期中）如图，已知三点A（-2，3），B（3，-3），C（-3，1），△ABC与△A1B1C1关于x轴对称，其中A1，B1，C1分别是点A，B，C的对应点．
(1)画出△A1B1C1，并写出三个顶点A1，B1，C1的坐标；
(2)若点是上一点，其关于轴的对称点为，求，的值．
【考点3 设计轴对轴图案】
【例3】（2022·江苏·八年级课时练习）如图所示的“钻石”型网格（由边长都为1个单位长度的等边三角形组成），其中已经涂黑了3个小三角形（阴影部分表示），请你再只涂黑一个小三角形，使它与阴影部分合起来所构成的图形是一个轴对称图形，一共有（ ）种涂法．
A．1B．2C．3D．4
【变式3-1】（2022·河北·九年级专题练习）如图为5×5的方格，其中有A、B、C三点，现有一点P在其它格点上，且A、B、C、P为轴对称图形，问共有几个这样的点P（ ）
A．5B．4C．3D．2
【变式3-2】（2022·全国·七年级专题练习）在3×3的正方形网格中，有三个小方格涂上阴影，请再在余下的6个空白的小方格中，选两个小方格并涂成阴影，使得图中的阴影部分组成一个轴对称图形，共有 ( )种不同的填涂方法．
A．3种B．4种C．5种D．6种
【变式3-3】（2022·江苏·八年级专题练习）现有如图1所示的两种瓷砖，请你从两种瓷砖中各选两块，拼成一个新的正方形，使拼成的图案为轴对称图形，如图2，要求：在图3，图4中各设计一种与示例拼法不同的轴对称图形．
【考点4 镜面对称】
【例4】（2022·江苏·宜兴外国语学校八年级阶段练习）小明在镜中看到身后墙上的时钟如下，你认为实际时间最接近9：00（ ）
A．B．C．D．
【变式4-1】（2022·全国·八年级专题练习）某公路急转弯处设立了一面圆形大镜子，从镜子中看到汽车车牌的部分号码如图所示，则该车牌照的部分号码为____．
【变式4-2】（2022·黑龙江·哈尔滨顺迈学校八年级阶段练习）从镜子中看到背后墙上电子钟的示意数为10：05,这时的实际时间为______.
【变式4-3】（2022·甘肃平凉·八年级期中）小明从平面镜子中看到镜中电子钟示数的像如图所示，这时的时刻应是________．
【考点5 利用轴对称求最值】
【例5】（2022·湖南·李达中学八年级阶段练习）如图，在Rt△ABC中，，AC＝6，BC＝8，AB＝10，AD是的平分线，若P，Q分别是AD何AC上的动点，则PC＋PQ的最小值是（ ）
A．2.4B．4C．4.8D．5
【变式5-1】（2022·河南驻马店·七年级期末）如图，四边形中，，，在、上分别找一点M、N，当周长最小时，则的度数为（ ）
A．B．C．D．
【变式5-2】（2022·全国·八年级专题练习）如图，在长方形ABCD中，AD＝BC＝3，AB＝CD＝4，AC＝5，动点M在线段AC上运动(不与端点重合)，点M关于边AD，DC的对称点分别为M1，M2，连接M1M2，点D在M1M2上，则在点M的运动过程中，线段M1M2长度的最小值是_______．
【变式5-3】（2022·福建龙岩·八年级期中）如图，在Rt△ABC中，∠A＝90°，AB＝8，AC＝6，BC＝10，M、N、P分别是边AB、AC、BC上的动点，连接PM、PN和MN，则PM+PN+MN的最小值是 _______．
【考点6 寻找构成等腰三角形的点的个数】
【例6】（2022·广东·丰顺县潘田中学九年级开学考试）如图，已知每个小方格的边长为，，两点都在小方格的顶点上，请在图中找一个顶点，使为等腰三角形，则这样的顶点有（ ）
A．个B．个C．个D．个
【变式6-1】（2022·安徽·合肥市第四十五中学八年级阶段练习）Rt△ABC中，∠ACB＝90°，∠A＝60°，在直线BC上取一点P使得△PAB是等腰三角形，则符合条件的点P有___个．
【变式6-2】（2022·安徽·利辛县汝集镇西关学校八年级期末）如图，的点在直线上，，若点P在直线上运动，当成为等腰三角形时，则度数是_______．
【变式6-3】（2022·天津市武清区杨村第五中学八年级期中）在平面直角坐标系中，点A，B的坐标分别是A（3，0），B（0，4），若点P在坐标轴上，且△PAB是等腰三角形，则满足条件的点P有_____个．
【考点7 利用三线合一求值】
【例7】（2022·河北保定·八年级期末）如图，一位同学拿了两块同样的含45°的三角尺，即等腰直角MNK，等腰直角ACB做了一个探究活动：将MNK的直角顶点M放在ABC的斜边AB的中点处，设AC＝BC＝a，猜想此时重叠部分四边形CEMF的面积为（ ）
A．a2B．a2C．a2D．a2
【变式7-1】（2022·广东·深圳市布心中学七年级期末）如图，△ACB和△DCE均为等腰直角三角形，且∠ACB=∠DCE=90°，点A、D、E中同一条直线上，CM平分∠DCE，连接BE，以下结论：①AD=DC；②CM⊥AE；③AE-BE=2CM；④∠BCM=∠CBE，正确的有（ ）
A．个B．个C．个D．个
【变式7-2】（2022·浙江·平阳苏步青学校八年级阶段练习）如图，CD是等腰三角形△ABC底边上的中线，BE平分∠ABC，交CD于点E，AC＝6，DE＝2，则△BCE的面积是( )
A．4B．6C．8D．12
【变式7-3】（2022·江苏·八年级单元测试）如图，在△ABC中，AB＝AC，AD⊥BC于点D，DE⊥AC于点E，CF⊥AB于点F，若DE＝4，则CF的长为_____.
【考点8 利用三线合一证明】
【例8】（2022·江苏·泰州市姜堰区第四中学八年级）已知：如图△ABC中，AB=AC，AD和BE是高，它们交于点H，且AE=BE．求证：
(1)△AHE≌△BCE；
(2)AH=2BD．
【变式8-1】（2022·全国·八年级专题练习）如图，△ABC中，AD是∠BAC的平分线，DE⊥AB，DF⊥AC，E、F为垂足，连接EF交AD于G，试判断AD与EF垂直吗？并说明理由．
【变式8-2】（2022·北京·垂杨柳中学八年级期中）如图，在△ABC中，AB＝AC，其中AD，BE都是△ABC的高．求证：∠BAD＝∠CAD＝∠EBC．
【变式8-3】（2022·山东青岛·七年级期末）已知，在中，，，平分交于点，点是边上的一动点（不与点重合），连接．
(1)如图①，若运动到上，过点作的垂线交于点，于点，于点，求证：；
(2)如图②，若运动到上，过点作的垂线与延长线交于点，延长交延长线于点，试猜想的数量关系并证明．
【考点9 利用等角对等边证明边长相等】
【例9】（2022·江苏·八年级单元测试）如图，已知△ABC中，AB＝6，AC＝8，∠ABC和∠ACB的平分线相交于点D，过点D作BC的平行线，分别交AB，AC于E，F，则△AEF的周长是_____.
【变式9-1】（2022·湖南长沙·八年级期中）如图，∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E，若BD＝9cm，DE＝4cm，求CE的长为__cm．
【变式9-2】（2022·浙江·乐清市知临寄宿学校八年级期中）如图，在△ABC中，∠BAC的平分线AD交BC于点D，E为AC上一点，AE＝AB，连接DE.
(1)求证：△ABD≌△AED；
(2)已知∠ABC＝2∠C且BD＝5，AB＝9，求AC长．
【变式9-3】（2022·福建·厦门双十中学八年级期末）如图，为的角平分线．
(1)如图1，若于点，交于点，，．则_______；
(2)如图2，于点，连接，若的面积是6，求的面积；
(3)如图3，若，，，则的长为_______．（用含的式子表示）
【考点10 利用等角对等边证明】
【例10】（2022·天津·八年级期中）如图：E在△ABC的AC边的延长线上，AB＝AC，D点在AB边上，DE交BC于点F，DF＝EF，求证：BD＝CE．
【变式10-1】（2022·浙江·八年级单元测试）如图，在中，AD平分，过点B作AD的垂线，垂足为点D，，交AB于点E，．

(1)求证：是等腰三角形；
(2)求证：．
【变式10-2】（2022·陕西西安·七年级期末）已知，小新在学习了角平分线的知识后，做了一个夹角为120°（即）的角尺来作的角平分线．
问题发现
(1)如图1，他先在边OA和OB上分别取，再移动角尺使，然后他就说射线OP是的角平分线．请问小新的观点是否正确，为什么？
问题探究
(2)如图2，小新在确认射线OP是的角平分线后，一时兴起，将角尺绕点P旋转了一定的角度，若角尺旋转后恰好使得，发现线段OD与OE有一定的数量关系．请你直接写出线段OD与OE的数量关系，并说明理由．
【变式10-3】（2022·江西·吉安县文博国际学校八年级开学考试）如图①，中，，、的平分线交于点，过点作EFBC交、于、．
(1)图①中有几个等腰三角形？猜想：与、之间有怎样的关系．
(2)如图②，若，其他条件不变，在第（1）问中与、间的关系还存在吗？
(3)如图③，若中的平分线与平分线交于，过点作OEBC，交于，交于．与、关系又如何？说明你的理由．
【考点11 作等腰三角形】
【例11】（2022·山东青岛·九年级专题练习）如图，已知：点P和直线BC．
求作：等腰直角三角形MPQ，是，点M落在BC上．
【变式11-1】（2022·福建省福州屏东中学八年级期中）我们知道，含有36°角的等腰三角形是特殊的三角形，通常把一个顶角等于36°的等腰三角形称为“黄金三角形”．在中，已知：，且，请用两种不同的尺规作图在上找点，使得是黄金三角形，并说明其中一种做法的理由．
【变式11-2】（2022·福建龙岩·八年级期末）如图，在中，，射线．
(1)在线段上取一点，使得，在射线上确定一点，使是以为底边的等腰三角形（尺规作图，保留作图痕迹，不写作法）；
(2)在（1）的条件下，连接，求证：．
【变式11-3】（2022·山东省青岛第六十三中学八年级期中）已知，线段，求作：等腰，使得顶角，上的高为．
【考点12 等边三角形的判定与性质】
【例12】（2022·全国·八年级期中）如图，在等边三角形ABC中，点D，E分别是BC，AB上的点，且BE＝CD，AD与CE相交于点F，连接BF，延长FE至G，使FG＝FA，若△ABF的面积为m，AF：EF＝5：3，则△AEG的面积是（ ）
A．B．C．D．
【变式12-1】（2022·河南·郑州市第四初级中学八年级期中）如图，边长为a的等边△ABC中，BF是AC上中线且BF＝2b，点D在BF上，连接AD，在AD的右侧作等边△ADE，连接EF，则△AEF周长的最小值是（ ）
A．B．C．D．
【变式12-2】（2022·广东·东华学校八年级期中）如图，已知△ABC和△CDE均是等边三角形，点B、C、E在同一条直线上，AE与BD交于点O，AE与CD交于点G，AC与BD交于点F，连接OC、FG，
(1)求证：BD=AE，并求出∠DOE的度数；
(2)判断△CFG的形状并说明理由；
(3)求证：OA+OC=OB．
【变式12-3】（2022·广东·汕头市金平区金园实验中学八年级期末）晓芳利用两张正三角形纸片，进行了如下探究：
初步发现：如图1，△ABC和△DCE均为等边三角形，连接AE交BD延长线于点F，求证：∠AFB＝60°；
深入探究：如图2，在正三角形纸片△ABC的BC边上取一点D，作∠ADE＝60°交∠ACB外角平分线于点E，探究CE，DC和AC的数量关系，并证明；
拓展创新：如图3，△ABC和△DCE均为正三角形，连接AE交BD于P，当B，C，E三点共线时，连接PC，若BC＝3CE，直接写出下列两式分别是否为定值，并任选其中一个进行证明：
（1）；
（2）．
【考点13 含30度的直角三角形】
【例13】（2022·广东·丰顺县球山中学九年级开学考试）如图，在 中，，， 在 内部， 平分 ，，若 ，，则 的长为____．
【变式13-1】（2022·福建省永春崇贤中学九年级阶段练习）如图，将△ABC绕点B逆时针旋转得到△DBE，且点E落在AB上，DE的延长线与AC相交于点F，连接DA，BF，若，．
(1)求证△ADF≌△BDF；
(2)若，求DF的长．
【变式13-2】（2022·福建省长乐第七中学八年级阶段练习）已知∠ABC＝60°，AB＝BC，D是BC边上一点，延长AD到点E，使得AD＝DE，连接CE，过点D作BC的垂线，交CE的垂直平分线于点F，连接EF．
(1)如图1，当点D与点C重合时，证明：BF＝2DF；
(2)如图2，当点D不与B，C两点重合时，（1）中的结论是否还成立？并说明理由．
【变式13-3】（2022·福建·莆田哲理中学八年级期末）如图1，在△ABD中，点E，F分别是AB和AD上的点，满足AE=EF，连接EF并延长交BD延长线于点C．
(1)若DC=DF=EF，求证：AB=BC；
(2)如图2，过B作BG⊥AD，垂足为G．
（i）求证：∠ABG=∠GBD+∠C；
（ii）如图3，连接AC，若∠GBD=30°，AF=BD，△BDG的面积为4，求△AFC的面积．
【考点14 尺规作垂直平分线或垂线】
【例14】（2022·陕西省西安爱知中学八年级阶段练习）如图，已知，P为边上一点，请用尺规作图的方法在边上求作一点E，使．（保留作图痕迹，不写作法）
【变式14-1】（2022·重庆市第十一中学校七年级阶段练习）如图，已知和线段m，请用尺规完成如下作图（保留作图痕迹，不写作法）．
(1)求作，使；
(2)作出（1）中的三条高．
【变式14-2】（2022·广东广州·八年级期中）如图，在钝角△ABC中．
(1)用尺规作图法作AC的垂直平分线，与边BC、AC分别交于点D、E（保留作图痕迹，不用写作法）；
(2)在（1）的条件下，画出△ABC的AC边上的高BH（可用三角板画图），连接AD，直接写出∠ADE和∠HBC的大小关系．
【变式14-3】（2022·江苏·八年级阶段练习）小宇遇到了这样一个问题：
已知：如图，，点A，B分别在射线OM，ON上，且满足．
求作：线段OB上的一点C，使的周长等于线段的长．
以下是小宇分析和求解的过程，请补充完整：首先画草图进行分析，如图1所示，若符合题意得点C已经找到，即得周长等于OB的长，那么由，可以得到 ．
对于这个式子，可以考虑用截长得办法，在BC上取一点D，使得，那么就可以得到 ．
若连接AD，由 ．（填推理依据）．可知点C在线段AD得垂直平分线上，于是问题得解法就找到了．
请根据小宇得分析，在图2中完成作图（尺规作图，不写做法，保留作图痕迹）．
【考点15 垂直平分线的判定与性质】
【例15】（2022·广东·广州市第九十七中学八年级期中）已知在△ABC中，∠CAB的平分线AD与BC的垂直平分线DE交于点D，DM⊥AB于M，DN⊥AC的延长线于N．
（1）证明：BM=CN；
（2）当∠BAC=70°时，求∠DCB的度数．
【变式15-1】（2022·全国·八年级课时练习）如图，△ABC中，BE平分∠ABC，E在AC垂直平分线上，EF⊥BC于F，EG⊥AB于G，
求证： （1）AG＝CF；
（2）BC﹣AB＝2FC．
【变式15-2】（2022·山西临汾·八年级阶段练习）情景一：小明在数学兴趣小组探究活动课上发现：对于一个△ABC，分别作边AB，AC的垂直平分线DM，EN相交于点O，如图1所示，此时经过测量后，得到∠MAN＝30°，根据上述条件，能不能得到∠BAC的度数呢？小明结合所学过的知识进行了以下论证．
证明：∵DM是边AB的垂直平分线，
∴MA＝MB，
∴∠MAB＝∠B．
同理可得∠NAC＝∠C，
则
解得∠BAC＝105°．
情景二：小明继续对上述问题进行探究发现：若边AB，AC的垂直平分线DM，EN相交于点O，如图2所示，试判断∠MAN与∠BAC之间的数量关系．
(1)情景一中得到∠MAB＝∠B的理由是______．
(2)在图1的情况下，若∠MAN的度数为α，则∠BAC的大小为______（用含α的代数式表示）．
(3)请写出情景二中∠MAN与∠BAC之间的数量关系，并说明理由．
【变式15-3】（2022·江苏·八年级专题练习）如图，在△ABC中，CA＝CB，过点A作射线AP∥BC，点M、N分别在边BC、AC上（点M、N不与所在线段端点重合），且BM＝AN，连结BN并延长交射线AP于点D，连结MA并延长交AD的垂直平分线于点E，连结ED．
【猜想】如图①，当∠C＝30°时，可证△BCN≌△ACM，从而得出∠CBN＝∠CAM，进而得出∠BDE的大小为______度．
【探究】如图②，若∠C＝β．
（1）求证：△BCN≌△ACM．
（2）∠BDE的大小为______度（用含β的代数式表示）．
【应用】如图③，当∠C＝120°时，AM平分∠BAC，若AM、BN交于点F，DE＝DF，DE＝1，则△DEF的面积为______．
【考点16 等腰三角形中的新定义问题】
【例16】（2022·山西临汾·八年级阶段练习）综合实践
在学习全等三角形的知识时，数学兴趣小组发现这样一个模型：它是由两个共顶点且顶角相等的等腰三角形构成的，在相对位置变化的同时，始终存在一对全等三角形．兴趣小组成员经过研讨给出定义：如果两个等腰三角形的顶角相等，且顶角的顶点互相重合，则称此图形为“手拉手全等模型”．因为顶点相连的四条边，可以形象地看作两双手，所以通常称为“手拉手模型”．如图1，与都是等腰三角形，其中，则．
(1)【初步把握】如图2，与都是等腰三角形，，，且，则有_______________．
(2)【深入研究】如图3，已知，以为边分别向外作等边和等边，并连接BE，，求证：．
(3)【拓展延伸】如图4，在两个等腰直角三角形和中，，，，连接，，交于点P，请判断和的关系，并说明理由．
【变式16-1】（2022·福建厦门·八年级期末）定义：一个三角形，若过一个顶点的线段将这个三角形分为两个三角形，其中一个是直角三角形，另一个是等腰三角形，则称这个三角形是等直三角形，这条线段叫做这个三角形的等直分割线段．
例如：
如图，在中，
∵于D，且，
∴是直角三角形，是等腰三角形，
∴是等直三角形，
AD是的一条等直分割线段．
(1)如图，已知中，，DE是AB的垂直平分线，请说明AD是的一条等直分割线段．
(2)若是一个等直三角形，恰好有两条等直分割线，和均小于45°，求证：是等腰三角形．
【变式16-2】（2022·浙江·八年级单元测试）新定义：顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”．
(1)如图1，和互为“兄弟三角形”，点A为重合的顶角顶点．求证：．
(2)如图2，和互为“兄弟三角形”，点A为重合的顶角顶点，点D、E均在外，连接BD、CE交于点M，连接AM，求证：AM平分．
【变式16-3】（2022·河南省直辖县级单位·八年级期末）阅读下列材料，解答问题：
定义：线段BM把等腰△ABC分成△ABM与△BCM（如图1），如果△ABM与△BCM均为等腰三角形，那么线段BM叫做△ABC的完美分割线．
(1)如图1，已知△ABC中，，BM为△ABC的完美分割线，且，则 °， °；
(2)如图2，已知△ABC中，，求证：AN为△ABC的完美分割线；
(3)如图3，已知△ABC是一等腰三角形纸片，AB＝AC，AN是它的一条完美分割线，且，将△ACN沿直线AN折叠后，点C落在点处，交BN于点M．求证：．
【考点17 尺规作图作角平分线】
【例17】（2022·四川广元·中考真题）观察下列作图痕迹，所作线段为的角平分线的是（ ）
A．B．
C．D．
【变式17-1】（2022·江苏·八年级专题练习）利用作角平分线的方法，可以把一个已知角（ ）
A．三等分B．四等分C．五等分D．六等分
【变式17-2】（2022·四川天府新区教育科学研究院附属中学八年级阶段练习）如图，在Rt△ABC中，∠C=90°，首先以顶点B为圆心，适当长为半径作弧，在边BC、BA上截取BE、BD；然后分别以点D、E为圆心，大于为半径作弧，两弧在∠CBA内交于点F；作射线BF交AC于点G．若CG=4，P为边AB上一动点，则GP的最小值为（ ）
A．2B．4C．8D．无法确定
【变式17-3】（2022·广西北海·八年级期中）如图，在中，，点D在AB的延长线上．
(1)利用尺规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）；
①作的平分线BM；
②作边BC上的中线AE，并延长AE交BM于点F；
(2)在（1）的前提下，猜测BF与边AC的位置关系，并写出证明过程．
【考点18 角平分线的判定与性质的综合求值】
【例18】（2022·广东汕头·八年级期末）如图，的三边，，长分别是，，，其三条角平分线将分为三个三角形，则：：等于（ ）
A．：：B．：：
C．：：D．：：
【变式18-1】（2022·全国·八年级课时练习）如图，在四边形ABCD中，AB∥CD，∠B＝90°，∠DAB与∠ADC的平分线相交于BC边上的M点，则下列结论：①∠AMD＝90°；②点M为BC的中点；③AB+CD＝AD；④△ADM的面积是梯形ABCD面积的一半．其中正确的个数有（ ）
A．1个B．2个C．3个D．4个
【变式18-2】（2022·重庆江北·八年级期末）如图，已知和都是等腰三角形，，、交于点，连接．下列结论：①；②⊥；③平分；④．其中正确结论的是__________．
【变式18-3】（2022·全国·八年级课时练习）如图1，在△ABC中，∠BAC的平分线AD与∠BCA的平分线CE交于点O．
(1)求证：∠AOC＝90°＋∠ABC；
(2)当∠ABC＝90°时，且AO＝3OD（如图2），判断线段AE，CD，AC之间的数量关系，并加以证明．
【考点19 角平分线的判定与性质的综合证明】
【例19】（2022·全国·八年级专题练习）已知：如图1，在中，，，，是角平分线，与相交于点，，，垂足分别为，．
【思考说理】
（1）求证：．
【反思提升】
（2）爱思考的小强尝试将【问题背景】中的条件“”去掉，其他条件不变，观察发现（1）中结论（即）仍成立．你认为小强的发现正确吗？如果不正确请举例说明，如果正确请仅就图2给出证明．
【变式19-1】（2022·全国·八年级课时练习）如图，已知，AE，BD是的角平分线，且交于点P．
（1）求的度数．
（2）求证：点在的平分线上．
（3）求证：①；
②．
【变式19-2】（2022·四川成都·七年级期末）如图，在和中，，，，．连接，交于点O．
(1)求证：；
(2)求的度数：
(3)小明同学对该题进行了进一步研究，他连接了，并提出了下面结论：平分．请给予证明．
【变式19-3】（2022·山东·北辛中学八年级阶段练习）（1）如图①，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形．请你参考这个作全等三角形的方法，解答下列问题：
（2）如图②，在△ABC中，∠ACB是直角，∠B＝60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．请你判断并写出FE与FD之间的数量关系；并证明．
（3）如图③，在△ABC中，∠B＝60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F，请问，你在（2）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．
【考点20 角平分线的实际应用】
【例20】（2022·江苏·八年级专题练习）如图，三条公路两两相交，现计划在△ABC中内部修建一个探照灯，要求探照灯的位置到这三条公路的距离都相等，则探照灯位置是△ABC（ ）的交点．
A．三条角平分线B．三条中线
C．三条高的交点D．三条垂直平分线
【变式20-1】（2022·江苏·八年级单元测试）如图，要在河流的右侧、公路的左侧M区建一个工厂，位置的选择要满足到河流和公路的距离相等，小红说工厂应该建在河流与公路夹角的平分线上，请你帮小红说出她的理由__________________________________________________．
【变式20-2】（2022·全国·八年级）如图，l3与两条平行公路l1，l2三条公路相交，若要在l1上确定某个位置，使其到另两条公路的距离相等，这样的位置有（ ）
A．1个B．2个C．3个D．无数个
【变式20-3】（2022·黑龙江黑河·八年级期末）如图，直线，，表示三条公路．现要建造一个中转站P，使P到三条公路的距离都相等，则中转站P可选择的点有（ ）
A．一处B．二处C．三处D．四处