苏科版数学八上期末专题复习专题05 翻折变换精选（2份，原卷版+解析版）

这是一份苏科版数学八上期末专题复习专题05 翻折变换精选（2份，原卷版+解析版），文件包含苏科版数学八上期末专题复习专题05翻折变换精选原卷版doc、苏科版数学八上期末专题复习专题05翻折变换精选解析版doc等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。

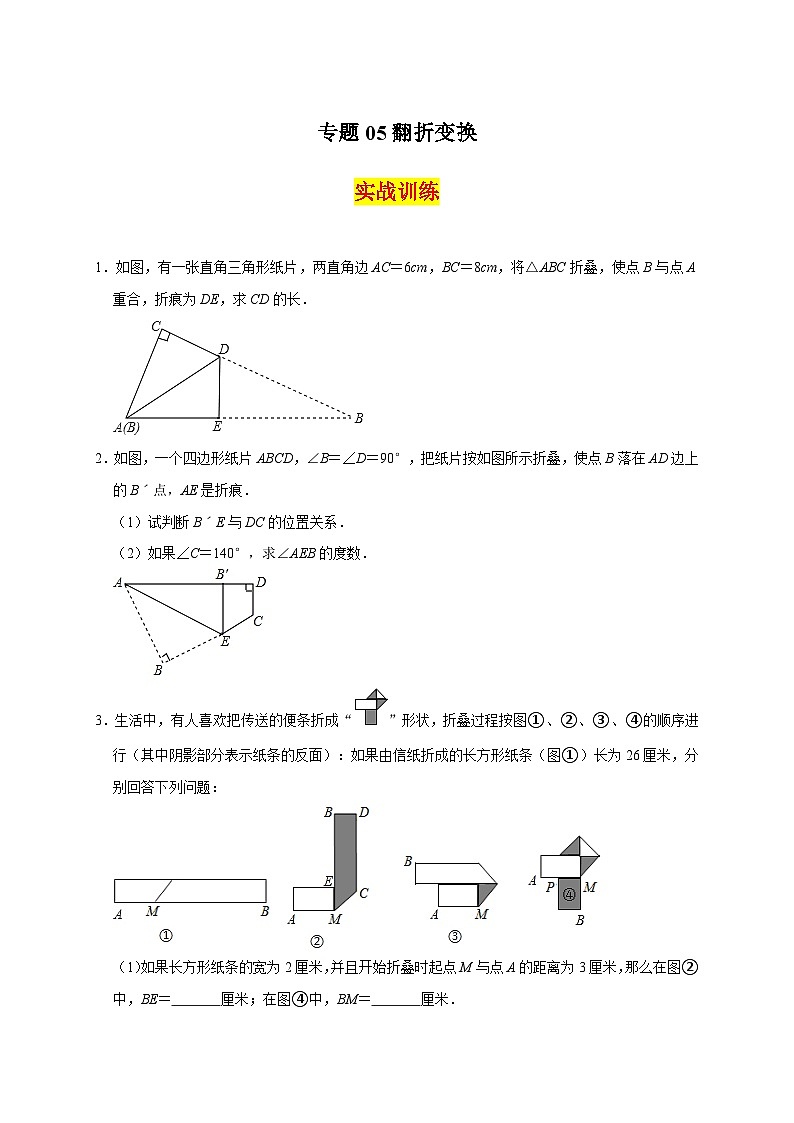
1．如图，有一张直角三角形纸片，两直角边AC＝6cm，BC＝8cm，将△ABC折叠，使点B与点A重合，折痕为DE，求CD的长．
2．如图，一个四边形纸片ABCD，∠B＝∠D＝90°，把纸片按如图所示折叠，使点B落在AD边上的Bˊ点，AE是折痕．
（1）试判断BˊE与DC的位置关系．
（2）如果∠C＝140°，求∠AEB的度数．
3．生活中，有人喜欢把传送的便条折成“”形状，折叠过程按图①、②、③、④的顺序进行（其中阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为26厘米，分别回答下列问题：
（1）如果长方形纸条的宽为2厘米，并且开始折叠时起点M与点A的距离为3厘米，那么在图②中，BE＝ 厘米；在图④中，BM＝ 厘米．
（2）如果长方形纸条的宽为x厘米，现不但要折成图④的形状，而且为了美观，希望纸条两端超出点P的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点M与点A的距离（结果用x表示）．
4．如图，折叠长方形的一边AD，使点D落在边BC的点F处，已知AB＝8cm，BC＝10cm，求；
（1）线段BF的长；
（2）线段EC的长．
5．如图，在矩形ABCD中，AB＝5，BC＝7，点E是AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A′恰好落在∠BCD 的平分线上时，CA′的长为多少？
6．在数学实验课上，李静同学剪了两张直角三角形纸片，进行了如下的操作：
操作一：如图1，将Rt△ABC纸片沿某条直线折叠，使斜边两个端点A与B重合，折痕为DE．
（1）如果AC＝5cm，BC＝7cm，可得△ACD的周长为 ；
（2）如果∠CAD：∠BAD＝1：2，可得∠B的度数为 ；
操作二：如图2，李静拿出另一张Rt△ABC纸片，将直角边AC沿直线CD折叠，使点A与点E重合，若AB＝10cm，BC＝8cm，请求出BE的长．
7．如图，在矩形纸片ABCD中，AB＝6，BC＝8将矩形纸片ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，连接AE．
（1）证明：BF＝DF；
（2）求AF的值；
（3）求△DBF的面积．
8．如图，在长方形ABCD中，AB＝6，AD＝8，E、F分别是BC、CD上的一点，EF⊥AE，将△ECF沿EF翻折得到ΔEC′F，连接AC′．若△AEC′是等腰三角形，且AE＝AC′，则BE＝ ．
9．如图①所示，在三角形纸片ABC中，∠C＝70°，∠B＝65°，将纸片的一角折叠，使点A落在△ABC内的点A'处．
（1）若∠1＝40°，∠2＝ ．
（2）如图①，若各个角度不确定，试猜想∠1，∠2，∠A之间的数量关系，直接写出结论．
②当点A落在四边形BCDE外部时（如图②），（1）中的猜想是否仍然成立？若成立，请说明理由，若不成立，∠A，∠1，∠2之间又存在什么关系？请说明．
（3）应用：如图③：把一个三角形的三个角向内折叠之后，且三个顶点不重合，那么图中的∠1+∠2+∠3+∠4+∠5+∠6和是 ．
10．如图所示，有一块直角三角形纸片，∠C＝90°，AB＝5cm，BC＝3cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CD的长为（ ）
A．1cmB．cmC．1.5cmD．cm
11．如图，在Rt△ABC中，∠B＝90°，AB＝8，BC＝6，延长BC至E，使得CE＝BC，将△ABC沿AC翻折，使点B落点D处，连接DE，则DE的长为（ ）
A．B．C．D．
12．如图，在Rt△ABC中，∠ACB＝90°，BC＝6，点D为斜边AB上的一点，连接CD，将△BCD沿CD翻折，使点B落在点E处，点F为直角边AC上一点，连接DF，将△ADF沿DF翻折，点A恰好与点E重合．若DC＝5，则AF＝ ．
13．如图，△ABC中，AB＝12，AC＝16，BC＝20．将△ABC沿射线BM折叠，使点A与BC边上的点D重合，E为射线BM上一个动点，当△CDE周长最小时，CE的长为 ．
14．如图，将边长为8cm的正方形纸片ABCD折叠，使点D落在BC边中点E处，点A落在点F处，折痕为MN，则线段CN的长度为 ．
15．长方形纸片ABCD的边AB＝6cm，AD＝10cm，将纸片沿着AC折叠，点D落在点D'处，且AD'与BC交于点E，求BE的长．
16．已知：如图，在Rt△ABC中，∠C＝90°，沿过B点的一条直线BE折叠这个三角形，使C点与AB边上的一点D重合．点D恰为AB的中点，DE＝2，求△ABC的周长．
17．如图，把长方形ABCD沿AC折叠，AD落在AD′处，AD′交BC于点E，已知AB＝2cm，BC＝4cm．（长方形的对边相等，四个角都为直角）
（1）求证：AE＝EC；
（2）求EC的长；
（3）求重叠部分的面积．
18．如图，有一块直角三角形纸片，∠C＝90°，AC＝4cm，BC＝3cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为 ．
19．如图，在Rt△ABC中，∠C＝90°，沿过点A的一条直线AE折叠Rt△ABC，使点C恰好落在AB边的中点D处，则∠B的度数是 ．
20．如图，折叠等腰三角形纸片ABC，使点C落在边AB上的点F处，折痕为DE．已知AB＝AC，FD⊥BC．
（1）求证：∠AFE＝90°；
（2）如果AF＝3，BF＝6，求AE的长．
21．如图，在△ABC中，∠C＝90°，AC＝5cm，BC＝12cm，将△ABC沿过A点的直线折叠，使点C落在AB边上的点D处，折痕与BC交于点E．
（1）试用尺规作图作出折痕AE；（要求：保留作图痕迹，不写作法．）
（2）连接DE，求线段DE的长度．
22．如图，长方形ABCD的纸片，长AD＝10厘米，宽AB＝8厘米，AD沿点A对折，点D正好落在BC上的点F处，AE是折痕．
（1）图中有全等的三角形吗？如果有，请直接写出来；
（2）求线段BF的长；
（3）求线段EF的长．
23．如图，把△ABC纸片沿DE折叠，当点C落在四边形ABDE的外部时，此时测得∠1＝106°，∠C＝35°，求∠2的度数．
24．如图，△ABC中，∠BAC＝90°，AB＝3，AC＝4，点D是BC的中点，将△ABD沿AD翻折得到△AED，连CE，则线段CE的长等于（ ）
A．2B．C．D．
25．如图，点D为△ABC边AB的中点，将△ABC沿经过点D的直线折叠，使点A刚好落在BC边上的点F处，若∠B＝44°，则∠BDF的度数为（ ）
A．86°B．88°C．90°D．92°
26．如图，Rt△ABC，∠ACB＝90°，AC＝3，BC＝4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为 ．
27．已知：如图，将矩形纸片ABCD沿对角线BD对折，点C落在点E的位置，AD与BE相交于点F．
（1）求证：△BDF是等腰三角形；
（2）若AB＝8，AD＝10，求BF的长．
28．在△ABC中，∠B，∠C均为锐角且不相等，线段AD，AE分别是△ABC中BC边上的高和△ABC的角平分线．
（1）如图1，∠B＝70°，∠C＝30°，求∠DAE的度数．
（2）若∠B＝α，∠DAE＝10°，则∠C＝
（3）F是射线AE上一动点，G、H分别为线段AB，BE上的点（不与端点重合），将△ABC沿着GH折叠，使点B落到点F处，如图2所示，其中∠1＝∠AGF，∠2＝∠EHF，请直接写出∠1，∠2与∠B的数量关系．
29．如图，点A、B、C、O在网格中小正方形的顶点处，直线l经过点C、O，将△ABC沿l平移得到△MNO，M是A的对应点，再将这两个三角形沿l翻折，P、Q分别是M、A的对应点．已知网格中每个小正方形的边长都等于1，则PQ2的值为 ．
30．如图，有一块直角三角形纸片，两直角边AC＝6cm，BC＝8cm，现将纸片折叠，使点B落在点A上，折痕为DE，则CD的长为 cm．