2024-2025学年江苏省连云港市新海初级中学八年级（上）期中考试数学试卷（含答案）

这是一份2024-2025学年江苏省连云港市新海初级中学八年级（上）期中考试数学试卷（含答案），共15页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
一、选择题：本题共8小题，每小题3分，共24分。在每小题给出的选项中，只有一项是符合题目要求的。
1.汉字是世界上最古老的文字之一，它是中华文明的符号与象征，许多中国汉字的形体和结构充满着“对称美”，下列四个汉字中，可以看作是轴对称图形的是( )
A. B. C. D.
2.下列各组线段能构成直角三角形的一组是( )
A. 1，4，4B. 1，2，3C. 3，4，5D. 4，5，6
3.下列说法正确的是( )
A. 9的平方根是3B. −9的平方根是−3
C. −22没有平方根D. 2是4的一个平方根
4.如图，在▵ABC中，∠ACB=90∘，DE垂直平分AB交BC于点D，若▵ACD的周长为50cm，则AC+BC=( )
A. 25cmB. 45cmC. 50cmD. 55cm
5.如图，若∠BAC=∠BAD，∠ABC=∠ABD，则直接判定▵ABC≌▵ABD的理由是( )
A. SASB. SSSC. ASAD. AAS
6.如图，已知OC平分∠AOB，CD//OB，若OD=4，则CD的长为( )
A. 4B. 5C. 3D. 2
7.如图，在Rt▵ABC中，∠C=90∘，AF是角平分线，AB=8，CF=32，则▵AFB的面积为( )
A. 6B. 154C. 152D. 132
8.如图所示，边长为2的等边三角形ABC中，D点在边BC上运动(不与B、C重合)，点E在边AB的延长线上，点F在边AC的延长线上，AD=DE=DF.点D在BC边上从B至C的运动过程中，▵BED周长变化规律为( )
A. 不变B. 一直变小C. 先变大后变小D. 先变小后变大
二、填空题：本题共8小题，每小题3分，共24分。
9.计算 36的结果为 ．
10.如图是从镜子里看到的号码，则实际号码应是 ．
11.等腰三角形的两边分别长6cm和13cm，则它的周长是 ．
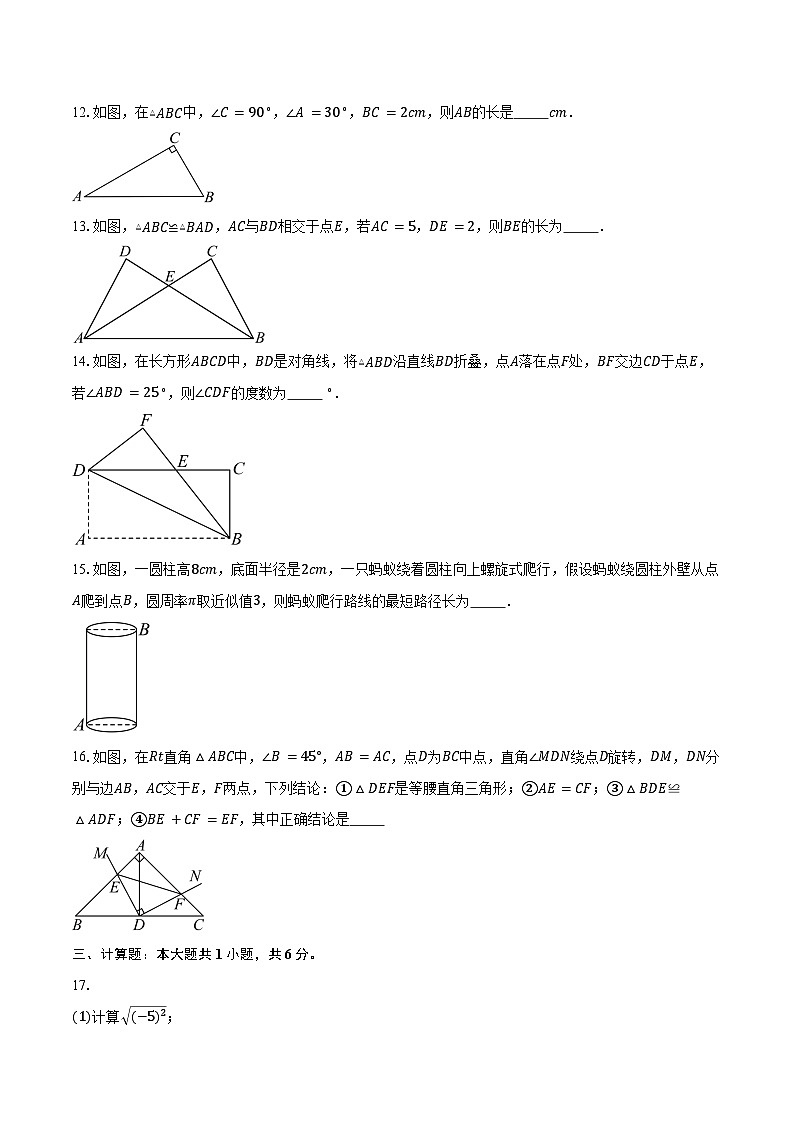
12.如图，在▵ABC中，∠C=90∘，∠A=30∘，BC=2cm，则AB的长是 cm．
13.如图，▵ABC≌▵BAD，AC与BD相交于点E，若AC=5，DE=2，则BE的长为 ．
14.如图，在长方形ABCD中，BD是对角线，将▵ABD沿直线BD折叠，点A落在点F处，BF交边CD于点E，若∠ABD=25∘，则∠CDF的度数为 ∘．
15.如图，一圆柱高8cm，底面半径是2cm，一只蚂蚁绕着圆柱向上螺旋式爬行，假设蚂蚁绕圆柱外壁从点A爬到点B，圆周率π取近似值3，则蚂蚁爬行路线的最短路径长为 ．
16.如图，在Rt直角△ABC中，∠B=45°，AB=AC，点D为BC中点，直角∠MDN绕点D旋转，DM，DN分别与边AB，AC交于E，F两点，下列结论：①△DEF是等腰直角三角形；②AE=CF；③△BDE≌△ADF；④BE+CF=EF，其中正确结论是
三、计算题：本大题共1小题，共6分。
17.
(1)计算 (−5)2；
(2)求式中x的值．x2−64=0．
四、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题8分)
已知2b+3的平方根为±3，3a+b的算术平方根为6．
(1)求a，b的值；
(2)求4a−6b的平方根．
19.(本小题8分)
△ABC在平面直角坐标系中的位置如图所示．
(1)画出△ABC关于y轴的对称图形△DEF(点A，B，C分别与点D，E，F对应)，并直接写出D，E，F三点的坐标；
(2)连接CF、CD，则△DFC的面积为_ _.
20.(本小题8分)
如图，在Rt▵ABC中，∠ACB=90∘，AC=12，点F是AC边上一点，CF=5.用直尺和圆规按要求作图(不写作法，保留作图痕迹)，并回答问题：
(1)在边AB上作点D，使得点D到边CA、CB的距离相等；
(2)在射线CD上作点E，使得点E到点A、点C的距离相等；
(3)若点P是射线CD上一个动点，当FP+AP取最小值时，在图中作出符合要求的点P，FP+AP的最小值是 ．
21.(本小题8分)
如图，∠ACB=90∘，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E，AD=2.5cm，DE=1.7cm．
(1)证明：▵ACD≌▵CBE；
(2)求BE的长．
22.(本小题8分)
某工厂的大门如图所示，其中下方是高为2.3米、宽为2米的矩形，上方是半径为1米的半圆形．货车司机小王开着一辆高为3.0米，宽为1.6米的装满货物的卡车，能否进入如图所示的工厂大门？请说明你的理由．
23.(本小题8分)
如图，在▵ABC中，点D在边AC上，连接BD，DB=BC，E是CD的中点，F是AB的中点，连接EF，求证：EF=12AB．
24.(本小题8分)
我国是最早了解勾股定理的国家之一，汉代数学家赵爽为了证明勾股定理，创制了一幅如图1所示“赵爽弦图”(边长为c的大正方形中放四个全等的直角三角形，两直角边长分别为a，b，斜边长为c).
(1)如图1，请用两种不同方法表示图中阴影部分面积．
方法1：S阴影= ；
方法2：S阴影= ；
根据以上信息，可以得到等式： ；
(2)小亮将“弦图”中的4个三角形进行了运动变换，得到图2，请利用图2证明勾股定理；
(3)如图3，将图2的2个三角形进行了运动变换，若a=6，b=3，求阴影部分的面积．
25.(本小题8分)
如图，已知▵ABC中，∠B=90∘，AB=8cm，BC=6cm，P，Q是▵ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，当点Q运动到点A时运动结束，设出发的时间为t秒．
(1)出发2秒时，求PQ的长；
(2)当点Q在边BC上运动时，通过计算说明PQ能否把▵ABC的周长平分；
(3)当点Q在边CA上运动时，求能使▵BCQ成为等腰三角形的运动时间．
26.(本小题8分)
我们知道：过三角形的顶点引一条直线，可以将它分成两个小三角形．如果每个小三角形都有两个相等的内角，则我们称这条直线为原三角形的“美丽线”.如下图，直线CD为▵ABC的“美丽线．
(1)如下图，在▵ABC中，∠A=90∘，∠C=35∘，请利用直尺和量角器在图2中画出▵ABC的“美丽线”(标出所得三角形的内角度数，不要求写画法)．
(2)在▵ABC中，∠A=α，∠B=βα≤β.若▵ABC存在过点C的“美丽线”，试探究α与β的关系，
下面是对这个问题的部分探究过程：
设CD为▵ABC的“美丽线”，点D在边AB上，则▵BCD中各两个相等的内角．
[探究1]
如下图，当∠ACD=∠ADC时，因为∠A=α，所以∠ADC= ，且∠ADC为锐角，则∠CDB为钝角，所以▵CDB中，∠DCB=∠B=β，由此可以得到，α与β关系为 其中α的取值范围 ．
(3) [探究2]
借助下面的图形，请你继续完成本问题的探究，直接写出α与β的关系．
参考答案
1.A
2.C
3.D
4.C
5.C
6.A
7.A
8.D
9.6
10.3265
11.32cm
12.4
13.3
14.40
15.10cm
16.①②③
17.【小题1】
解： (−5)2= 25=5；
【小题2】
x2−64=0，
x2=64，
x=±8．

18.【小题1】
解：∵2b+3的平方根为±3，
∴2b+3=9，解得：b=3，
∵3a+b的算术平方根为6，
∴3a+b=36，
∵b=3，
∴a=11．
【小题2】
∵a=11，b=3，
∴4a−6b=4×11−6×3=44−18=26，
则4a−6b的平方根为± 26．

19.【小题1】
解：如图所示，△DEF即为所求，D(−4,6)、E(−5,2)、F(−2,1)．
【小题2】
10

20.【小题1】
解：点D如图所示：
【小题2】
解：点E如图所示：
【小题3】
解：点P如图所示：
∵CF=5，
∴CF′=5，
即在Rt▵ACF′中，AC2+CF′2=AF′2，
即122+52=169=132，
即FP+AP=F′P+AP=AF′=13．

21.【小题1】
证明：∵AD⊥CE，BE⊥CE，
∴∠ADC=∠CEB=90∘，∠BCE+∠EBC=90∘，
∵∠ACB=90∘，
∴∠BCE+∠DCA=90∘，
∵∠BCE+∠EBC=90∘，
∴∠DCA=∠EBC，
∵AC=BC，
∴▵ACD≌▵CBEAAS；
【小题2】
解：∵▵ACD≌▵CBEAAS，
∴BE=CD，AD=CE，
∵AD=2.5cm，DE=1.7cm，
∴BE=CD=CE−DE=AD−DE=0.8cm，
故答案为：0.8cm．

22.解：这辆货车不能通过这个大门，理由如下：
如图，设BB′与矩形的宽的交点为E，

∵AB=1m,AE=1.62=0.8m,∠AEB=90∘，
∴BE= AB2−AE2= 12+0.82=0.6m，
∴BB′=BE+EB′=2.3+0.6=2.9m