2024-2025学年江苏省连云港新海初级中学七年级（上）期中考试数学试卷（含答案）

这是一份2024-2025学年江苏省连云港新海初级中学七年级（上）期中考试数学试卷（含答案），共10页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
一、选择题：本题共8小题，每小题3分，共24分。在每小题给出的选项中，只有一项是符合题目要求的。
1.−12024的相反数是( )
A. 12024B. −12024C. 2024D. −2024
2.下列数0.3030830003…(每两个3之间多一个0)，3.1415926，2π，0.625(625循环)中有理数的个数有( )
A. 1个B. 2个C. 3个D. 4个
3.下面计算正确的是( )
A. a2+a2=a4B. a+2a2=3a2
C. −a+b=−a+bD. 2a−b=2a−2b
4.下面各组数中，相等的一组是( )
A. −33与−33B. 233与233C. −−2与−−2D. −2与−22
5.下列说法错误的是( )
A. 代数式m+5，mb，−2都是整式B. 单项式−ab的系数是−1，次数是1
C. 多项式3x−π的项是3x，−πD. 多项式5x2y−2xy+4x是三次三项式
6.某口罩经销商将一批口罩以每盒60元的价格出售，每周可销售80盒．现准备提价销售，经市场调研发现：每盒每提价2元，每周销售量就会减少6盒．若口罩每盘售价xx>60元，则销量为( )盒．
A. 80−6×x2B. 80−6x−60C. 80−6×60−x2D. 80−6×x−602
7.烷烃是一类由碳、氢元素组成的有机化合物，在生产生活中可作为燃料、润滑剂等原料，也可用于动、植物的养护.通常用碳原子的个数命名为甲烷、乙烷、丙烷、⋯、癸烷(当碳原子数目超过10个时即用汉文数字表示，如十一烷、十二烷…)等，甲烷的化学式为CH4，乙烷的化学式为C2H6，丙烷的化学式为C3H8…，其分子结构模型如图所示，按照此规律，十二烷的化学式为( )
A. C12H24B. C12H25C. C12H26D. C12H21
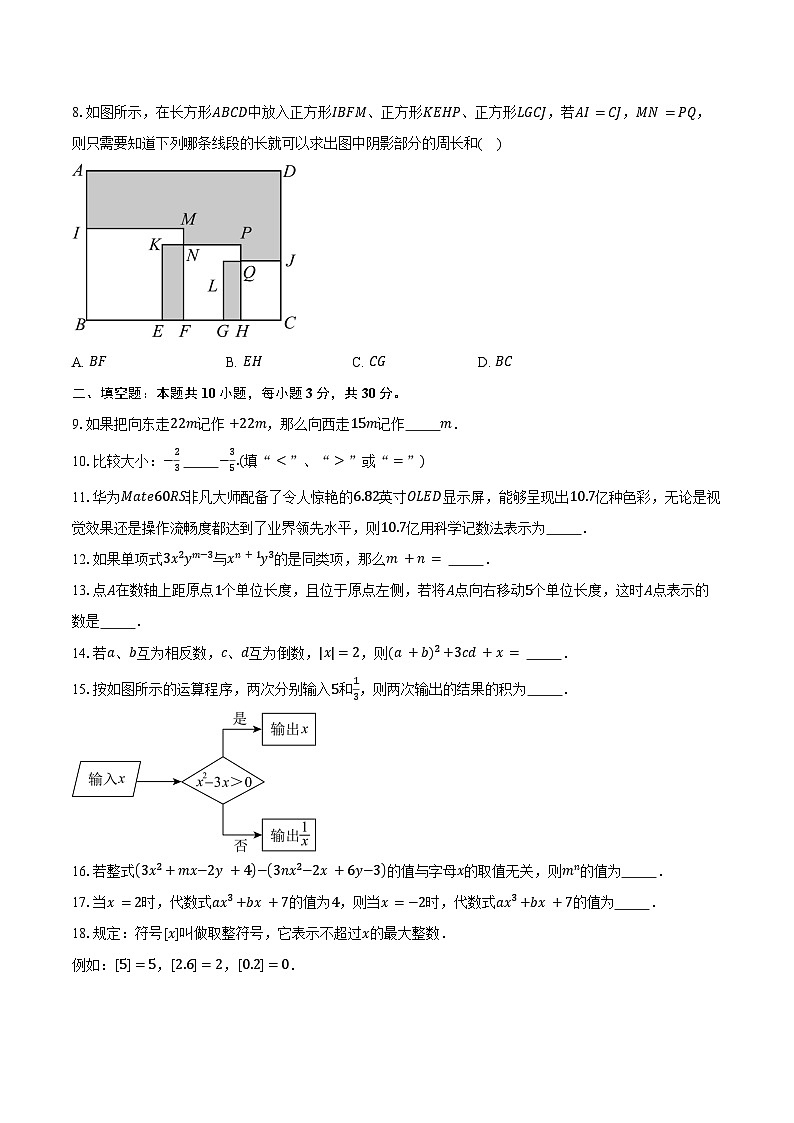
8.如图所示，在长方形ABCD中放入正方形IBFM、正方形KEHP、正方形LGCJ，若AI=CJ，MN=PQ，则只需要知道下列哪条线段的长就可以求出图中阴影部分的周长和( )
A. BFB. EHC. CGD. BC
二、填空题：本题共10小题，每小题3分，共30分。
9.如果把向东走22m记作+22m，那么向西走15m记作 m．
10.比较大小：−23 −35.(填“”或“=”)
11.华为Mate60RS非凡大师配备了令人惊艳的6.82英寸OLED显示屏，能够呈现出10.7亿种色彩，无论是视觉效果还是操作流畅度都达到了业界领先水平，则10.7亿用科学记数法表示为 ．
12.如果单项式3x2ym−3与xn+1y3的是同类项，那么m+n= ．
13.点A在数轴上距原点1个单位长度，且位于原点左侧，若将A点向右移动5个单位长度，这时A点表示的数是 ．
14.若a、b互为相反数，c、d互为倒数，x=2，则a+b2+3cd+x= ．
15.按如图所示的运算程序，两次分别输入5和13，则两次输出的结果的积为 ．
16.若整式3x2+mx−2y+4−3nx2−2x+6y−3的值与字母x的取值无关，则mn的值为 ．
17.当x=2时，代数式ax3+bx+7的值为4，则当x=−2时，代数式ax3+bx+7的值为 ．
18.规定：符号[x]叫做取整符号，它表示不超过x的最大整数．
例如：5=5，2.6=2，0.2=0．
现在有一列非负数a1,a2,a3,…，已知a1=10，当n≥2时，an=a n−1+1−5n−15−n−25，则a2024的值为 ．
三、计算题：本大题共2小题，共12分。
19.计算：
(1)−8+4÷−2；
(2)−20++3−−5−+7
(3)−56×47−38+114
(4)−14−1−0.5×13×2−−32
20.化简：
(1)9a−4a+3b−5a−2b；
(2)5a2−3ab+7−75ab−4a2+7．
四、解答题：本题共6小题，共48分。解答应写出文字说明，证明过程或演算步骤。
21.(本小题8分)
先化简，再求值：−3a2b+ab2−2a2b−1−2ab2−2，其中a=−1,b=2．
22.(本小题8分)
某飞行表演队在航展上表演特技飞行，表演从空中某一位置开始，上升的高度记作正数，下降的高度记作负数，五次特技飞行高度记录如下(单位：km)：+2.5，−1.2，+1.1，−1.5，+0.8．
(1)求飞机最后所在的位置比开始位置高还是低？高了或低了多少千米？
(2)若飞机每上升1km需消耗6L燃油，每下降1km需消耗4L燃油，则飞机在这5次特技飞行中，一共消耗多少升燃油？
23.(本小题8分)
已知三个实数a、b、c在数轴上对应的点如图所示．
(1)判断正负：a−b 0，c−a 0，c+b 0，a+b 0.
(2)根据(1)中的判断化简：a−b+c−a−c+b−a+b．
24.(本小题8分)
【阅读理解】我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，解决问题的策略一般都是进行一定的转化，其中“作差法”就是常用的方法之一．作差法：就是通过作差、变形，利用差的符号确定它们的大小，即要比较代数式A、B的大小，只要算A−B的值，若A−B>0，则A>B；若A−B=0，则A=B；若A−B0)得到如图(2)所示的长方形，此长方形的面积为S1；将正方形的边长增加a，得到如图(3)所示的大正方形，此时正方形的面积为S2=16+8a+a2.请先判断S1与S2的大小关系，并说明理由．
25.(本小题8分)
某超市“双十一”期间进行商品促销活动，一次性买够一定重量的牛肉就会有优惠，原价为50元/千克的牛肉按照如下活动进行售卖：
(1)某餐馆打算一次性购买牛肉45千克，若在促销期间购买，则该餐馆会比按原价购买节省多少钱？
(2)若某顾客打算一次性购买牛肉a千克，请用含a的代数式表示促销期间这个顾客的花费；
(3)促销期间，某校食堂准备购买80千克牛肉，采购员计划了两种购买方案：
方案一：一次性购买牛肉80千克；
方案二：分两次购买，每次购买牛肉40千克；
试判断哪种方案更加划算？并计算出按照两种方案购买相差的金额．
26.(本小题8分)
如图1.在数轴上点M表示的数为m，点N表示的数为n，点M到点N的距离记为MN.我们规定：MN的大小用位于右边的点表示的数减去左边的点表示的数表示，即MN=n−m.请用上面的知识解答下面的问题：如图2：在数轴上点A表示数a，点B表示数b，点C表示数c，b是最大的负整数．且a，c满足a+32与c−5互为相反数．
(1)a= ，b= ，c= ；
(2)若将数轴折叠，使得A点与C点重合，则点B与表示数 的点重合；
(3)点A、B、C开始在数轴上运动，若点A以每秒2个单位长度的速度向左运动，同时，点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动，假设t秒钟后．
①请问：6BC−4AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值；
②探究：若点A，C向右运动，点B向左运动，速度保持不变，3BC−4AB的值是否随着时间的变化而改变？若变化，请说明理由；若不变，请求其值．
参考答案
1.A
2.B
3.D
4.A
5.B
6.D
7.C
8.B
9.−15
10.<
×109
12.7
13.4
14.1或5/5或1
15.15
16.−2
17.10
18.13
19.【小题1】
解：−8+4÷−2
=−8+−2
=−10；
【小题2】
解：−20++3−−5−+7
=−20+3+5−7
=−19；
【小题3】
解：−56×47−38+114
=−56×47−−56×38+−56×114
=−32+21−4
=−15；
【小题4】
解：−14−1−0.5×13×2−−32
=−1−12×13×2−9
=−1−16×−7
=−1+76
=16．

20.【小题1】
解：9a−4a+3b−5a−2b
=9−4−5a+3−2b
=b；
【小题2】
解：5a2−3ab+7−75ab−4a2+7
=5a2−3ab+7−35ab+28a2−49
=5+28a2+−3−35ab+7−49
=33a2−38ab−42．

21.解：−3a2b+ab2−2a2b−1−2ab2−2
=−3a2b−3ab2−2a2b+2−2ab2−2
=−5a2b−5ab2，
当a=−1,b=2时，原式=−5×−12×2−5×−1×22=−10+20=10．

22.【小题1】
+2.5+−1.2++1.1+−1.5++0.8=1.7km．
答：飞机最后所在的位置比开始位置高，高了1.7km．
【小题2】
2.5+1.1+0.8×6+1.2+1.5×4
=26.4+10.8
=37.2L．
答：一共消耗37.2L燃油．

23.【小题1】
<
>
>

【小题2】
3x+5y>2x+6y
理由如下：3x+5y−2x+6y
=3x+5y−2x−6y
=x−y，
∵x>y
∴x−y>0，
∴3x+5y>2x+6y，
【小题3】
S1