2024-2025学年江苏省南京市致远初级中学期中质量监测八年级（上）数学试卷（含答案）

这是一份2024-2025学年江苏省南京市致远初级中学期中质量监测八年级（上）数学试卷（含答案），共12页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
1.下列各数是无理数的是( )
A. 4B. 2C. 38D. 3.1415926
2.如图，△ABC≌△ADC，∠B=80∘，∠BCA=65∘，则∠DAC的度数是( )
A. 35°B. 40°C. 50°D. 60°
3.如图，在△ABC中，∠C=90°，AC=3，BC=2.以AB为一条边向三角形外部作正方形，则正方形的面积是( )
A. 5B. 6C. 12D. 13
4.如图，一棵大树在一次强台风中于离地面10m处折断倒下，倒下部分的树梢到树的距离为24m，则这棵大树折断处到树顶的长度是( )
A. 10mB. 15mC. 26mD. 30m
5.如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF=6，CF=2，则AC的长度为( )
A. 6B. 7C. 8D. 9
6.如图，已知∠ABC=∠DCB，添加以下条件，不能判定▵ABC≌▵DCB的是( )
A. AB=DCB. BE=CEC. AC=DBD. ∠A=∠D
7.如图，在▵ABC中，∠ACB=90∘,∠B=30∘,AD平分∠BAC，E是AD中点，若BD=9，则CE的长为( )
A. 3B. 3.5C. 4D. 4.5
8.如图，等边三角形ABC的边长为8，A、B、A1三点在一条直线上，且▵ABC≌▵A1BC1.若D为线段BC1上一动点，则AD+CD的最小值是( )
A. 10B. 12C. 16D. 18
二、填空题：本题共10小题，每小题3分，共30分。
9.实数4的算术平方根为 ．
10.若一直角三角形两直角边长分别为6和8，则斜边长为 ．
11.已知一个直角三角形斜边上的中线长为8cm，则它的斜边长为 cm．
12.等边三角形的边长为2，则这个三角形的高的长是 ．
13.点P在第二象限，且到x轴，y轴的距离分别为2、3，则点P的坐标是 ．
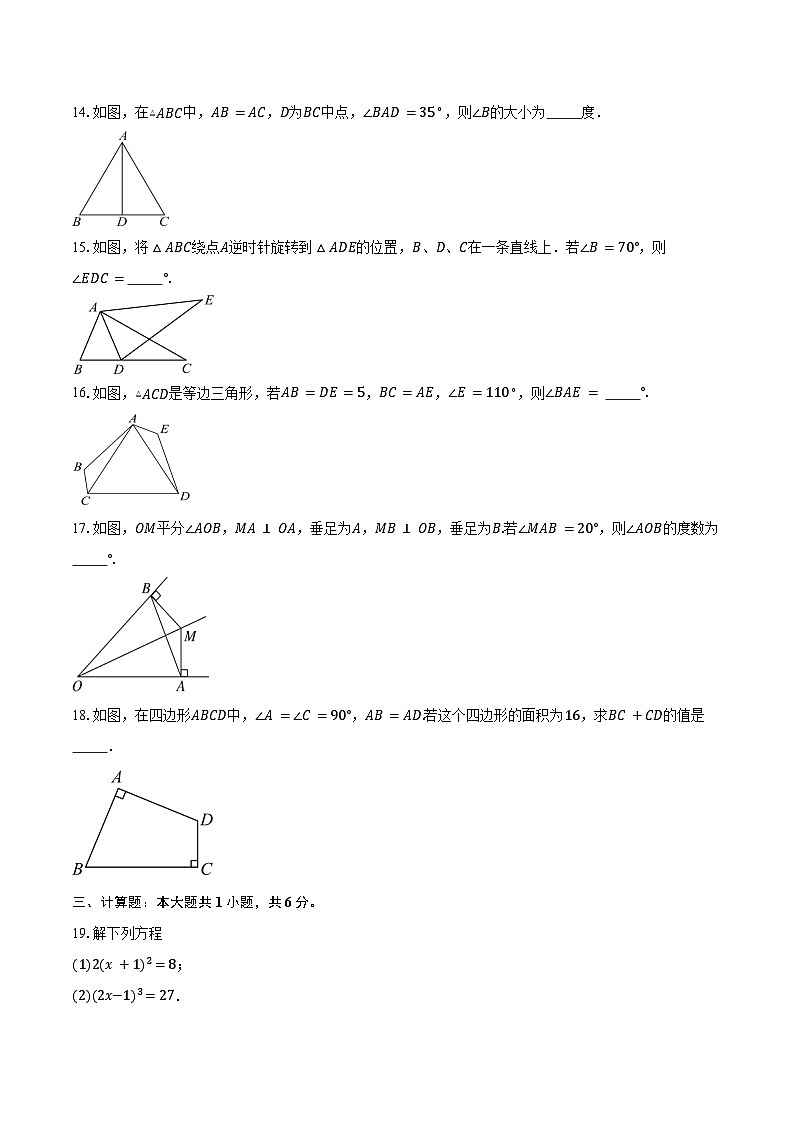
14.如图，在▵ABC中，AB=AC，D为BC中点，∠BAD=35∘，则∠B的大小为 度．
15.如图，将△ABC绕点A逆时针旋转到△ADE的位置，B、D、C在一条直线上．若∠B=70°，则∠EDC= °.
16.如图，▵ACD是等边三角形，若AB=DE=5，BC=AE，∠E=110∘，则∠BAE= °.
17.如图，OM平分∠AOB，MA⊥OA，垂足为A，MB⊥OB，垂足为B.若∠MAB=20°，则∠AOB的度数为 °.
18.如图，在四边形ABCD中，∠A=∠C=90°，AB=AD.若这个四边形的面积为16，求BC+CD的值是 ．
三、计算题：本大题共1小题，共6分。
19.解下列方程
(1)2x+12=8；
(2)2x−13=27．
四、解答题：本题共8小题，共64分。解答应写出文字说明，证明过程或演算步骤。
20.(本小题8分)
如图，AB=CD，∠B=∠C，点F、E在BC上，BF=CE.求证：AE=DF．
21.(本小题8分)
已知：如图，AD//BC，AD=BC.求证：AB//CD．
22.(本小题8分)
如图，在8×8的正方形网格中，每个小正方形的边长都是1，已知▵ABC的三个顶点在格点上．
(1)画出▵ABC关于直线l对称的▵A1B1C1；
(2)在直线l上找一点P，使PA+PB的长最短；(不写画法，保留画图痕迹)；
(3)求▵ABC的面积．
23.(本小题8分)
如图，▵ABC中，AB=AC，∠A=50∘，DE是腰AB的垂直平分线，求∠DBC的度数．
24.(本小题8分)
如图，已知某开发区有一块四边形空地ABCD.现计划在该空地上种植草皮，经测量∠ADC=90°，CD=3m，AD=4m，BC=12m，AB=13m.若每平方米草皮需200元，则在该空地上种植草皮共需多少元?
25.(本小题8分)
如图，△ABC中，D是BC延长线上一点，满足CD=AB，过点C作CE // AB且CE=BC，连接DE并延长，分别交AC、AB于点F、G．
(1)求证：△ABC≌△DCE；
(2)若∠B=50°，∠D=22°，求∠AFG的度数．
26.(本小题8分)
如图，已知直线a/​/b，点A为直线a、b之间的一定点，点B、C分别在直线a、b上，按照下列要求作出等边▵ABC.要求：①用直尺和圆规作图；②保留作图的痕迹；③写出必要的文字说明．
(1)如图，已知点A到直线a、b的距离相等；
(2)如图，已知点A为直线a、b间任意一点．
27.(本小题8分)
【问题情境】
教材中小明用4张全等的直角三角形纸片拼成图1，利用此图，可以验证勾股定理吗？
【探索新知】
从面积的角度思考，不难发现：
大正方形的面积=小正方形的面积+4个直角三角形的面积．
从而得数学等式：(a+b)2=c2+4×12ab，化简证得勾股定理：a2+b2=c2．
【初步运用】
(1)如图1，若b=2a，则小正方形面积:大正方形面积= ；
(2)现将图1中上方的两直角三角形向内折叠，如图2，若a=4，b=6，此时小正方形内空白部分的面积为 ；
(3)如图3，将这四个直角三角形紧密地拼接，形成风车状，已知外围轮廓(实线)的周长为24，OC=3，该风车状图案的面积为 ；
(4)如图4，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3=30，则S2= ．
(5)如果用三张含60∘的全等三角形纸片，能否拼成一个特殊图形呢？带着这个疑问，小丽拼出图5的等边三角形，你能否仿照勾股定理的验证，发现含60∘的三角形三边a、b、c之间的关系，写出此等量关系式及其推导过程．
参考答案
1.B
2.A
3.D
4.C
5.C
6.C
7.D
8.C
9.2
10.10
11.16
12. 3
13.−3,2
14.55
15.40
16.130
17.40
18.8
19.【小题1】
解：2x+12=8，
x+12=4，
∴x+1=±2，
∴x1=−3，x2=1；
【小题2】
解：2x−13=27，
∴2x−1=3，
∴x=2．

20.证明：∵BF=CE，
∴BE=CF，
在▵ABE和▵DCF中，
AB=CD∠B=∠CBE=CF,
∴▵ABE≌▵DCF(SAS)，
∴AE=DF．

21.证明：∵AD//BC，
∴∠CAD=∠ACB，
∵AD=BC，AC=CA，
∴▵ABC≌▵CDASAS，
∴∠BAC=∠ACD，
∴AB/​/CD．

22.【小题1】
解：如图，▵A1B1C1即为所求；
【小题2】
解：如图，点P即为所求；
【小题3】
解：▵ABC的面积为：2×4−12×1×2−12×1×3−12×1×4=72

23.解：∵AB=AC，
∴∠ABC=∠C，
又∵∠A=50∘，
∴∠ABC=12(180∘−50∘)=65∘，
∵ DE是腰AB的垂直平分线，
∴AD=BD，
∴∠ABD=∠A=50∘，
∴∠DBC=∠ABC−∠ABD=15∘．

24.解：连接AC
在Rt△ACD中，
∵CD=3，AD=4
∴AC= AD2+CD2=5
又∵BC=12，AB=13
∴AC2+BC2=AB2
∴∠ACB=90°
∴S四边形ABCD=SΔACB−SΔACD=12×5×12−12×3×4=24m2
∴共需24×200=4800元

25.【小题1】
证明：∵CE // AB，
∴∠B=∠DCE，
在△ABC与△DCE中，
BC=CE∠ABC=∠DCEBA=CD,
∴△ABC≌△DCE(SAS)；
【小题2】
解：∵△ABC≌△DCE，∠B=50°，∠D=22°，
∴∠ECD=∠B=50°，∠A=∠D=22°，
∵CE // AB，
∴∠ACE=∠A=22°，
∵∠CED=180°−∠D−∠ECD=180°−22°−50°=108°，
∴∠AFG=∠DFC=∠CED−∠ACE=108°−22°=86°．

26.【小题1】
解：如图，▵ABC是等边三角形；
【小题2】
解：如图，▵ABC是等边三角形．

27.【小题1】
5:9
【小题2】
28
【小题3】
24
【小题4】
10
【小题5】
解：a2+b2−ab=c2．
设大正三角形的高为ℎ大，中心小正三角形的高为ℎ小，三个全等三角形的高为ℎ单．
由图可知大正三角形面积=三个全等三角形面积+小正三角形面积，
ℎ大= a+b2−a+b22= 34a+b2= 32a+b，
∴大等边三角形的面积S大=12×a+b× 32a+b= 34a+b2，
ℎ小= c2−c22= 34c2= 32c，
∴小等边三角形的面积S小=12×c× 32c= 34c2，
ℎ单= b2−b22= 32b，
S单=12×a× 32b= 34ab，
∴三个这样的三角形面积之和为3× 34ab，
∴ 34a+b2= 34c2+3× 34ab，
a+b2=c2+3ab，
∴a2+b2−ab=c2．