浙教版八年级数学上学期期末【全真模拟卷02】（2份，原卷版+解析版）

这是一份浙教版八年级数学上学期期末【全真模拟卷02】（2份，原卷版+解析版），文件包含浙教版八年级数学上学期期末全真模拟卷02原卷版doc、浙教版八年级数学上学期期末全真模拟卷02解析版doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
考生注意：
本试卷26道试题，满分120分，考试时间100分钟．
本试卷分设试卷和答题纸．试卷包括试题与答题要求．作答必须涂（选择题）或写（非选择题）在答题纸上，在试卷上作答一律不得分．
答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息．
一．选择题（共10小题每题3分，满分30分）
1．点A（﹣5，3）所在的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【分析】根据各象限内点的坐标符号可得其所在象限．
【解答】解：∵点P的坐标为（﹣5，3），
∴点P的横坐标为负数，纵坐标为正数，
∴点P在第二象限，
故选：B．
【点评】本题主要考查点的坐标，解题的关键是掌握四个象限内点的坐标符号特点．
2．如图，已知图形X和直线l．以直线l为对称轴，图形X的轴对称图形是（ ）
A．B．
C．D．
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【解答】解：沿直线l折叠，只有选项D能使直线两旁的部分能够互相重合，
故选：D．
【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
3．x＝1是不等式x﹣b＜0的一个解，则b的值不可能是（ ）
A．1B．2C．3D．4
【分析】解不等式x﹣b＜0可得x＜b，再根据x＝1是不等式x﹣b＜0的一个解即可．
【解答】解：解不等式x﹣b＜0，得x＜b，
因为x＝1是不等式x﹣b＜0的一个解，
所以b的值不可能是1．
故选：A．
【点评】本题主要考查解一元一次不等式，解题的关键是根据不等式的解的概念得出关于m的不等式并熟练掌握解一元一次不等式的能力．
4．不等式的解在数轴上如图所示，则这个不等式的解是（ ）
A．x＞﹣1B．x≥﹣1C．x＜﹣1D．x≤﹣1
【分析】根据不等式的解集在数轴上的表示方法即可得出结论．
【解答】解：∵﹣1处是空心圆点，且折线向右，
∴x＞﹣1．
故选：A．
【点评】本题考查的是在数轴上表示不等式的解集，熟知“小于向左，大于向右”是解答此题的关键．
5．如图给出的三角形有一部分被遮挡，则这个三角形可能是（ ）
A．直角三角形B．锐角三角形C．钝角三角形D．等边三角形
【分析】根据三角形的分类：直角三角形、锐角三角形、钝角三角形进行判断即可．
【解答】解：观察图形知，这个三角形可能是锐角三角形；
故选：B．
【点评】此题主要考查了三角形，关键是掌握三角形的分类．
6．下列叙述有误的是（ ）
A．三角形任何两边的和大于第三边
B．对称轴一定垂直平分连结两个对称点的线段
C．所有的等边三角形都是全等图形
D．物体在平面上的位置可以用第几行第几列来确定，也可以用方向和距离来确定
【分析】根据三角形三边关系可判定A，由轴对称的性质可判定B，由全等三角形定义可判定C，根据位置确定的方法可判定D．
【解答】解：三角形任何两边的和大于第三边，故A说法正确，不符合题意；
对称轴垂直平分连结两个对称点的线段，故B说法正确，不符合题意；
等边三角形有大有小，不一定全等，故C说法错误，符合题意；
物体在平面上的位置除了用有序实数对，还可以用方向和距离来确定，故D说法正确，不符合题意；
故选：C．
【点评】本题考查三角形三边关系，轴对称的性质，全等三角形判定及位置的确定，解题的关键是掌握相关的定义、定理．
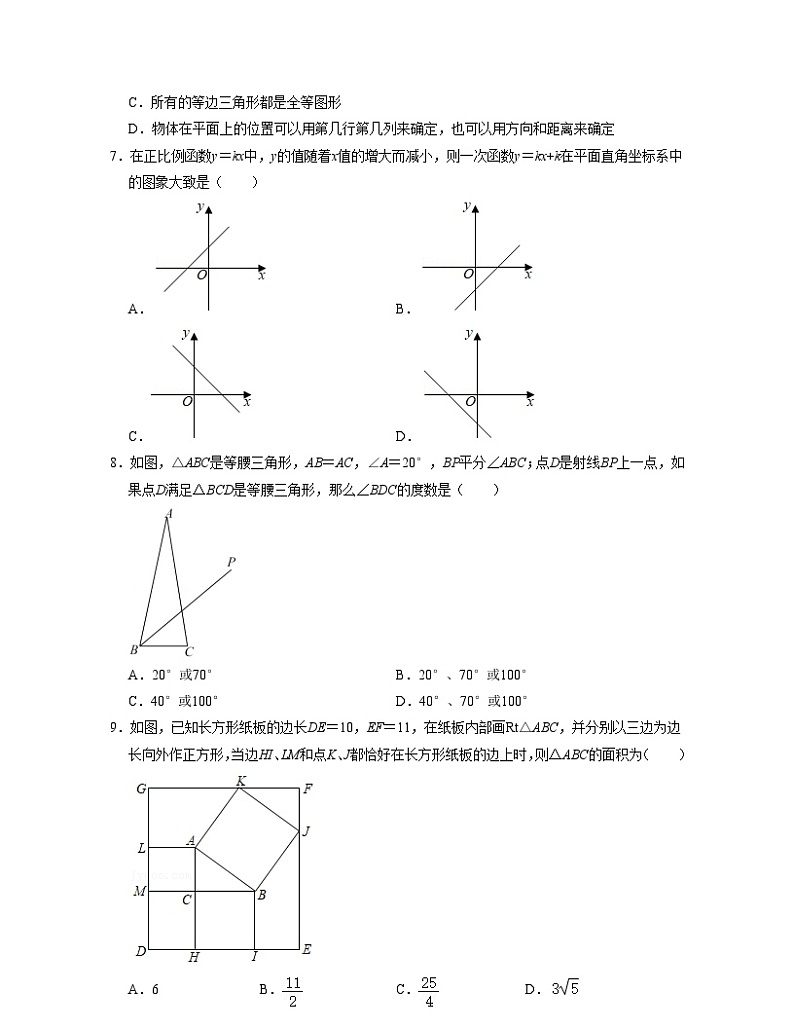
7．在正比例函数y＝kx中，y的值随着x值的增大而减小，则一次函数y＝kx+k在平面直角坐标系中的图象大致是（ ）
A．B．
C．D．
【分析】由于正比例函数y＝kx（k≠0）函数值随x的增大而减小，可得k＜0，然后，判断一次函数y＝kx+k的图象经过象限即可．
【解答】解：∵正比例函数y＝kx（k≠0）函数值随x的增大而减小，
k＜0，
∴一次函数y＝kx+k的图象经过二、三、四象限；
故选：D．
【点评】本题主要考查了一次函数的图象，掌握一次函数y＝kx+b，当k＞0，b＞0时，图象过一、二、三象限；当k＞0，b＜0时，图象过一、三、四象限；k＜0，b＞0时，图象过一、二、四象限；k＜0，b＜0时，图象过二、三、四象限．
8．如图，△ABC是等腰三角形，AB＝AC，∠A＝20°，BP平分∠ABC；点D是射线BP上一点，如果点D满足△BCD是等腰三角形，那么∠BDC的度数是（ ）
A．20°或70°B．20°、70°或100°
C．40°或100°D．40°、70°或100°
【分析】由于△BCD中，腰底不确定，故需要分情况讨论，然后根据等腰三角形的性质即可求出答案．
【解答】解：当BC＝CD时，如图所示，
∵∠A＝20°，AB＝AC，
∴∠ABC＝80°，
∵BP平分∠ABC，
∴∠CBD＝40°，
∵BC＝CD，
∴∠CBD＝∠BDC＝40°，
当BD＝BC时，如图所示，
∵∠A＝20°，AB＝AC，
∴∠ABC＝80°，
∵BP平分∠ABC，
∴∠CBD＝40°，
∵BD＝BC，
∴∠BDC＝70°．
当DB＝DC时，如图所示，
∵∠A＝20°，AB＝AC，
∴∠ABC＝80°，
∵BP平分∠ABC，
∴∠CBD＝40°，
∵BD＝CD，
∴∠BDC＝100°，
故选：D．
【点评】本题考查等腰三角形的判定和性质，解题的关键是熟练运用等腰三角形的性质，本题属于中等题型．
9．如图，已知长方形纸板的边长DE＝10，EF＝11，在纸板内部画Rt△ABC，并分别以三边为边长向外作正方形，当边HI、LM和点K、J都恰好在长方形纸板的边上时，则△ABC的面积为（ ）
A．6B．C．D．
【分析】由“AAS”可证△ABC≌△BJQ，可得AC＝BQ，同理可证AR＝BC，由线段的和差关系可得AC+2BC＝11，2AC+BC＝10，可求AC，BC的长，即可求解．
【解答】解：如图，延长CA交GF于R，延长CB交EF于Q，
∵四边形ACML，ABJK是正方形，
∴AC＝CM，CM⊥GD，AB＝BJ，∠ABJ＝90°，
∵四边形GFED是矩形，
∴GD∥EF，
∴MC⊥EF，
∴∠BQJ＝∠ACB＝90°＝∠ABJ，
∴∠ABC+∠BAC＝90°＝∠ABC+∠QBJ，
∴∠BAC＝∠QBJ，
在△ABC和△BJQ中，
，
∴△ABC≌△BJQ（AAS），
∴AC＝BQ，
同理可证：AR＝BC，
∵AC+CH+AR＝11，MC+BC+BQ＝10，
∴AC+2BC＝11，2AC+BC＝10，
∴AC＝3，BC＝4，
∴S△ABC＝×AC×BC＝×3×4＝6，
故选：A．
【点评】本题考查了矩形的性质，正方形的性质，全等三角形的判定和性质，证明三角形全等是解题的关键．
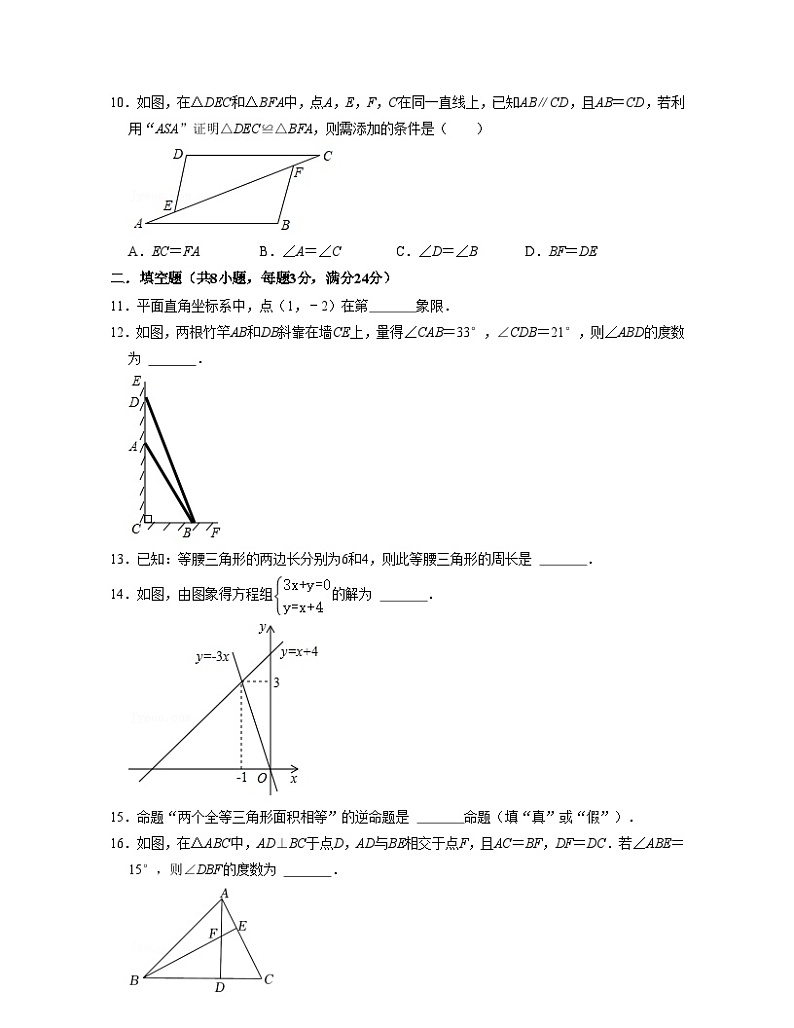
10．如图，在△DEC和△BFA中，点A，E，F，C在同一直线上，已知AB∥CD，且AB＝CD，若利用“ASA”证明△DEC≌△BFA，则需添加的条件是（ ）
A．EC＝FAB．∠A＝∠CC．∠D＝∠BD．BF＝DE
【分析】根据平行线的性质得出∠A＝∠C，再根据全等三角形的判定定理ASA推出即可．
【解答】解：需添加的条件是∠D＝∠B，
理由是：∵AB∥CD，
∴∠A＝∠C，
在△DEC和△BFA中，
，
∴△DEC≌△BFA（ASA），
故选：C．
【点评】本题考查了平行线的性质和全等三角形的判定，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，两直角三角形全等还有HL．
二．填空题（共8小题，每题3分，满分24分）
11．平面直角坐标系中，点（1，﹣2）在第 四 象限．
【分析】依据各象限坐标的符号判断即可．
【解答】解：∵该点的横坐标＞0，纵坐标＜0，
∴该点位于第四象限．
故答案为：四．
【点评】本题主要考查的是点的坐标，掌握各象限点的坐标符号是解题的关键．
12．如图，两根竹竿AB和DB斜靠在墙CE上，量得∠CAB＝33°，∠CDB＝21°，则∠ABD的度数为 12° ．
【分析】根据三角形的外角的性质列式计算，得到答案．
【解答】解：∵∠CAB是△ABD的外角，∠CAB＝33°，∠CDB＝21°，
∴∠ABD＝∠CAB﹣∠CDB＝12°，
故答案为：12°．
【点评】本题考查的是三角形的外角的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．
13．已知：等腰三角形的两边长分别为6和4，则此等腰三角形的周长是 16或14 ．
【分析】分6是腰长和底边两种情况，利用三角形的三边关系判断，然后根据三角形的周长的定义列式计算即可得解．
【解答】解：①6是腰长时，三角形的三边分别为6、6、4，能组成三角形，
周长＝6+6+4＝16，
②6是底边时，三角形的三边分别为6、4、4，能组成三角形，
周长＝6+4+4＝14，
综上所述，三角形的周长为16或14．
故答案为：16或14．
【点评】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
14．如图，由图象得方程组的解为 ．
【分析】两直线的交点坐标就是所求．
【解答】解：由图象知两直线交于点（﹣1，3），
∴二元一次方程组的解是，
故答案为：．
【点评】本题考查了一次函数与二元一次方程组的关系，我们可以用方程组的解来确定函数图象的交点坐标；反之，也可用画函数图象来解方程组．
15．命题“两个全等三角形面积相等”的逆命题是 假 命题（填“真”或“假”）．
【分析】写出这个命题的逆命题，根据全等三角形的判定判断即可．
【解答】解：命题“两个全等三角形面积相等”的逆命题是如果两个三角形的面积相等，那么这两个三角形全等，是假命题；
故答案为：假．
【点评】本题考查的是命题的真假判断、逆命题的概念，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．
16．如图，在△ABC中，AD⊥BC于点D，AD与BE相交于点F，且AC＝BF，DF＝DC．若∠ABE＝15°，则∠DBF的度数为 30° ．
【分析】首先根据“HL”证明Rt△BDF≌Rt△ADC，再利用全等三角形的性质即可解决问题．
【解答】解：∵AD⊥BC，
∴∠BDF＝∠ADC＝90°，
在Rt△BDF和Rt△ADC中，
，
∴Rt△BDF≌Rt△ADC （HL），
∴AD＝BD，
∴∠ABD＝∠DAB＝45°，
∵∠ABE＝15°，
∴∠DBF＝∠ABD﹣∠ABE＝45°﹣15°＝30°．
故答案为：30°．
【点评】本题考查全等三角形的判定和性质，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
17．关于x的不等式组只有一个解，则a与b的关系是 2a＝3b ．
【分析】分别求出每一个不等式的解集，根据不等式组的解的情况得出关于a、b的等式，化简可得答案．
【解答】解：由3x﹣a≥0，得：x≥，
由2x﹣b≤0，得：x≤，
∵不等式组只有1个解，
∴＝，
∴2a＝3b，
故答案为：2a＝3b．
【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
18．如图，在△ABC中，∠ACB＝90°，AC＝8，BC＝6，D是线段AB的中点，P为直线BC上的一动点，连结DP．过点D作ED⊥DP，交直线AC于点E，连结EP．若CP＝3，则AE的长为 4或 ．
【分析】分点P在BC上或P在BC延长线上两种情形，当点P在BC上时，可知DP是△ABC的中位线，可得四边形DPCE是矩形，可得答案；当点P在BC延长线上时，作BH∥AC，交ED延长线于H，可知△AED≌△BHD（AAS），得AE＝BH，DE＝DH，设AE＝BH＝x，由勾股定理得，（8+x）2+32＝92+x2，解方程即可得出答案．
【解答】解：当点P在BC上时，
∵CP＝3，BC＝6，
∴点P是BC的中点，
∵D是线段AB的中点，
∴DP∥AC，
∴∠EDP＝∠DPC＝90°，
∵∠ACB＝90°，
∴四边形DPCE是矩形，
∴DE∥BC，
∴AE＝AC＝4；
当点P在BC延长线上时，作BH∥AC，交ED延长线于H，
则△AED≌△BHD（AAS），
∴AE＝BH，DE＝DH，
∵DE⊥DP，
∴DP垂直平分EH，
∴PE＝PH，
设AE＝BH＝x，由勾股定理得，
（8+x）2+32＝92+x2，
∴x＝，
∴AE＝，
故答案为：4或．
【点评】本题主要考查了全等三角形的判定与性质，三角形中位线定理，矩形的判定与性质，勾股定理等知识，作辅助线构造全等三角形是解题的关键．
三．解答题（共8小题，满分66分）
19．解不等式组．
【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集．
【解答】解：解不等式①，得：x＞1，
解不等式②，得：x≤2，
则不等式组的解集为1＜x≤2．
【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
20．已知点P（a﹣2，2a+8），分别根据下列条件求出点P的坐标．
（1）点P在x轴上；
（2）点Q的坐标为（1，5），直线PQ∥y轴．
【分析】（1）利用x轴上点的坐标性质纵坐标为0，进而得出a的值，即可得出答案；
（2）利用平行于y轴直线的性质，横坐标相等，进而得出a的值，进而得出答案．
【解答】解：（1）∵点P（a﹣2，2a+8）在x轴上，
∴2a+8＝0，
∴a＝﹣4，
∴点P（﹣6，0）；
（2）∵点Q的坐标为（1，5），直线PQ∥y轴，
∴a﹣2＝1，
解得：a＝3，
故2a+8＝14，
则P（1，14）．
【点评】此题主要考查了坐标与图形性质，用到的知识点为：点到两坐标轴的距离相等，那么点的横纵坐标相等或互为相反数以及点在坐标轴上的点的性质．
21．如图，D是△ABC的边AB上一点，CF∥AB，DF交AC于E点，DE＝EF．
（1）求证：△ADE≌△CFE．
（2）若AB＝5.5，CF＝4，求BD的长．
【分析】（1）利用角角边定理判定即可；
（2）利用全等三角形对应边相等可得AD的长，用AB﹣AD即可得出结论．
【解答】（1）证明：∵CF∥AB，
∴∠ADF＝∠F，∠A＝∠ECF．
在△ADE和△CFE中，
，
∴△ADE≌△CFE（AAS）．
（2）∵△ADE≌△CFE，
∴AD＝CF＝4．
∴BD＝AB﹣AD＝5.5﹣4＝1.5，
答：BD的长为1.5．
【点评】本题主要考查了全等三角形的判定与性质．选择合适的判定方法是解题的关键．
22．如图，△ABC（∠B＞∠A）．
（1）在边AC上用尺规作图作出点D，使∠CDB＝2∠A（保留作图痕迹）；
（2）在（1）的情况下，连接BD，若CB＝CD，∠A＝35°，求∠C的度数．
【分析】（1）作AB的垂直平分线交AC于D，则DA＝DB，所以∠A＝∠DBA，则根据三角形外角性质可得到∠CDB＝2∠A；
（2）先计算出∠CDB＝70°，再根据等腰三角形的性质由CB＝CD得到∠CBD＝∠CDB＝70°，然后根据三角形内角和计算∠C的度数．
【解答】解：（1）如图，点D为所作；
（2）由（1）得∠CDB＝2∠A＝2×35°＝70°，
∵CB＝CD，
∴∠CBD＝∠CDB＝70°，
∴∠C＝180°﹣70°﹣70°＝40°．
【点评】本题考查了作图﹣复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
23．在平面直角坐标系xOy中，已知点A（2，0），动点P（x，y）在第一象限，且x+y＝8，△OPA的面积为S．
（1）求S关于x的函数表达式和x的取值范围．
（2）求当S＝2时点P的坐标．
（3）OP+PA的最小值为 10 ．
【分析】（1）首先把x+y＝8，变形成y＝8﹣x，再利用三角形的面积求法：×底×高＝S，可以得到S关于x的函数表达式；由P在第一象限，可得到x的取值范围；
（2）把S＝2代入函数解析式即可得答案；
（3）作点O关于y＝8﹣x的对称点D，则OP＝DP，OP+PA＝DP+PA，当D、P、A在同一直线上时，DP+PA最小，即AD的长．
【解答】解：（1）∵x+y＝8，
∴y＝8﹣x，
∴S＝×2×（8﹣x）＝8﹣x，
即S关于x的函数表达式为S＝8﹣x；
∵P（x，y）在第一象限，
∴x＞0且y＞0，
∴x＞0且8﹣x＞0，
∴x的取值范围是0＜x＜8；
（2）∵S＝2，
∴2＝8﹣x，
解得x＝6，
∴y＝8﹣6＝2，
∴当S＝2时，点P的坐标是（6，2）；
（3）作点O关于y＝8﹣x的对称点D，
∴OP＝DP，OP+PA＝DP+PA，
当D、P、A在同一直线上时，DP+PA最小，即AD的长．
设y＝8﹣x与x轴交于点M，与y轴交于点N，连接DM，
∴M（8，0），N（0，8），
∴OM＝ON＝8，
∴∠OMN＝45°，
∵点O、点D关于y＝8﹣x对称，
∴MN垂直平分OD，
∴OM＝DM＝8，∠DMP＝∠OMN＝45°，
∴∠OMD＝90°，
在Rt△AMD中，AM＝OM﹣OA＝6，DM＝8，
∴AD＝10，
∴OP+PA的最小值为10．
故答案为：10．
【点评】此题是一次函数综合题，考查了一次函数的性质，轴对称求最小值，以及三角形的面积，等腰直角三角形的性质，解题时一定要注意自变量的取值范围．
24．某班计划购买A、B两款文具盒作为期末奖品．若购买3盒A款的文具盒和1盒B款的文具盒需用22元；若购买2盒A款的文具盒和3盒B款的文具盒需用24元．
（1）每盒A款的文具盒和每盒B款的文具盒各多少元．
（2）某班决定购买以上两款的文具盒共40盒，总费用不超过210元，那么该班最多可以购买多少盒A款的文具盒？
【分析】（1）设每盒A款的文具盒为x元，每盒B款的文具盒为y元，由题意：若购买3盒A款的文具盒和1盒B款的文具盒需用22元；若购买2盒A款的文具盒和3盒B款的文具盒需用24元．列出二元一次方程组，解方程组即可；
（2）设该班购买m盒A款的文具盒，由题意：某班决定购买以上两款的文具盒共40盒，总费用不超过210元，列出一元一次不等式，解不等式即可．
【解答】解：（1）设每盒A款的文具盒为x元，每盒B款的文具盒为y元，
由题意得：，
解得：，
答：每盒A款的文具盒为6元，每盒B款的文具盒为4元；
（2）设该班购买m盒A款的文具盒，
由题意得：6m+4（40﹣m）≤210，
解得：m≤25，
答：该班最多可以购买25盒A款的文具盒．
【点评】本题考查了一元一次不等式的应用以及二元一次方程组的应用，解题的关键时：（1）找准等量关系，正确列出二元一次方程组；（2）找出数量关系，正确列出一元一次不等式．
25．小聪和小慧去某风景区游览，约好在观景点见面．小聪步行先从景区入口处出发，中途休息片刻后继续以原速度前行，此时小慧乘观光车从景区入口处出发，他们沿相同路线先后到达观景点，如图，l1，l2分别表示小聪与小慧离景区入口的路程y（千米）与时间x（分）之间的关系．根据图象解决下列问题：
（1）小聪步行的速度是 0.1 （千米/分），中途休息 3 分钟．
（2）求小慧离景区入口的路程y（千米）关于时间x（分）函数表达式．
（3）小慧比小聪早几分钟到达观景点？请说明理由．
【分析】（1）根据函数图象中的数据，可以计算出小聪步行的速度和中途休息的时间；
（2）根据（1）中的结果和图象中的数据，可以计算出小聪18分钟时走的路程，然后再设小慧离景区入口的路程y（千米）关于时间x（分）函数表达式，然后代入数据计算即可；
（3）根据题意和图象中的数据，可以分别计算出小聪和小慧到达景点的时间，然后作差，即可得到小慧比小聪早几分钟到达观景点．
【解答】解：（1）由图象可得，
小聪步行的速度为：1÷10＝0.1（千米/分），
中途休息：13﹣10＝3（分钟），
故答案为：0.1，3；
（2）小聪第18分钟步行的路程为：1+（18﹣13）×0.1＝1.5（千米），
则第18分钟时，小聪和小慧相遇，此时他们走的路程为1.5千米，
设小慧离景区入口的路程y（千米）关于时间x（分）函数表达式为y＝kx+b，
∵点（13，0），（18，1.5）在该函数图象上，
∴，
解得，
即小慧离景区入口的路程y（千米）关于时间x（分）函数表达式为y＝0.3x﹣3.9；
（3）小慧比小聪早10分钟到达观景点，
理由：当y＝3时，3＝0.3x﹣3.9，得x＝23，
小聪到达景点用的总的时间为：13+（3﹣1）÷0.1＝33（分钟），
33﹣23＝10（分钟），
即小慧比小聪早10分钟到达观景点．
【点评】本题考查一次函数的应用，利用数形结合的思想解答是解答本题的关键．
26．【证明体验】
（1）如图1，在△ABC中，AD为BC边上的中线，延长AD至E，使DE＝AD，连结BE．求证：△ACD≌△EBD．
【迁移应用】
（2）如图2，在△ABC中，AC＝5，BC＝13，D为AB的中点，DC⊥AC．求△ABC面积．
【拓展延伸】
（3）如图3，在△ABC中，∠ABC＝90°，D是BC延长线上一点，BC＝CD，F是AB上一点，连结FD交AC于点E，若AF＝EF＝2，BD＝6，求ED的长．
【分析】（1）根据SAS证明三角形全等；
（2）如图2中，延长CD到T，使得DT＝CD，连接BT．由（1）可知△ADC≌△BDT，推出AC＝BT＝5，∠ACD＝∠T＝90°，利用勾股定理求出CT，即可解决问题；
（3）如图3中，延长AC到R，使得CR＝CA，连接DR．证明DE＝DR＝AB，设DE＝DR＝AB＝x，则BF＝x﹣2，DF＝x+2，在Rt△DBF中，根据BF2+BD2＝DF2，构建方程即可解决问题．
【解答】（1）证明：如图1中，
在△ACD和△EBD中，
，
∴△ACD≌△EBD（SAS）；
（2）解：如图2中，延长CD到T，使得DT＝CD，连接BT．
由（1）可知△ADC≌△BDT，
∴AC＝BT＝5，∠ACD＝∠T＝90°，
∴CT＝＝＝12，
∴CD＝DT＝6，
∴S△ACB＝S△ADC+S△CDB＝•AC•DC+•BT•CD＝×5×6+×5×6＝30；
（3）解：如图3中，延长AC到R，使得CR＝CA，连接DR．
由（1）可知，△ACB≌△RCD，
∴AB＝DR，∠A＝∠R，
∵FE＝FA，
∴∠A＝∠AEF，
∵∠AEF＝∠DER，
∴∠DER＝∠R，
∴DE＝DR＝AB，
设DE＝DR＝AB＝x，则BF＝x﹣2，DF＝x+2，
在Rt△DBF中，BF2+BD2＝DF2，
∴（x﹣2）2+62＝（x+2）2，
∴x＝，
∴DE＝．
【点评】本题属于三角形综合题，考查了全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．