初中数学华东师大版（2024）八年级下册2. 菱形的判定教课内容课件ppt

这是一份初中数学华东师大版（2024）八年级下册2. 菱形的判定教课内容课件ppt，共16页。PPT课件主要包含了学习目标，一新课引入，复习回顾菱形的性质，中心＋轴对称，对角线互相平分＋相等，二探究新知，∴OAOC，∵AC⊥BD，∴ABBC等内容，欢迎下载使用。
1.菱形的定义：有一组邻边相等的平行四边形是菱形2.菱形的判定定理1：四条边都相等的四边形是菱形3.菱形的判定定理2：对角线互相垂直的平行四边形是菱形
对边分别平行且四边相等
对角相等（对角线平分对角）
菱形的定义：菱形的特殊性质：
有一组邻边相等的平行四边形是菱形
菱形的对角线互相垂直。
（一）探究：菱形的定义
几何语言：在□ABCD中，AB=BC ∴四边形ABCD是菱形
先判定是平行四边形，再找到一组邻边相等，从而判定为矩形
（二）例题讲解：菱形的定义
解：∵DE//AC ，DF//AB ∴ 四边形AEDF为平行四边形 又∵AD平分∠BAC ∴∠EDA=∠DAC=∠EAD ∴EA=ED ∴四边形AEDF为菱形（有一组邻边相等的平行四边形是菱形）
例1：如图，AD是△ABC的一条角平分线，DE//AC交AB于点E，DF//AB交AC于点F。 求证：四边形AEDF为菱形
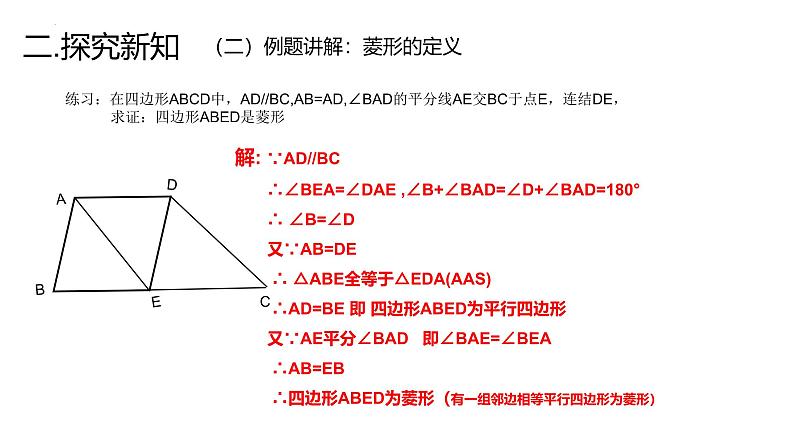
练习：在四边形ABCD中，AD//BC,AB=AD,∠BAD的平分线AE交BC于点E，连结DE， 求证：四边形ABED是菱形
解: ∵AD//BC ∴∠BEA=∠DAE ,∠B+∠BAD=∠D+∠BAD=180° ∴ ∠B=∠D 又∵AB=DE ∴ △ABE全等于△EDA(AAS) ∴AD=BE 即 四边形ABED为平行四边形 又∵AE平分∠BAD 即∠BAE=∠BEA ∴AB=EB ∴四边形ABED为菱形（有一组邻边相等平行四边形为菱形）
练习：在平行四边形ABCD中，点P是对角线AC上一点，PE⊥AB，PF⊥AD，垂足分别为点E、F，且PE=PF， 平行四边形ABCD是菱形吗？为什么？
解: ∵PE⊥AB，PF⊥AD，PE=PF ∴∠PFA=∠PEA=90° , ∴ △PFA全等于△PEA(HL) ∴ ∠PAF=∠PAE 又∵四边形ABCD为平行四边形 ∴∠DCA=∠PAF 即AD=CD ∴四边形ABCD为菱形（有一组邻边相等平行四边形为菱形）
（一）探究：菱形的判定1(四边相等的四边形是菱形)
已知：如图，四边形ABCD的边长，AB=BC=CD=AD
求证：四边形ABCD是菱形
证明： ∵AB=BC=CD=AD 即AB=DC,BC=AD
∴四边形ABCD是菱形（有一组邻边相等的平行四边形是菱形）
∴ 四边形ABCD是平行四边形
（二）例题讲解：菱形的判定1(四边相等的四边形是菱形)
解：∵四边形ABCD为矩形 ∴ ∠A=∠B=∠C=∠D=90° ，AB=DC ,AD=BC 又∵点E、F、G、H分别为四条边的中点 ∴AE=BE=DG=CG ,AH=DH=BF=CF ∴四个三角形全等 即 EH=GH=FG=FE ∴四边形EFGH为菱形（四条边相等的四边形是菱形）
例2：在矩形ABCD中，点E、F、G、H分别为四条边的中点，问四边形EFGH为什么图形，说明理由
练习：AD是∠BAC的平分线，AD的垂直平分线交AB于点E，交AC于点F, 求证：四边形AEDF是菱形
解: ∵AD的垂直平分线交AB于点E，交AC于点F ∴AE=DE ,AF=DF 即∠EAD= ∠EDA, ∠FAD =∠ FDA 又∵AD平分∠BAC ∴ ∠EAD= ∠FAD, ∠EDA =∠ FDA ∴△AED全等于△AFD(ASA) ∴AE=AF=DF=DE ∴四边形ABED为菱形（四条边相等的四边形为菱形）
（一）探究：菱形的判定2(对角线互相垂直的平行四边形是菱形)
已知：如图，平行四边形ABCD中，对角线AC ⊥ BD 求证：平行四边形ABCD是菱形
证明：∵四边形ABCD是平行四边形
∴BD 为AC的线段垂直平分线
∴四边形ABCD为菱形（有一组邻边相等平行四边形为菱形）
例3：在矩形ABCD中，对角线AC的垂直平分线与边AD、BC分别交于点E、F，求证：四边形AFCE为菱形
（二）例题讲解：菱形的判定2(对角线互相垂直的平行四边形是菱形)
解: ∵四边形ABCD为矩形 ∴ ∠1=∠2 ∵EF垂直平分AC，即EF⊥AC ∴ ∠AOE=∠COF=90°,AO=CO ∴△AOE全等于△COF(ASA) 即AE=CF ∴四边形AFCE为平行四边形 ∴四边形AFCE为菱形（对角线互相垂直的平行四边形为菱形）
练习：在矩形ABCD中，直线EF垂直平分线段AC，垂足为点O，与AD、CB延长线交于点E、F， 求证：四边形AFCE为菱形
解: ∵四边形ABCD为矩形 ∴ AD//BC 即AE//CF ∴ ∠AEF=∠CFE 又∵ 直线EF垂直平分线段AC 即EF⊥AC ∴ AO=CO ,∠AOE=∠COF=90° ∴ △AOE全等于△COF（AAS） ∴AE=CF 即四边形AFCE为平行四边形 ∴四边形AFCE为菱形（对角线垂直的平行四边形为菱形）
（二）例题讲解：菱形的特殊性质2(菱形的对角线互相垂直)
练习：在△ABC中，AB=AC,点 D是BC中点，DE⊥AC于点E，DG⊥AB于点G,EK⊥AB于点K， GH⊥AC于点H,EK、GH相交于点F,求证;GE与FD互相垂直平分
解: ∵DE⊥AC于点E，GH⊥AC于点H，DG⊥AB于点G,EK⊥AB于点K， ∴ GH//DE ,GD//KE 即GF//DE ,GD//EF,∠BGD=∠CED=90° ∴ 四边形GDEF为平行四边形 又∵ AB=AC,点 D是BC中点 ∴ BD=CD ,∠B=∠C ∴ △BGD全等于△CED（AAS） ∴GD=ED ∴四边形GDEF为菱形（有一组邻边相等的平行四边形为菱形） ∴GE⊥FD
（二）例题讲解：拓展提升
练习：在菱形ABCD的周长为2p，对角线AC、BD交于点O，AC+BD=q，求菱形ABCD的面积
解: ∵四边形ABCD为菱形, 周长为2p ∴ AD=CD=BC=AB=0.5p ，AC⊥BD,AO=CO ,BO=DO ∵AC+BD=q ∴ AO+DO=0.5q ∴ ∴