初中数学人教版（2024）九年级下册27.3 位似优秀测试题

这是一份初中数学人教版（2024）九年级下册27.3 位似优秀测试题，文件包含人教版数学九年级下册重难点培优训练专题275位似与位似变换综合问题专项提升训练原卷版doc、人教版数学九年级下册重难点培优训练专题275位似与位似变换综合问题专项提升训练解析版doc等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
注意事项：
本试卷满分100分，试题共22题，选择10道、填空6道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
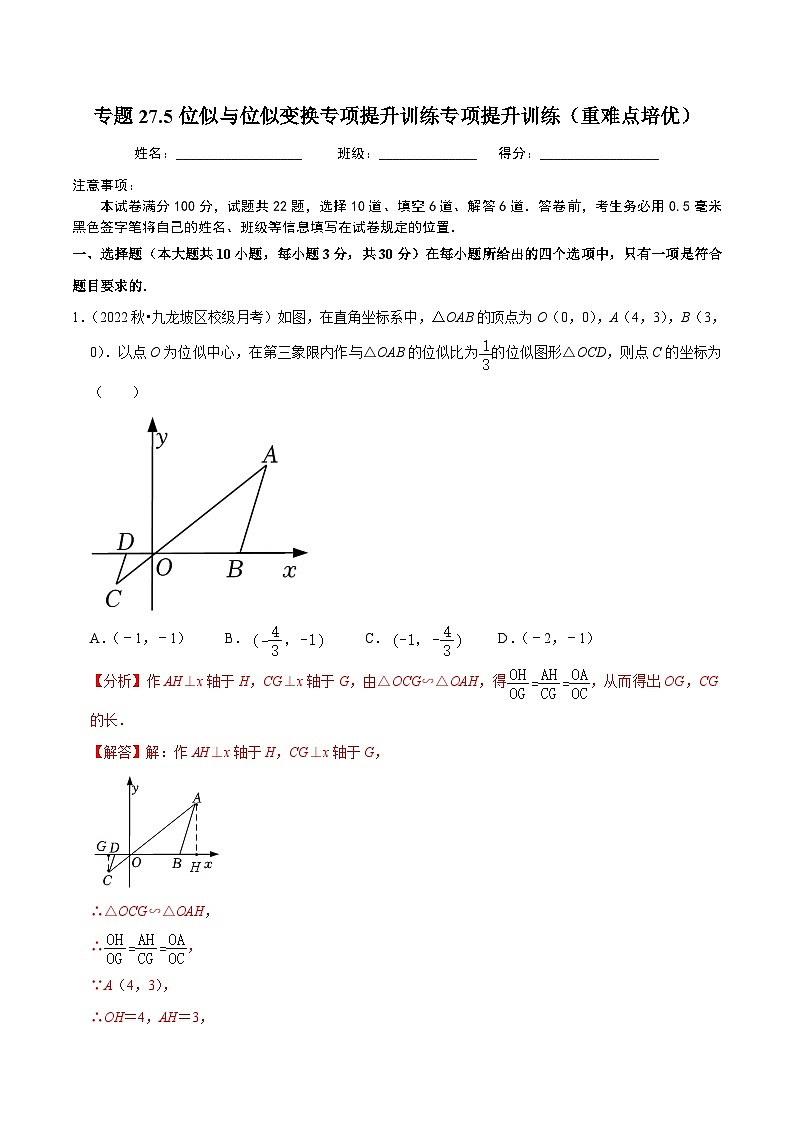
1．（2022秋•九龙坡区校级月考）如图，在直角坐标系中，△OAB的顶点为O（0，0），A（4，3），B（3，0）．以点O为位似中心，在第三象限内作与△OAB的位似比为的位似图形△OCD，则点C的坐标为（ ）
A．（﹣1，﹣1）B．C．D．（﹣2，﹣1）
【分析】作AH⊥x轴于H，CG⊥x轴于G，由△OCG∽△OAH，得，从而得出OG，CG的长．
【解答】解：作AH⊥x轴于H，CG⊥x轴于G，
∴△OCG∽△OAH，
∴，
∵A（4，3），
∴OH＝4，AH＝3，
∵△BOA∽△DOC，且OA：OC＝3，
∴OG＝，CG＝1，
∴C（﹣，﹣1），
故选：B．
2．（2022秋•沙坪坝区校级期中）如图，△ABC与△DEF位似，点O为位似中心，位似比为2：3，若△DEF的周长为6，则△ABC的周长是（ ）
A．16B．9C．6D．4
【分析】根据位似变换的定义、相似三角形的性质计算即可．
【解答】解：∵△DEF和△ABC是位似图形，位似比为2：3，
∴△DEF和△ABC的相似比为2：3，
∴△ABC的周长＝×△DEF的周长＝9，
故选：B．
3．（2022秋•二道区校级期中）如图，以点O为位似中心，把△ABC放大到原来的2倍得到△A'B'C'．以下说法中错误的是（ ）
A．△ABC∽△A'B'C'
B．点A、O、A'三点在同一条直线上
C．AO：AA'＝1：2
D．S△ABC：S△A'B'C′＝1：4
【分析】根据位似的性质对各选项进行判断．
【解答】解：∵点O为位似中心，把△ABC中放大到原来的2倍得到△A'B'C'，
∴△ABC∽△A'B'C'，OA：OA′＝1：2，AB∥A′B′，点A、O、A'三点在同一条直线上，S△ABC：S△A′B′C′＝（）2＝．
故选：C．
4．（2022秋•雁塔区校级月考）在平面直角坐标系中，已知点A（﹣4，2），B（﹣6，﹣4），以原点O为位似中心，相似比为2，把△ABO放大，则点B的对应点B'的坐标是（ ）
A．（﹣3，﹣2）B．（﹣3，﹣2）或（3，2）
C．（﹣12，﹣8）D．（﹣12，﹣8）或（12，8）
【分析】根据位似变换的性质计算，得到答案．
【解答】解：∵以原点O为位似中心，相似比为2，把△ABO放大，B（﹣6，﹣4），
点A的对应点A'的坐标为（﹣6×2，﹣4×2）或（﹣6×（﹣2），﹣4×（﹣2）），即点A'的坐标为（﹣12，﹣8）或（12，8），
故选：D．
5．（2022秋•碑林区校级月考）如图，△ABO三个顶点的坐标分别为A（4，﹣6）、B（6，0）、O（0，0），以原点O为位似中心画一个三角形△A'B'O'，使它与△ABO位似，且位似比是2：1，则点A的对应点A'的坐标是（ ）
A．（2，﹣3）B．（8，﹣12）或（﹣8，12）
C．（2，﹣3）或（﹣2，3）D．（8，﹣12）
【分析】根据位似变换的性质计算即可．
【解答】解：∵以原点O为位似中心，△A'B'O'与△ABO位似，且位似比是2：1，点A的坐标为（4，﹣6），
∴点A的对应点A'的坐标为（4×2，﹣6×2）或（4×（﹣2），﹣6×（﹣2）），即（8，﹣12）或（﹣8，12），
故选：B．
6．（2022春•巴东县期中）如图，在边长为1的正方形网格中，△ABC与△DEF是位似图形，则△ABC与△DEF的相似比为（ ）
A．B．C．D．2
【分析】利用勾股定理求出AB，DE，再利用相似三角形的性质求解，
【解答】解：∵△ABC与△DEF是位似图形，AB，DE是对应边，AB＝2，DE＝，
∴相似比＝＝2，
故选：D．
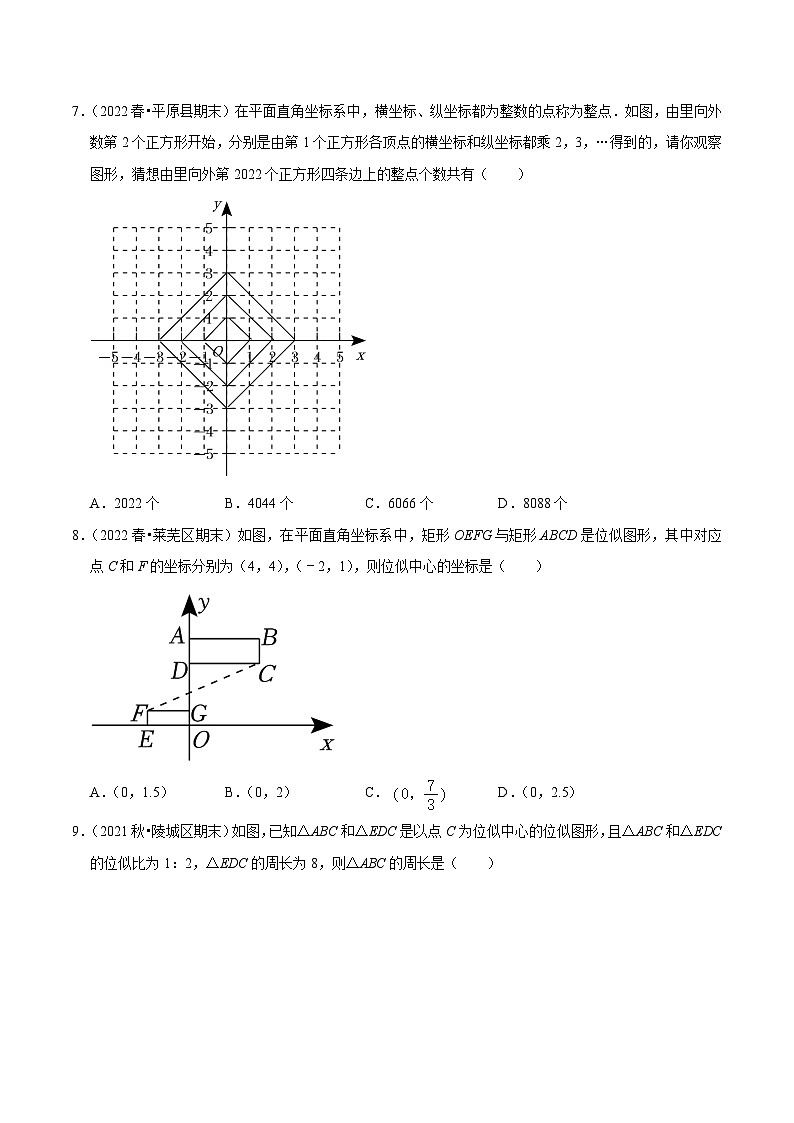
7．（2022春•平原县期末）在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．如图，由里向外数第2个正方形开始，分别是由第1个正方形各顶点的横坐标和纵坐标都乘2，3，…得到的，请你观察图形，猜想由里向外第2022个正方形四条边上的整点个数共有（ ）
A．2022个B．4044个C．6066个D．8088个
【分析】依次找到从内到外的几个正方形上的整数点，得到规律，由规律求得第n个正方形的整点个数．
【解答】解：由内到外规律，第1个正方形边上整点个数为4×1＝4（个），
第2个正方形边上整点个数为4×2＝8（个），
第3个正方形边上整点个数为4×3＝12（个），
第4个正方形边上整点个数为4×4＝16（个），
•••
故第n个正方形边上的整点个数为4n个．
由此可得，由里向外第2022个正方形四条边上的整点个数为：4×2022＝8088．
故选：D．
8．（2022春•莱芜区期末）如图，在平面直角坐标系中，矩形OEFG与矩形ABCD是位似图形，其中对应点C和F的坐标分别为（4，4），（﹣2，1），则位似中心的坐标是（ ）
A．（0，1.5）B．（0，2）C．D．（0，2.5）
【分析】根据位似图形的概念得到FG∥BC，得到△PGF∽△PCD，根据相似三角形的性质求出PC，得到答案．
【解答】解：根据题意得P为位似中心，
由题意得，CD＝4，GF＝2，DG＝3，OG＝1，
∵矩形OEFG与矩形ABCD是位似图形，
∴CD∥GF，
∴△CDP∽△FGP，
∴＝，即 ＝，
解得，GP＝1，
∴OP＝2，
∴位似中心P的坐标为（0，2）．
故选：B．
9．（2021秋•陵城区期末）如图，已知△ABC和△EDC是以点C为位似中心的位似图形，且△ABC和△EDC的位似比为1：2，△EDC的周长为8，则△ABC的周长是（ ）
A．2B．4C．8D．16
【分析】根据位似变换的性质得到△ABC∽△EDC，根据相似三角形的周长比等于相似比计算即可．
【解答】解：∵△ABC和△EDC是以点C为位似中心的位似图形，
∴△ABC∽△EDC，
∵△ABC和△EDC的位似比为1：2，
∴△ABC和△EDC的相似比为1：2，
则△ABC与△EDC的周长比为1：2，
∵△DEC周长为8，
∴△ABC的周长是：4．
故选：B．
10．（2018秋•越秀区校级期末）如图，在平面直角坐标系xOy中，对正方形ABCD及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一个实数a，将得到的点先向右平移m个单位，再向上平移n个单位（m＞0，n＞0），得到正方形A'B'C'D'及其内部的点，其中点A、B的对应点分别为A'，B'．已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F'与点F重合，则点F的坐标是（ ）
A．（1，4）B．（1，5）C．（﹣1，4）D．（4，1）
【分析】首先根据点A到A′，B到B′的点的坐标可得方程组；，解可得a、m、n的值，设F点的坐标为（x，y），点F′点F重合可列出方程组，再解可得F点坐标．
【解答】解：由点A到A′，可得方程组；
由B到B′，可得方程组，
解得，
设F点的坐标为（x，y），点F′点F重合得到方程组，
解得，
即F（1，4）．
故选：A．
二．填空题（共6小题）
11．（2022•钟楼区校级模拟）如图，平面直角坐标系中，点A在x轴正半轴上，且OA＝4，∠BOA＝30°，∠B＝90°，以点O为位似中心，在第一象限内将△AOB放大，使相似比为2：1，则点B的对应点B′的坐标为 （6，2） ．
【分析】作BE⊥OA于E，根据直角三角形的性质、锐角三角函数的定义求出点B的坐标，再根据位似变换的性质解答即可．
【解答】解：作BE⊥OA于E，
则∠BEO＝90°，
∵∠ABO＝90°，∠BOA＝30°，
∴OB＝OA•cs30°＝4×＝2，
∴BE＝OB＝，OE＝OB•cs30°＝2×＝3，
∴点B的坐标为：（3，），
∵以点O为位似中心，在第一象限内将△AOB放大，使相似比为2：1，
∴点B的对应点B'的坐标为：（3×2，×2），即（6，2），
故答案为：（6，2）．
12．（2022•朝阳区校级模拟）如图，在平面直角坐标系中，A、B两点的坐标分别为A（﹣1，2）、B（0，2），C、D两点的坐标分别为C（0，﹣1）、D（2，﹣1）．若线段AB和线段CD是位似图形，且位似中心在y轴上，则位似中心的坐标为 （0，1） ．
【分析】连接AD交BC于E，根据坐标与图形性质分别求出AB、CD、BC，根据平行线的性质列出比例式，求出BE，进而求出OE，得到答案．
【解答】解：连接AD交BC于E，则点E为位似中心，
∵A（﹣1，2）、B（0，2），C（0，﹣1）、D（2，﹣1）．
∴AB＝1，CD＝2，BC＝3，
∵线段AB和CD是位似图形，
∴AB∥CD，
∴＝，即＝，
解得BE＝1，
∴OE＝OB﹣BE＝1，
∴位似中心点E的坐标为（0，1），
故答案为：（0，1）．
13．（2022•潍坊）《墨子•天文志》记载：“执规矩，以度天下之方圆．”度方知圆，感悟数学之美．如图，正方形ABCD的面积为4，以它的对角线的交点为位似中心，作它的位似图形A'B'C'D'，若A'B'：AB＝2：1，则四边形A'B'C'D'的外接圆的周长为 4π ．
【分析】如图，连接B′D′．利用相似多边形的性质求出正方形A′B′C′D′的面积，求出边长，再求出B′D′可得结论．
【解答】解：如图，连接B′D′．设B′D′的中点为O．
∵正方形ABCD∽正方形A′B′C′D′，相似比为1：2，
又∵正方形ABCD的面积为4，
∴正方形A′B′C′D′的面积为16，
∴A′B′＝A′D′＝4，
∵∠B′A′D′＝90°，
∴B′D′＝A′B′＝4，
∴正方形A′B′C′D′的外接圆的周长＝4π，
故答案为：4π．
14．（2022•青羊区校级模拟）如图，小“鱼”与大“鱼”是位似图形，如果小“鱼”上一个“顶点”的坐标为（a，﹣b），那么大“鱼”上对应“顶点”的坐标为 （﹣2a，2b） ．
【分析】先找一对应点是如何变化，那么所求点也符合这个变化规律．
【解答】解：小鱼最大鱼翅的顶端坐标为（5，3），大鱼对应点坐标为（﹣10，﹣6）；
小“鱼”上一个“顶点”的坐标为（a，﹣b），那么大“鱼”上对应“顶点”的坐标为（﹣2a，2b）．
故答案为：（﹣2a，2b）．
15．（2015秋•乐亭县期中）如图，在平面直角坐标系中，△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形，且点B（3，1），B′（6，2）．
（1）若点A（，3），则A′的坐标为 （5，6） ；
（2）△ABC与△A′B′C′的相似比等于 1：2 ；
（3）若△ABC的面积为m，则△A′B′C′的面积＝ 4m ．
【分析】（1）利用点B（3，1），B′（6，2）即可得出位似比进而得出A′的坐标；
（2）利用对应点坐标的变化即可得出相似比；
（3）利用位似图形面积比等于相似比的平方进而得出答案．
【解答】解：（1）∵△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形，且点B（3，1），B′（6，2），
∴若点A（，3），则A′的坐标为：（5，6）；
故答案为：（5，6）；
（2）∵△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形，且点B（3，1），B′（6，2），
∴△ABC与△A′B′C′的相似比等于：1：2；
故答案为：1：2；
（3）∵△ABC与△A′B′C′的相似比等于：1：2，
∴若△ABC的面积为m，则△A′B′C′的面积＝4m．
故答案为：4m．
16．（2019•本溪二模）如图，在平面直角坐标系中，正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形，且相似比为，点A1，A2，A3，…在x轴上，延长A3C2交射线OB1于点B3，以A3B3为边长作正方形A3B3C3A4；延长A4C3交射线OB1于点B4，以A4B4为边长作正方形A4B4C4A5…，分别连接B1C2，B2C3，B3C4，…，得到△B1B2C2，△B2B3C3，△B3B4C4，…按照此规律继续下去，若OA1＝2，则△B2018B2019C2019的面积为 42018 ．
【分析】根据已知条件得到OA1B1∽△OA2B2，求得＝＝，得到OA2＝4求得B1B2＝B1C1＝2，得到OA2＝A2B2＝B2C2＝4，过C2作C2H⊥B2B3，根据等腰直角三角形的性质得到C2H＝B2C2＝2，根据三角形的面积公式即可得到结论．
【解答】解：∵正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形，且相似比为，
∴＝，
∵A1B1⊥x轴，A2B2⊥x轴，
∴A1B1∥A2B2，
∴OA1B1∽△OA2B2，
∴＝＝，
∵OA1＝2，
∴OA2＝4，
∴A1A2＝2，
∴B1C1＝A1A2＝2，
∴B1B2＝B1C1＝2，
∵OA1＝A1A2＝A1B1＝2，
∴∠B1OA1＝45°，
∴OA2＝A2B2＝B2C2＝4，
过C2作C2H⊥B2B3于H，
∴C2H＝B2C2＝2，
∴△B1B2C2的面积＝B1B2•C2H＝×＝4＝41，
同理，△B2B3C3的面积＝×4×4＝16＝42，
△B3B4C4的面积＝88＝64＝43…，
∴△B2018B2019C2019的面积＝42018，
故答案为：42018．
三．解答题（共6小题）
17．（2022秋•天桥区校级月考）如图，在平面直角坐标系中，O是坐标原点，以点O为位似中心，△A1B1C1和△ABC相似比为2：1，在网格中画出新图象△A1B1C1，若每个小正方形边长均为1，请写出A1，B1，C1的坐标．
【分析】利用位似变换的性质分别作出A，B，C的对应点A1，B1，C1即可．
【解答】解：如图，△A1B1C1即为所求，A1（0，8），B1（6，6），C1（6，2）．
18．（2022•兴庆区校级三模）如图，在平面直角坐标系中，△ABC和△A1B1C1关于点E成中心对称，
（1）在图中标出点E，且点E的坐标为 （0，﹣1） ；
（2）点P（a，b）是△ABC边AB上一点，△ABC经过平移后点P的对应点P′的坐标为（a﹣6，b+2），请画出上述平移后的△A2B2C2，此时A2的坐标为 （﹣3，4） ，C2的坐标为 （﹣2，2） ；
（3）若△A1B1C1和△A2B2C2关于点F成位似三角形，则点F的坐标为 （﹣3，0） ．
【分析】（1）根据中心对称的性质，任何一对对应点连线的中点即为对称中心E；
（2）将△ABC向左平移6个单位长度，再向上平移2个单位长度，即可得到△A2B2C2，根据平移的规律，可分别写出点A2和C2的坐标；
（3）根据位似三角形的定义求出点F的坐标．
【解答】解：（1）如图，线段BB1的中点即为点E，
∵B（1，1），B1（﹣1，﹣3）
∴E（0，﹣1）；
（2）如图，
∵点P（a，b）是△ABC边AB上一点，△ABC经过平移后点P的对应点P′的坐标为（a﹣6，b+2），
又∵A（3，2），C（4，0），
∴A2（﹣3，4），C2（﹣2，2）；
（3）∵对应顶点A1A2与B1B2的连线交于点（﹣3，0），
∴F（﹣3，0）．
19．（2019春•路北区期末）如图，在平面直角坐标系xOy中，长方形ABCD的四个顶点分别为（1，1），（1，2），（﹣2，2），（﹣2，1）．对该长方形及其内部的每一个点都进行如下操作：把每个点的横坐标都乘以同一个实数a，纵坐标都乘以3，再将得到的点向右平移m（m＞0）个单位，向下平移2个单位，得到长方形A′B′C′D′及其内部的点，其中点A，B，C，D的对应点分别为A′，B′，C′，D′．
（1）点A′的横坐标为 a+m （用含a，m的式子表示）．
（2）点A′的坐标为（3，1），点C′的坐标为（﹣3，4），
①求a，m的值；
②若对长方形ABCD内部（不包括边界）的点E（0，y）进行上述操作后，得到的对应点E′仍然在长方形ABCD内部（不包括边界），求y的取值范围．
【分析】（1）根据点A′的坐标的横坐标、纵坐标填空；
（2）①根据平移规律得到：a+m＝3，﹣2a+m＝﹣3，联立方程组，求解；
②可知无论y取何值，点E'一定落在AB上．
【解答】解：（1）点A′的横坐标为 a+m
故答案是：a+m．
（2）①由A（1，1），A′（3，1），可得a+m＝3．①
由C（﹣2，2），（﹣3，4），可得﹣2a+m＝﹣3．②
由①，②得
解得
∴a＝2，m＝1．
②根据题意，得E'（1，3y﹣2）．可知无论y取何值，点E'一定落在AB上．所以不存在满足题意的y值．
20．（2021秋•乐平市校级月考）如图所示，由位似的正△A1B1C1，正△A2B2C2，正△A3B3C3，…正△AnBn∁n组成的相似图形，其中第一个△A1B1C1的边长为1，点O是B1C1中点，A2是OA1的中点，A3是OA2的中点…An是OAn﹣1的中点，顶点B2，B3，…，Bn．C2，C3，…，∁n都在B1C1边上．
（1）试写出△A10B10C10和△A7B7C7的相似比和位似中心；
（2）求出第n个三角形△AnBn∁n（n≥2）的周长．
【分析】（1）由于点O是B1C1中点，A2是OA1的中点，则可得到正△A2B2C2的边长为，正△A3B3C3的边长为（）2，利用此规律可得第n个三角形△AnBn∁n（n≥2）的边长为（）n﹣1，所以正△A10B10C10的边长为（）9，正△A7B7C7的边长为（）6，然后根据对应边的比等于相似比即可得到△A10B10C10和△A7B7C7的相似比，再根据位似的定义确定位似中心；
（2）利用第n个三角形△AnBn∁n（n≥2）的边长为（）n﹣1易得第n个三角形△AnBn∁n（n≥2）的周长．
【解答】解：（1）∵△A1B1C1的边长为1，点O是B1C1中点，A2是OA1的中点，
∴正△A2B2C2的边长为，
正△A3B3C3的边长为（）2，
正△A10B10C10和的边长为（）9，正△A7B7C7的边长为（）6，
∴正△A10B10C10和正△A7B7C7的相似比＝＝；它们的位似中心为点O；
（2）∵第n个三角形△AnBn∁n（n≥2）的边长为（）n﹣1，
∴第n个三角形△AnBn∁n（n≥2）的周长为．
21．（2020•如皋市一模）如图，△ABC中，P′是边AB上一点，四边形P'Q'M'N'是正方形，点Q'，M'在边BC上，点N′在△ABC内．连接BN′，并延长交AC于点N，过点N作NM⊥BC于点M，NP⊥MN交AB于点P，PQ⊥BC于点Q．
（1）求证：四边形PQMN为正方形；
（2）若∠A＝90°，AC＝1.5m，△ABC的面积＝1.5m2．求PN的长．
【分析】（1）易得四边形PQMN为矩形，再利用平行线分线段成比例得到＝＝，加上P′N′＝M′N′，所以PN＝MN，从而可判断四边形PQMN为正方形；
（2）解：作AD⊥BC于D，AD交PN于E，如图，利用三角形面积公式先计算出AB＝2，再利用勾股定理计算出BC＝2.5，接着利用面积法求出AD＝，设PN＝x，则PQ＝DE＝x，AE＝﹣x，证明△APN∽△ABC，然后利用相似比得到＝，最后利用相似比求出x即可．
【解答】（1）证明：∵NM⊥BC，NP⊥MN，PQ⊥BC，
∴四边形PQMN为矩形，
∵四边形P'Q'M'N'是正方形，
∴PN∥P′N′，
∴＝，
∵MN∥M′N′，
∴＝，
∴＝，
而P′N′＝M′N′，
∴PN＝MN，
∴四边形PQMN为正方形；
（2）解：作AD⊥BC于D，AD交PN于E，如图，
∵△ABC的面积＝1.5，
∴AB•AC＝1.5，
∴AB＝2，
∴BC＝＝2.5，
∵BC•AD＝1.5，
∴AD＝＝，
设PN＝x，则PQ＝DE＝x，AE＝﹣x，
∵PN∥BC，
∴△APN∽△ABC，
∴＝，即＝，解得x＝，
即PN的长为m．
22．（2014秋•北京校级月考）如图1，给定锐角三角形ABC，小明希望画正方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上，他发现直接画图比较困难，于是他先画了一个正方形HIJK，使得点H，I位于射线BC上，K位于射线BA上，而不要求J必须位于AC上．这时他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG．
阅读以上材料，回答小明接下来研究的以下问题：
（1）如图2，给定锐角三角形ABC，画出所有长宽比为2：1的长方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上．
（2）已知三角形ABC的面积为36，BC＝12，在第（1）问的条件下，求长方形DEFG的面积．
【分析】（1）如图2，先画长方形HIJK，使得HI＝2HK，并且H，I位于射线BC上，K位于射线BA上，连接BJ并延长交AC于点F，再将长方形HIJK通过放大可得到满足要求的长方形DEFG；如备用图，先画长方形HIJK，使得HK＝2HI，并且H，I位于射线BC上，K位于射线BA上，连接BJ并延长交AC于点F，再将长方形HIJK通过放大可得到满足要求的长方形DEFG；
（2）作△ABC的高AM，交GF于N．由三角形ABC的面积为36，求出AM＝6．再设AN＝x，由GF∥BC，得出△AGF∽△ABC，根据相似三角形对应高的比等于相似比列出比例式＝，由此求出x的值，进而求解即可．
【解答】解：（1）如图2与备用图1，长方形DEFG即为所求作的图形；
（2）在长方形DEFG中，如果DE＝2DG，如备用图2，作△ABC的高AM，交GF于N．
∵三角形ABC的面积＝BC•AM＝×12AM＝36，
∴AM＝6．
设AN＝x，则MN＝6﹣x，DG＝MN＝6﹣x，DE＝GF＝2（6﹣x）＝12﹣2x．
∵GF∥BC，
∴△AGF∽△ABC，
∴＝，
∴＝，
解得x＝3，
∴DG＝6﹣x＝3，DE＝2DG＝6，
∴长方形DEFG的面积＝6×3＝18；
在长方形DEFG中，如果DG＝2DE，同理求出x＝，
∴DG＝6﹣x＝，DE＝DG＝，
∴长方形DEFG的面积＝×＝．
故长方形DEFG的面积为18或．