苏科版数学九年级上册期末专题训练专题08 三角形内切圆与内心（2份，原卷版+解析版）

这是一份苏科版数学九年级上册期末专题训练专题08 三角形内切圆与内心（2份，原卷版+解析版），文件包含苏科版数学九年级上册期末专题训练专题08三角形内切圆与内心原卷版doc、苏科版数学九年级上册期末专题训练专题08三角形内切圆与内心解析版doc等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。
1．（2020秋•赣榆区期末）Rt△ABC中，∠C＝90°，AB＝5，内切圆半径为1，则三角形的周长为（ ）
A．12B．13C．14D．15
【分析】作出图形，设内切圆⊙O与△ABC三边的切点分别为D、E、F，连接OE、OF可得四边形OECF是正方形，根据正方形的四条边都相等求出CE、CF，根据切线长定理可得AD＝AF，BD＝BE，从而得到AF+BE＝AB，再根据三角形的周长的定义解答即可．
【解答】解：如图，设内切圆⊙O与△ABC三边的切点分别为D、E、F，连接OE、OF，
∵∠C＝90°，
∴四边形OECF是正方形，
∴CE＝CF＝1，
由切线长定理得，AD＝AF，BD＝BE，
∴AF+BE＝AD+BD＝AB＝5，
∴三角形的周长＝5+5+1+1＝12．
故选：A．
【点评】本题考查了三角形的内切圆与内心，切线长定理，作辅助线构造出正方形是解题的关键，难点在于将三角形的三边分成若干条小的线段，作出图形更形象直观．
2．（2020秋•鼓楼区期末）如图所示，在4×4的网格中，A，B，C，D，O均在格点上，则点O是（ ）
A．△ACD的外心B．△ACD的内心C．△ABC的内心D．△ABC的外心
【分析】根据网格利用勾股定理得出OA＝OD＝OC，进而判断即可．
【解答】解：由勾股定理可知：
OA＝OD＝OC，
所以点O是△ACD的外心，
故选：A．
【点评】此题考查三角形的外接圆与外心问题，关键是根据勾股定理得出OA＝OD＝OC．
3．（2021秋•镇江期末）如图，在矩形ABCD中，AB＝8，BC＝6，点E、F分别是AD、BC的中点，点P在线段EF上，△PAB内切圆半径的最大值是（ ）
A．1B．C．D．
【分析】由三角形APB的面积为12，可知AP+BP最小时，r有最大值，连接CA与EF交于点P'，求出AC＝10，由三角形面积公式可得出答案．
【解答】解：∵点E、F分别是AD、BC的中点，四边形ABCD是矩形，
∴EF∥AB，
∵P在EF上，AB＝8，BC＝6，
∴S△PAB8×3＝12，
设△PAB内切圆半径是r，
∵S△PAB（AP+PB+AB）•r＝12，
∴AP+BP最小时，r有最大值，
如图，F是BC的中点，所以点B关于EF的对称点是C点，连接CA与EF交于点P'，
∵AP+BP＝AP+CP≥CA，
∴此时CA即为AP+BP最小值，
∵AB＝8，AD＝6，
∴AC10，
∴AP+BP最小值为10，
∴PA＝PB＝5，
∴8×r＝12，
解得r．
故选：D．
【点评】本题考查矩形的性质，勾股定理，直角三角形的性质，轴对称求最短距离；能够将AP+BP最小值转化为CA的长是解题的关键．
4．（2019秋•海陵区校级期末）下列说法正确的是（ ）
A．三角形的外心一定在三角形的外部
B．三角形的内心到三个顶点的距离相等
C．外心和内心重合的三角形一定是等边三角形
D．直角三角形内心到两锐角顶点连线的夹角为125°
【分析】利用三角形内心以及三角形外心的性质判断得出即可．
【解答】解：A、三角形的外心不一定在三角形的外部，错误；
B、三角形的内心到三个边的距离相等，错误；
C、外心和内心重合的三角形一定是等边三角形，正确；
D、直角三角形内心到两锐角顶点连线的夹角为135°，错误；
故选：C．
【点评】此题主要考查了三角形内外心的区别，正确把握相关性质是解题关键．
二．填空题（共4小题）
5．（2021秋•邗江区期末）如图所示，点O是△ABC的内切圆的圆心，若∠BAC＝76°，则∠BOC的度数为 128° ．
【分析】由点O是△ABC的内切圆的圆心，可得∠OBC∠ABC，∠OCB∠ACB，又由∠BAC＝76°，可求得∠ABC+∠ACB的度数，再利用三角形内角和定理即可求得答案．
【解答】解：∵点O是△ABC的内切圆的圆心，
∴BO、CO分别平分∠ABC、∠ACB，
∴∠OBC∠ABC，∠OCB∠ACB，
∵∠BAC＝76°，
∴∠ABC+∠ACB＝180°﹣∠BAC＝104°，
∴∠BOC＝180°﹣（∠OBC+∠OCB）＝180°（∠ABC+∠ACB）＝180°104°＝128°．
故答案为：128°．
【点评】本题考查了三角形的内切圆的性质与三角形内角和定理．注意掌握数形结合思想与整体思想的应用．
6．（2020秋•滨湖区期末）设两直角边分别为3、4的直角三角形的外接圆和内切圆的半径长分别为R和r，则R﹣r＝ 1.5 ．
【分析】利用三角形的外心与内心的性质即可进行计算．
【解答】解：因为直角三角形的外接圆半径等于斜边长的一半，
所以R2.5；
如图，
若Rt△ABC的边AC＝3，BC＝4，
根据勾股定理，得AB5，
其内切圆⊙O分别切AB、BC、AC于D、E、F．
设OE＝OF＝OD＝r，
∴S△ABC＝S△AOB+S△BOC+S△AOC，
即AC•BCAB•ODBC•OEAC•OF，
3×45×r4×r3×r，
6r（5+4+3），
6＝6r，
∴r＝1，
则R﹣r＝2.5﹣1＝1.5．
故答案为：1.5．
【点评】本题考查了三角形的内切圆与内心，三角形的外接圆与外心关系，牢记这些定义和计算方法是解答本题的关键．
7．（2019秋•鼓楼区期末）已知三点A（0，0），B（5，12），C（14，0），则△ABC内心的坐标为 （6，4） ．
【分析】作BQ⊥OC，由题意可得BQ＝12，根据勾股定理分别求出OB的长，利用面积法可得△ABC内切圆半径，设AD＝AE＝x，则CD＝CF＝14﹣x，BE＝BF＝13﹣x，由BC＝BF+CF列方程，解之求出x的值，从而得出点P的坐标，即可得出答案．
【解答】解：如图，过点B作BQ⊥OA于点Q，连接PA，PB，PC，
则OQ＝5，BQ＝12，
∴OB13，CQ＝AC﹣AQ＝14﹣5＝9，
∴BC15，
设⊙P的半径为r，
过点P作PD⊥AC于D，PF⊥BC于F，PE⊥OB于E，
S△ABC
则r4，
设AD＝AE＝x，则CD＝CF＝14﹣x，BE＝BF＝13﹣x，
∵BC＝BF+CF，
∴13﹣x+14﹣x＝15，
解得：x＝6，
∴点P的坐标为（6，4）．
故答案为：（6，4）．
【点评】本题主要考查勾股定理、三角形的内切圆的性质及切线长定理，根据面积法及切线长定理求出点P的坐标是解题的关键．
8．（2021秋•鼓楼区期末）△ABC中，AB＝AC＝13，BC＝24，点I是△ABC的内心，点O是△ABC的外心，则OI＝ 14.3 ．
【分析】设BC边的中点为D，连接AD，根据等腰三角形的性质得到AD⊥BC，∠DAB＝∠CAD，得到内心I和外心O都在直线AD上，根据勾股定理得到AD＝5，设△ABC的内切圆半径为r，外接圆半径为R，则IO＝DI+OD，根据勾股定理列方程得到R＝16.9，求得OD＝11.9，根据三角形的面积公式得到r＝2.4，于是得到结论．
【解答】解：设BC边的中点为D，连接AD，
∵AB＝AC＝13，
∴AD⊥BC，∠DAB＝∠CAD，
∵点O为△ABC的外心，点I为△ABC的内心，
∴内心I和外心O都在直线AD上，
∵AB＝AC＝13，BC＝24，
∴BD＝CD＝12，
∴AD5，
设△ABC的内切圆半径为r，外接圆半径为R，则IO＝DI+OD，
连接OB，在Rt△ODB中，OD＝R﹣5，OB＝R，DB＝12，
由勾股定理得（R﹣5）2+122＝R2，
∴R＝16.9，
∴OD＝AO﹣AD＝16.9﹣5＝11.9，
∵S△ABCBC•AD（AB+BC+AC）•r，
∴r2.4，
∴r＝DI＝2.4，
∴IO＝DI+OD＝2.4+11.9＝14.3．
故答案为：14.3．
【点评】本题考查了三角形的内切圆与内心，等腰三角形的性质，勾股定理，三角形面积的计算，正确作出辅助线是解题的关键．
三．解答题（共4小题）
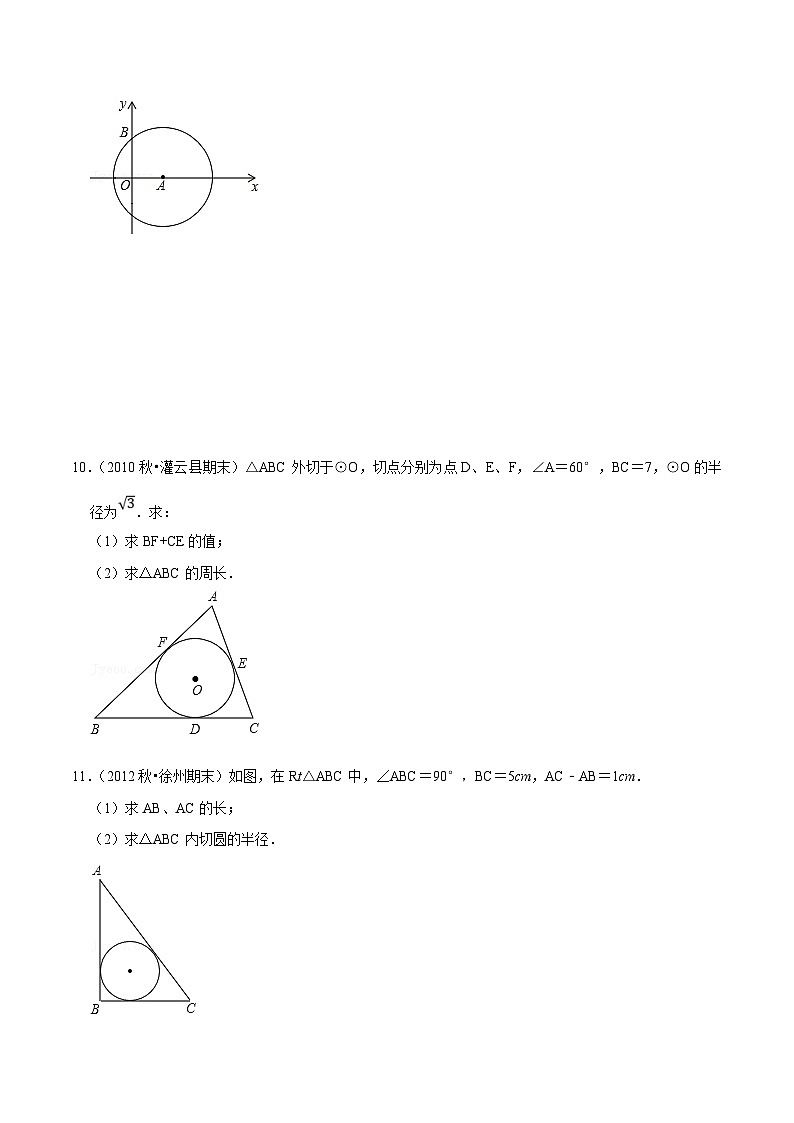
9．（2018秋•武进区校级期末）如图，在平面直角坐标系中，以A（3，0）为圆心，5为半径作⊙A，与y轴的正半轴交于点B．
（1）点B的坐标为 （0，4） ；
（2）△AOB的内切圆半径为 1 个单位长度；
（3）将⊙A在平面直角坐标系内平移，使其与x轴、y轴都相切，记平移后的圆的圆心为A1，则AA1 为或 个单位长度．
【分析】（1）连接AB，利用勾股定理计算出OB即可得到B点坐标；
（2）利用直角三角形内切圆的半径（a、b为直角边，c为斜边）进行计算即可；
（3）根据切线的性质可判定A1的坐标为（5，5）或（﹣5，5）或（﹣5，﹣5）或（5，﹣5），然后利用两点间的距离公式计算AA1的长即可．
【解答】解：（1）连接AB，如图，
在Rt△OAB中，OB4，
∴B点坐标为（0，4）；
（2）△AOB的内切圆半径1；
（3）∵⊙A1与x轴、y轴都相切，
而⊙A1的半径为5，
∴A1的坐标为（5，5）或（﹣5，5）或（﹣5，﹣5）或（5，﹣5），
若A1的坐标为（5，5），则AA1；
若A1的坐标为（﹣5，5），则AA1；
若A1的坐标为（﹣5，﹣5），则AA1；
若A1的坐标为（5，﹣5），则AA1；
综上所述，AA1为或个单位长度．
故答案为（0，4）；1；为或．
【点评】本题考查了三角形内切圆与内心：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了切线的性质．
10．（2010秋•灌云县期末）△ABC外切于⊙O，切点分别为点D、E、F，∠A＝60°，BC＝7，⊙O的半径为．求：
（1）求BF+CE的值；
（2）求△ABC的周长．
【分析】（1）根据切线长定理得到BF＝BD，CE＝CD，代入求出即可；
（2）根据切线长定理得到AE＝AF，求出∠OAE＝30°，根据含30度得直角三角形和勾股定理求出OA、AE，即可求出答案．
【解答】解：（1）∵△ABC外切于⊙O，切点分别为点D、E、F，
∴BF＝BD，CE＝CD，
∴BF+CE＝BD+CD＝BC＝7，
答：BF+CE的值是7．
（2）连接OE、OF、OA，
∵△ABC外切于⊙O，切点分别为点D、E、F，
∴∠OEA＝90°，∠OAE∠BAC＝30°，
∴OA＝2OE＝2，
由勾股定理得：AE＝AF3，
∴△ABC的周长是AB+BC+AC＝AF+AE+CE+BF+BC＝7+7+3+3＝20，
答：△ABC的周长是20．
【点评】本题主要考查对勾股定理，含30度角的直角三角形，切线长定理，三角形的内切圆与内心等知识点的理解和掌握，熟练地运用这些性质进行推理是解此题的关键．
11．（2012秋•徐州期末）如图，在Rt△ABC中，∠ABC＝90°，BC＝5cm，AC﹣AB＝1cm．
（1）求AB、AC的长；
（2）求△ABC内切圆的半径．
【分析】（1）设AB＝xcm，则AC＝（x+1）cm，根据勾股定理得出方程（x+1）2﹣x2＝52，求出x即可；
（2）设内切圆的半径为y，根据三角形面积公式得出S△ABC5×125r12r13r，求出即可．
【解答】解：（1）设AB＝xcm，则AC＝（x+1）cm，
∵在Rt△ABC中，由勾股定理得：AC2﹣AB2＝BC2，
∴（x+1）2﹣x2＝52，
解得：x＝12，
即AB＝12cm，AC＝13cm；
（2）
连接AO、BO、CO、OD、OE、OF，
设内切圆的半径为y，根据题意，得S△ABC5×125r12r13r，
解得：r＝2，
即所求内切圆的半径为2cm．
【点评】本题考查了三角形的面积，三角形的内切圆和内心，勾股定理的应用，用了方程思想．
12．（2010秋•海陵区期末）如图，I是△ABC的内心，∠BAC的平分线与△ABC的外接圆相交于点D，与BC相交于点E．
（1）写出图中与△CAE相似的所有三角形；
（2）求证：DI＝DB；
（3）求证：DI2＝DE•DA．
【分析】（1）根据同弧所对的圆周角相等，得∠C＝∠D，∠CAE＝∠DBE，再由角平分线定义，则△DBE∽△ABC，△DAB∽△ABC；
（2）连接BI，CI，CD，求证△BCD为等腰三角形，再利用BI为∠ABC平分线，求证△DBI为等腰三角形，利用等量代换即可证明；
（3）证△DBE∽△DAB，得DB2＝DE•DA，再由（2）得DI2＝DE•DA．
【解答】（1）解：与△CAE相似的所有三角形：△DBE，△DAB；
∵∠C＝∠D，∠CAE＝∠DBE，
∴△DBE∽△CAE；
∵∠C＝∠D，AD是∠BAC的平分线，
∴∠BAD＝∠EAC，
∴△DAB∽△CAE；
（2）证明：连接BI，CI，CD，
∵I为内心，
∴AI为∠BAC角平分线，
BI为∠ABC平分线，
∴∠ABI＝∠CBI，∠BAD＝∠DAC，
∵∠BID＝∠ABI+∠BAI，
∠CBD＝∠DAC＝∠BAI，
∴∠BID＝∠CBI+∠CBD＝∠DBI，
∴△DBI为等腰三角形，
∴DB＝DI；
（3）证明：∵∠DBE＝∠CAD，∠BAE＝∠CAE，
∴∠BAE＝∠EBD，
∴△DBE∽△DAB，
∴，
∴DB2＝DE•DA，
又∵DB＝DI（已证），
∴DI2＝DE•DA．
【点评】本题考查了三角形的相似和性质以及三角形的内切圆与内心，证明此题的关键是连接BI，CI，CD，求证△BCD为等腰三角形，再利用BI为∠ABC平分线，求证△DBI为等腰三角形．
一．选择题（共4小题）
1．（2022秋•鼓楼区期中）如图，在一张Rt△ABC纸片中，∠ACB＝90°，BC＝3，AC＝4，⊙O是它的内切圆．小明用剪刀沿着⊙O的切线DE剪下一块三角形ADE，则△ADE的周长为（ ）
A．4B．5C．6D．8
【分析】设△ABC的内切圆切三边于点F，H，G，连接OF，OH，OG，得四边形OHCG是正方形，由切线长定理可知：AF＝AG，根据DE是⊙O的切线，可得MD＝MF，EM＝EG，根据勾股定理可得AB＝5，再求出内切圆的半径（AC+BC﹣AB）＝1，进而可得△ADE的周长．
【解答】解：如图，设△ABC的内切圆切三边于点F，H，G，连接OF，OH，OG，
∴四边形OHCG是正方形，
由切线长定理可知：AF＝AG，
∵DE是⊙O的切线，
∴MD＝MF，EM＝EG，
∵∠ACB＝90°，BC＝3，AC＝4，
∴AB5，
∵⊙O是△ABC的内切圆，
∴内切圆的半径（AC+BC﹣AB）＝1，
∴CG＝1，
∴AG＝AC﹣CG＝4﹣1＝3，
∴△ADE的周长＝AD+DE+AE＝AD+DF+EG+AE＝AF+AG＝2AG＝6．
故选：C．
【点评】本题考查了三角形的内切圆与内心，勾股定理，切线的性质，解决本题的关键是掌握切线的性质．
2．（2022秋•海陵区校级期中）如图，△ABC中，∠C＝90°，AC＝4，BC＝3，I为△ABC的内心，ID∥AC，IE∥BC，则△IDE的周长为（ ）
A．6B．5C．4.8D．4
【分析】先解直角三角形得到AB＝5，连接IA、IB，如图，利用三角形的内心的性质得到∠1＝∠2，再证明∠2＝∠3得到DA＝DI，同理可得EI＝EB，所以△IDE的周长＝AB＝5．
【解答】解：∵∠C＝90°，AC＝4，BC＝3，
∴AB5，
连接IA、IB，如图，
∵I为△ABC的内心，
∴AI平分∠CAB，
即∠1＝∠2，
∵ID∥AC，
∴∠1＝∠3，
∴∠2＝∠3，
∴DA＝DI，
同理可得EI＝EB，
∴△IDE的周长＝ID+DE+IE＝DA+DE+EB＝AB＝5．
故选：B．
【点评】本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．
3．（2022秋•鼓楼区校级月考）如图，已知AB是⊙O的直径，CD，CB是⊙O的切线，D，B为切点，OC交⊙O于点E，AE的延长线交BC于点F，连接AD，BD，给出以下四个结论：①AD∥OC；②E为△CDB的内心；③FC＝FE．其中正确的结论是（ ）
A．①②B．②③C．①③D．①②③
【分析】①利用切线长定理和等腰三角形三线合一证明即可；
②由垂径定理得，再由切线性质推角相等，进一步证明DE平分∠CDB，BE平分∠CBD，最后证点E为△CDB的内心；
③利用①的结论AD∥OC推∠NDA＝∠NCM，再根据切线性质推角相等，等量代换后推∠MCB＝∠DBA，由不一定等于，推角也不一定相等．
【解答】解：①∵AB为⊙O的直径，
∴∠ADB＝90°，
∵CD、CB为⊙O的切线，
∴CD＝CB，CO平分∠DCB，
∴CO⊥BD，
∴∠OHB＝90°，
∴∠OHB＝∠ADB，
∴AD∥OC，故①正确；
②连接DE、BE，
∵CD为⊙O的切线，
∴∠CDE＝∠DAE，
∵CO⊥BD，
∴，
∴∠DAF＝∠EDB，
∴∠CDE＝∠EDB，
∴DE平分∠CDB，
同理可证BE平分∠CBD，
∵CO平分∠DCB，
∴点E为△CDB的内心，故②正确；
③∵AD∥OC，
∴∠NDA＝∠NCM．
∵CO平分∠DCB，
∴∠DCM＝∠MCB，
∵CD为⊙O的切线，
∴∠NDA＝∠DBA，
∴∠MCB＝∠DBA，
∵∠CEF＝∠AEM，
不一定等于，
∴∠CFE，∠AGB不一定相等
∴FC、EF也不一定相等，故③不正确，
∴正确的结论是①②．
故选：A．
【点评】本题考查了切线长定理、圆周角的性质定理、外角性质，掌握这些性质定理的综合应用，辅助线的作法是解题关键．
4．（2022•邗江区校级开学）如图，点I和O分别是△ABC的内心和外心，若∠AIB＝125°，则∠AOB的度数为（ ）
A．120°B．125°C．135°D．140°
【分析】根据圆周角定义，以及内心的定义，可以利用∠C表示出∠AIB和∠AOB，即可得到两个角的关系．
【解答】解：∵点O是△ABC的外心，
∴∠AOB＝2∠C，
∴∠C∠AOB，
∵点I是△ABC的内心，
∴∠IAB∠CAB，∠IBA∠CBA，
∴∠AIB＝180°﹣（∠IAB+∠IBA）
＝180°（∠CAB+∠CBA），
＝180°（180°﹣∠C）
＝90°∠C，
∴2∠AIB＝180°+∠C，
∵∠AOB＝2∠C，
∴∠AIB＝90°∠AOB，
∴4∠AIB﹣∠AOB＝360°．
∵∠AIB＝125°，
∴∠AOB＝140°．
故选：D．
【点评】本题考查了三角形的内接圆与内心，三角形的外接圆与外心，解决本题的关键是正确利用∠C表示∠AIB的度数．
二．填空题（共4小题）
5．（2022秋•鼓楼区校级月考）如图，⊙O是等边△ABC的内切圆，切点分别为D、E、F，若等边△ABC的边长为8，则阴影部分的面积是 16π ．
【分析】连接OE、OB、OC，根据等边三角形的性质得∠ABC＝∠ACB＝60°，BC＝8，再利用切线的性质和内心性质得到OE⊥BC，BO平分∠ABC，OC平分∠ACB，从而得到∠OBE＝∠OCE＝30°，再计算OE，然后根据扇形的面积公式，利用S阴影部分＝S△ABC﹣S⊙O＝3S△OBC﹣S⊙O进行计算即可．
【解答】解：如图，连接OE、OB、OC，
∵△ABC为等边三角形，
∴∠ABC＝∠ACB＝60°，BC＝8，
∵⊙O是等边△ABC的内切圆，
∴OE⊥BC，BO平分∠ABC，OC平分∠ACB，
∴∠OBE＝∠OCE＝30°，
∵OB＝OC，OE⊥BC，
∴BE＝CEBC＝4，
在Rt△OBE中，OEBE，
∴S阴影部分＝S△ABC﹣S⊙O
＝3S△OBC﹣S⊙O
＝38π×（）2
＝16π．
故答案为：16π．
【点评】本题考查了三角形的内切圆与内心，等边三角形的性质，切线的性质，解决本题的关键是掌握内心定义．
6．（2022秋•云龙区校级月考）如图，圆O是△ABC的内切圆，若∠ABC＝60°，∠ACB＝50°，则∠BOC＝ 125 °．
【分析】根据三角形的内心的概念得到∠OBC∠ABC＝30°，∠OCB∠ACB＝25°，根据三角形内角和定理计算即可．
【解答】解：∵⊙O是△ABC的内切圆，
∴∠OBC∠ABC60°＝30°，∠OCB∠ACB50°＝25°，
∴∠BOC＝180°﹣∠OBC﹣∠OCB＝125°，
故答案为：125．
【点评】本题考查的是三角形的内切圆与内心，三角形内角和定理，掌握三角形的内心是三角形三个内角角平分线的交点是解题的关键．
7．（2020秋•亭湖区校级月考）如图，已知圆O为Rt△ABC的内切圆，切点分别为D、E、F，且∠C＝90°，AB＝13，BC＝12，则圆O的半径为 2 ．
【分析】设BF＝BD＝x，利用切线长定理，构建方程先求出证明四边形OECF是矩形，推出OE＝CF即可解决问题．
【解答】解：在Rt△ABC中，
∵∠C＝90°，AB＝13，BC＝12，
∴AC5，
∵⊙O为Rt△ABC的内切圆，切点分别为D，E，F，
∴BD＝BF，AD＝AE，CF＝CE，
如图，连接OE，OF，
∵OE⊥AC，OF⊥BC，OE＝OF，
∴∠OEC＝∠C＝∠OFC＝90°，
∴四边形OECF是正方形，
设OE＝OF＝CE＝CF＝x，则AD＝AE＝5﹣x，BF＝BD＝12﹣x，
∵AD+BD＝13，
∴5﹣x+12﹣x＝13，
∴x＝2，
则圆O的半径为2．
故答案为：2．
【点评】本题考查三角形的内切圆与内心，勾股定理，切线长定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
8．（2021秋•高新区校级月考）如图，在△ABC中，I是△ABC的内心，O是AB边上一点，⊙O经过点B且与AI相切于点I，若tan∠BAC，则sin∠ACB的值为 ．
【分析】连接OI，BI，作OE⊥AC，可证△AOD是等腰三角形，然后证明OD∥BC，进而∠ADO＝∠ACB，解三角形AOD即可．
【解答】解：如图，
连接OI并延长交AC于D，连接BI，
∵OI与⊙O相切，
∴AI⊥OD，
∴∠AIO＝∠AID＝90°，
∵I是△ABC的内心，
∴∠OAI＝∠DAI，∠ABI＝∠CBI，
∵AI＝AI，
∴△AOI≌△ADI（ASA），
∴AO＝AD，
∵OB＝OI，
∴∠OBI＝∠OIB，
∴∠OIB＝∠CBI，
∴OD∥BC，
∴∠ADO＝∠C，
作OE⊥AC于E，
∵tan∠BAC，
∴不妨设OE＝24k，AE＝7k，
∴OA＝AD＝25k，
∴DE＝AD﹣AE＝18k，
∴OD30k，
∴sin∠ACB，
故答案是：．
【点评】本题考查课圆的切线性质，内心性质，全等三角形判定和性质，解斜三角形等知识，解决问题的关键是有机地组合条件，发现特殊性．
三．解答题（共4小题）
9．（2022•鼓楼区二模）如图，△ABC内接于⊙O，∠BAC的平分线AF交⊙O于点G，过G作DE∥BC分别交AB，AC的延长线于点D，E．
（1）求证：DE是⊙O的切线；
（2）已知AG＝8，，点I为△ABC的内心，求GI的长．
【分析】（1）连接OG，根据角平分线的定义得到∠BAG＝∠CAG，根据垂径定理得到OG⊥BC，根据平行线的性质得到OG⊥EF，根据切线的判定定理得到结论；
（2）连接BI，BG，根据角平分线定义得到∠BAI＝∠CAI，∠ABI＝∠CBI，推出∠BIG＝∠GBI，得到BG＝IG，根据相似三角形的性质即可得到结论．
【解答】（1）证明：连接OG，
∵∠BAC的平分线AF交⊙O于点G，
∴∠BAG＝∠CAG，
∴，
∴OG⊥BC，
∵DE∥BC
∴OG⊥EF，
∵OG是⊙O的半径，
∴DE为⊙O的切线；
（2）解：连接BI，BG，
∵点I为△ABC的内心，
∴BI平分∠ABC，AG平分∠BAC，
∴∠BAI＝∠CAI，∠ABI＝∠CBI，
∵∠BIG＝∠BAI+∠ABI，∠GBI＝∠GBC+∠CBI，∠GBC＝∠GAC，
∴∠BAI＝∠CBG，
∴∠BIG＝∠GBI，
∴BG＝IG，
∵BC∥DE，
∴△ABF∽△ADG，
∴，
∵AG＝8，
∴AF＝6，
∴FG＝2，
∵∠BGF＝∠AGB，∠GBF＝∠BAG，
∴△BGF∽△AGB，
∴，
∴，
∴BG＝4（负值舍去），
∴GI的长为4．
【点评】本题考查了切线的判定和性质以及相似三角形的判定和性质，是基础知识要熟练掌握．
10．（2022秋•泰州月考）如图，O是△ABC的外心，I是△ABC的内心，连接AI并延长交BC和⊙O于D，E．
（1）求证：EB＝EI；
（2）若AB＝8，AC＝6，BE＝4，求AI的长．
【分析】（1）根据I是△ABC的内心，于是得到AE平分∠CAB，BI平分∠ABC，根据角平分线的定义得到∠BAE＝∠CAE，∠ABI＝∠CBI，根据等腰三角形的性质可得到结论；
（2）连接EC．根据已知条件得到BE＝EC＝4，根据相似三角形的性质即可得到结论．
【解答】（1）证明：∵I是△ABC的内心，
∴AE平分∠CAB，BI平分∠ABC，
∴∠BAE＝∠CAE，∠ABI＝∠CBI，
∵∠BIE＝∠BAE+∠ABI，∠IBE＝∠IBD+∠EBD，
∵∠CBE＝∠CAE，
∴∠BIE＝∠EBI，
∴EB＝EI；
（2）解：连接EC．
∵∠BAE＝∠CAE，
∴，
∴BE＝EC＝4，
∵∠ADB＝∠CDE，∠BAD＝∠DCE，
∴△ADB∽△CDE，
∴2，设DE＝m，CD＝n，则BD＝2m，AD＝2n，
同法可证：△ADC∽△BDE，
∴，
∴，
∴n：m＝3：2，设n＝3k，m＝2k，
∵∠CED＝∠AEC，∠ECD＝∠BAE＝∠CAE，
∴△ECD∽△EAC，
∴EC2＝ED•EA，
∴8＝m•（m+2n），
∴8＝2k（2k+6k）
∴k＝1或﹣1（舍弃），
∴DE＝2，AD＝6，
∴AE＝8，
∵EI＝BE＝4，
∴AI＝AE﹣EI＝4．
【点评】本题考查的是三角形的内切圆与内心，相似三角形的判定和性质等知识，解题的关键是学会利用参数构建方程组解决问题，属于中考压轴题．
11．（2021•武进区校级自主招生）如图，⊙O的内接四边形ABCD中，AC，BD是它的对角线，AC的中点I是△ABD的内心．求证：
（1）OI是△IBD的外接圆的切线；
（2）AB+AD＝2BD．
【分析】（1）根据三角形内心的性质和同弧上圆周角的性质，以及等角对等边即可证得C是△IBD的外心，然后证得OI⊥CI，即可证得OI是△IBD的外接圆的切线；
（2）根据（1）可以得到AI＝CD，AB＝2BF，即可证得．
【解答】解：（1）∵∠CID＝∠IAD+∠IDA，∠CDI＝∠CDB+∠BDI＝∠BAC+∠IDA＝∠IAD+∠IDA
∴∠CID＝∠CDI，
∴CI＝CD．
同理，CI＝CB．
故点C是△IBD的外心．
连接OA，OC，
∵I是AC的中点，且OA＝OC，
∴OI⊥AC，即OI⊥CI．
∴OI是△IBD外接圆的切线．
（2）由（1）可得：
∵AC的中点I是△ABD的内心，
∴∠BAC＝∠CAD
∴∠BDC＝∠DAC＝∠BAC，
又∵∠ACD＝∠DCF，
∴△ADC∽△DFC，
∴，
∵AC＝2CI
∴AC＝2CD
∴AD＝2DF
同理可得：AB＝2BF
∴AB+AD＝2BF+2DF＝2BD．
【点评】本题考查了圆的切线的证明，以及三角形的内心的计算，证得C是△IBD的外心是关键．
12．（2022秋•建湖县期中）如图，I是△ABC的内心，AI的延长线交△ABC的外接圆于点D．
（1）求证：∠BAD＝∠CBD；
（2）求证：BD＝ID；
（3）连接BI、CI，求证：点D是△BIC的外心．
【分析】（1）根据圆周角定理和角平分线的定义即可得到结论；
（2）连接BI，根据I是△ABC的内心可得出∠BAD＝∠CAD，∠ABI＝∠IBC，再由圆周角定理可知∠DBC＝∠DAC，BID是△ABI的一个外角可知∠BID＝∠BAD+∠ABI，故可得出∠IBD＝∠BID，由等腰三角形的性质可得出结论；
（3）连接BI，CI，由AD平分∠BAC，证明BD＝CD，结合（2）可得BD＝CD＝ID，进而可以得点D是△BIC的外心．
【解答】证明：（1）∵点I是△ABC的内心，
∴∠BAD＝∠CAD，
∵∠CBD＝∠CAD，
∴∠BAD＝∠CBD；
（2）如图，连接BI，
∵点I是△ABC的内心，
∴∠BAD＝∠CAD，∠ABI＝∠CBI，
∵∠CBD＝∠CAD，
∴∠BAD＝∠CBD，
∴∠BID＝∠ABI+∠BAD，
∴∠ABI＝∠CBI，∠BAD＝∠CAD＝∠CBD，
∵∠IBD＝∠CBI+∠CBD，
∴∠BID＝∠IBD，
∴ID＝BD；
（3）如图，连接BI、CI，DC，
∵∠BAD＝∠CAD，
∴，
∴BD＝CD，
∴BD＝CD＝ID，
∴点D是△BIC的外心．
【点评】本题考查了三角形的内切圆和内心，三角形的外接圆和外心，垂径定理，圆周角定理，熟练掌握圆周角定理是解此题的关键．