苏科版数学九年级上册期末专题训练专题09 圆的综合练习（2份，原卷版+解析版）

这是一份苏科版数学九年级上册期末专题训练专题09 圆的综合练习（2份，原卷版+解析版），文件包含苏科版数学九年级上册期末专题训练专题09圆的综合练习原卷版doc、苏科版数学九年级上册期末专题训练专题09圆的综合练习解析版doc等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。
1．（2021秋•海陵区校级期末）如图，AB是⊙O的直径，，则∠BAC的度数为（ ）
A．22.5°B．30°C．45°D．67.5°
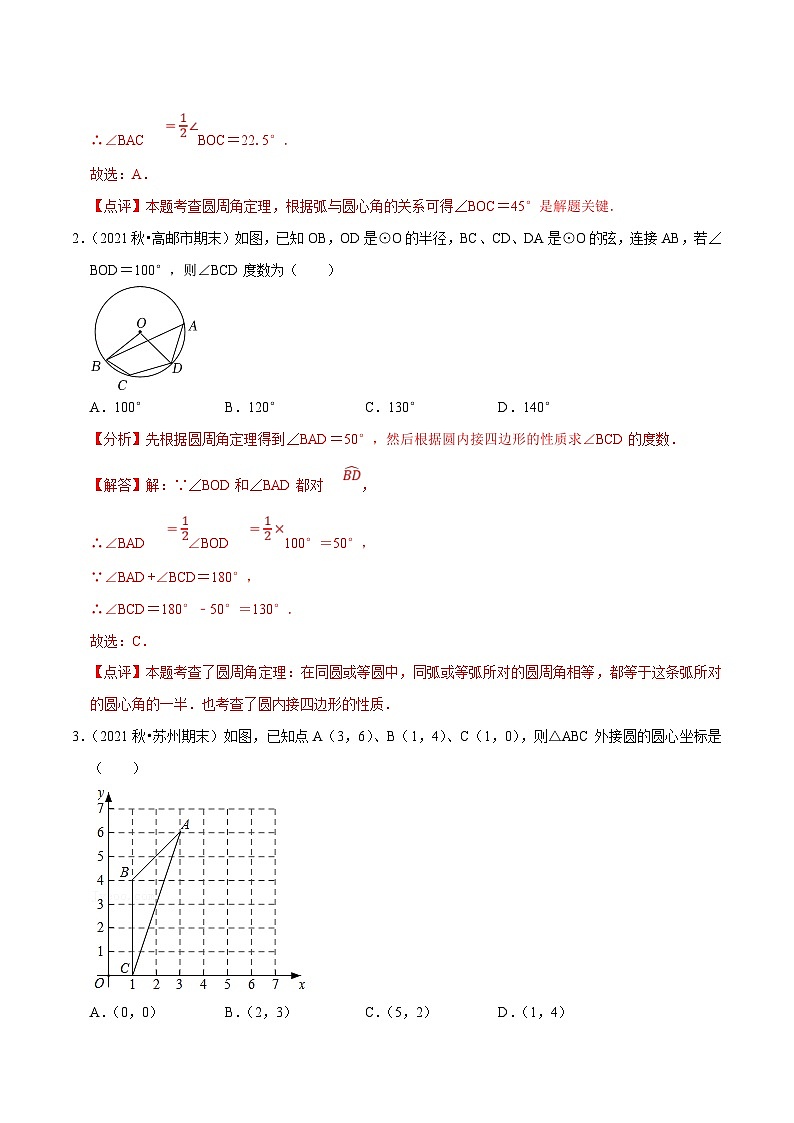
2．（2021秋•高邮市期末）如图，已知OB，OD是⊙O的半径，BC、CD、DA是⊙O的弦，连接AB，若∠BOD＝100°，则∠BCD度数为（ ）
A．100°B．120°C．130°D．140°
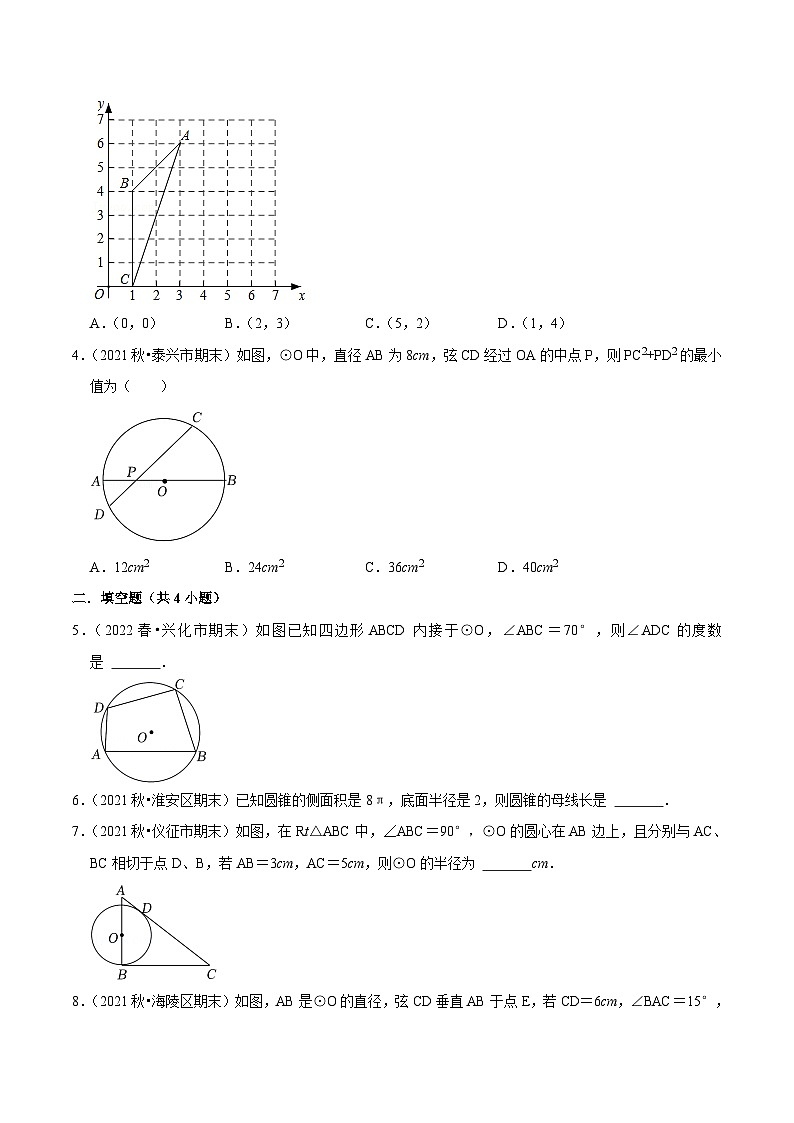
3．（2021秋•苏州期末）如图，已知点A（3，6）、B（1，4）、C（1，0），则△ABC外接圆的圆心坐标是（ ）
A．（0，0）B．（2，3）C．（5，2）D．（1，4）
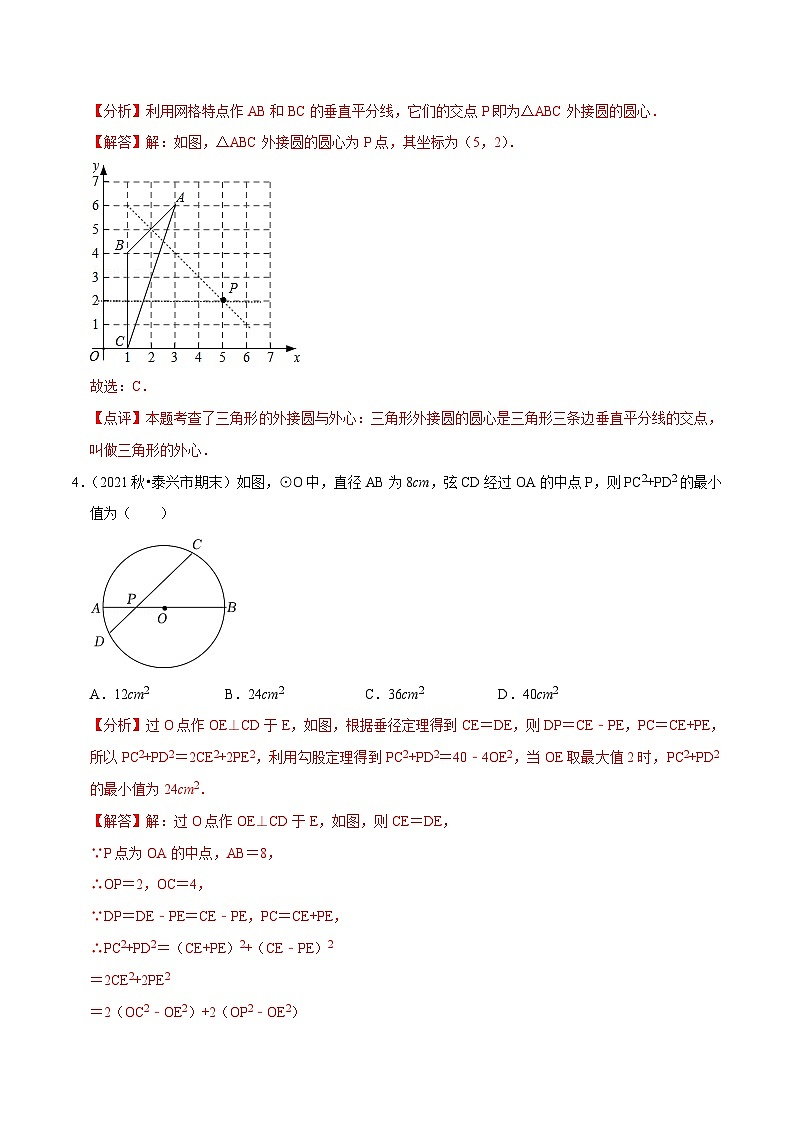
4．（2021秋•泰兴市期末）如图，⊙O中，直径AB为8cm，弦CD经过OA的中点P，则PC2+PD2的最小值为（ ）
A．12cm2B．24cm2C．36cm2D．40cm2
二．填空题（共4小题）
5．（2022春•兴化市期末）如图已知四边形ABCD内接于⊙O，∠ABC＝70°，则∠ADC的度数是 ．
6．（2021秋•淮安区期末）已知圆锥的侧面积是8π，底面半径是2，则圆锥的母线长是 ．
7．（2021秋•仪征市期末）如图，在Rt△ABC中，∠ABC＝90°，⊙O的圆心在AB边上，且分别与AC、BC相切于点D、B，若AB＝3cm，AC＝5cm，则⊙O的半径为 cm．
8．（2021秋•海陵区期末）如图，AB是⊙O的直径，弦CD垂直AB于点E，若CD＝6cm，∠BAC＝15°，则⊙O的半径等于 cm．
三．解答题（共4小题）
9．（2021秋•江都区期末）如图，△ABC内接于⊙O，AB是⊙O的直径，直线l与⊙O相切于点A，在l上取一点D使得DA＝DC，线段DC，AB的延长线交于点E．
（1）求证：直线DC是⊙O的切线；
（2）若BC＝4，∠CAB＝30°，求图中阴影部分的面积（结果保留π）．
10．（2021秋•海州区期末）如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB、AB，∠PBA＝∠C．
（1）求证：PB是⊙O的切线；
（2）连接OP，若OP∥BC，且OP＝8，⊙O的半径为3，求BC的长．
11．（2021秋•玄武区期末）如图，在Rt△ABC中，∠C＝90°，BD平分∠ABC，与AC交于点D，DE⊥DB，垂足为D，与AB交于点E，经过B，D，E三点的⊙O与BC交于点F．
（1）求证AC是⊙O的切线；
（2）若BC＝3，AC＝4，求⊙O的半径．
12．（2021秋•启东市期末）如图，AB为⊙O的直径，C为⊙O上一点，⊙O的切线BD交OC的延长线于点D．
（1）求证：∠DBC＝∠OCA；
（2）若∠BAC＝30°，AC＝2．求CD的长．
一．选择题（共4小题）
1．（2022秋•江阴市校级月考）如图，AB是⊙O的直径，弦CD⊥AB于点E，BE＝2cm，CD＝8cm，则⊙O半径为（ ）
A．2cmB．3cmC．5cmD．8cm
2．（2022秋•玄武区校级月考）如图所示，小区内有个圆形花坛O，点C在弦AB上，AC＝11，BC＝21，OC＝13，则这个花坛的面积为（ ）
A．144πB．256πC．400πD．441π
3．（2022秋•洪泽区校级月考）如图，在平面直角坐标系xOy中，点A在x轴负半轴上，点B在y轴正半轴上，⊙D经过A，B，O，C四点，∠ACO＝120°，AB＝4，则圆心点D的坐标是（ ）
A．B．C．D．
4．（2022秋•宿豫区期中）如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D，与BC相交于点G，则下列结论：①∠BAD＝∠CAD；②若∠BAC＝60°，则∠BEC＝120°；③若点G为BC的中点，则∠BGD＝90°；④BD＝DE．其中一定正确的个数是（ ）
A．1B．2C．3D．4
二．填空题（共4小题）
5．（2022秋•鼓楼区期中）如图，圆的内接五边形ABCDE满足CD＝ED，CD∥AE，∠ABC＝140°，则∠D＝ ．
6．（2022秋•盐都区期中）如图，若Rt△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且∠A＝90°，AB＝5，AC＝12，则阴影部分的周长是 ．
7．（2022秋•滨湖区校级期中）如图，AC是矩形ABCD的对角线，⊙O是△ABC的内切圆，现将矩形ABCD按如图所示的方式折叠，使点D与点O重合，折痕为FG，点F、G分别在AD、BC上，连结OG、DG，若OG⊥DG，且⊙O的半径长为1，则BC﹣AB的值 ，CD+DF的值 ．
8．（2022秋•盐都区月考）【阅读理解】三角形中线长公式：三角形两边平方的和，等于所夹中线和第三边一半的平方和的两倍如图（1），在△ABC中，点D是BC中点，则有：AB2+AC2＝2（AD2+BD2）．
【问题解决】请利用上面的结论，解决下面问题：如图（2），点C、D是以AB为直径的⊙O上两点，点P是OB的中点，点E是CD的中点，且∠CPD＝90，若AB＝8，当△EPB面积最大时，则CD的长为 ．
三．解答题（共4小题）
9．（2022秋•盐都区期中）如图，在Rt△ACB中，∠C＝90°，点D在AC上，∠CBD＝∠A，过A、D两点的圆的圆心O在AB上．
（1）判断BD所在直线与⊙O的位置关系，并证明你的结论；
（2）若AE＝8，∠A＝30°，求图中由BD、BE、围成阴影部分面积．
10．（2022秋•海陵区校级期中）如图，在Rt△ABC中，∠ACB＝90°，分别以AB，BC，CA为直径作半圆围成两月牙形，过点C作DF∥AB分别交三个半圆于点D，E，F．
（1）连结AF、BD，求证四边形AFDB为矩形．
（2）若CF，CD，求阴影部分的面积．
11．（2022秋•镇江期中）如图，在▱ABCD中，AB＝4，BC＝8，∠ABC＝60°．点P是射线BC上一动点，作△PAB的外接圆⊙O．
（1）当DC与△PAB的外接圆⊙O相切时，求⊙O的半径；
（2）直接写出⊙O与▱ABCD的边的公共点的个数及对应的BP长的取值范围．
12．（2022秋•兴化市期中）如图1，已知AB为⊙O的直径，点E在⊙O上，给出下列信息：
①EF是⊙O的切线②AC⊥EF③AE平分∠BAC．
（1）请在上述3条信息中选择其中两条作为条件，剩余的一条信息作为结论，组成一个正确的命题，你选择的条件是 ，结论是 （只要填写序号），并说明理由；
（2）如图2，在（1）的条件下，AC交⊙O于D，若AD＝2，EC，求AE的值．