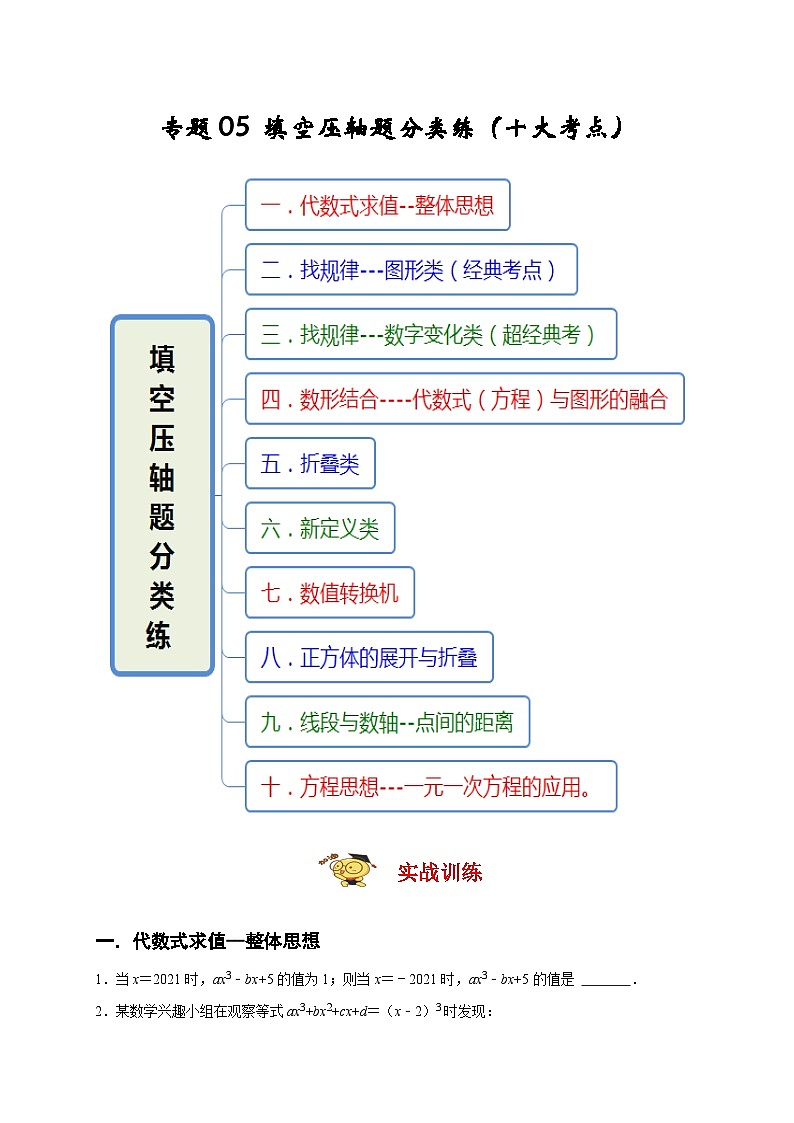
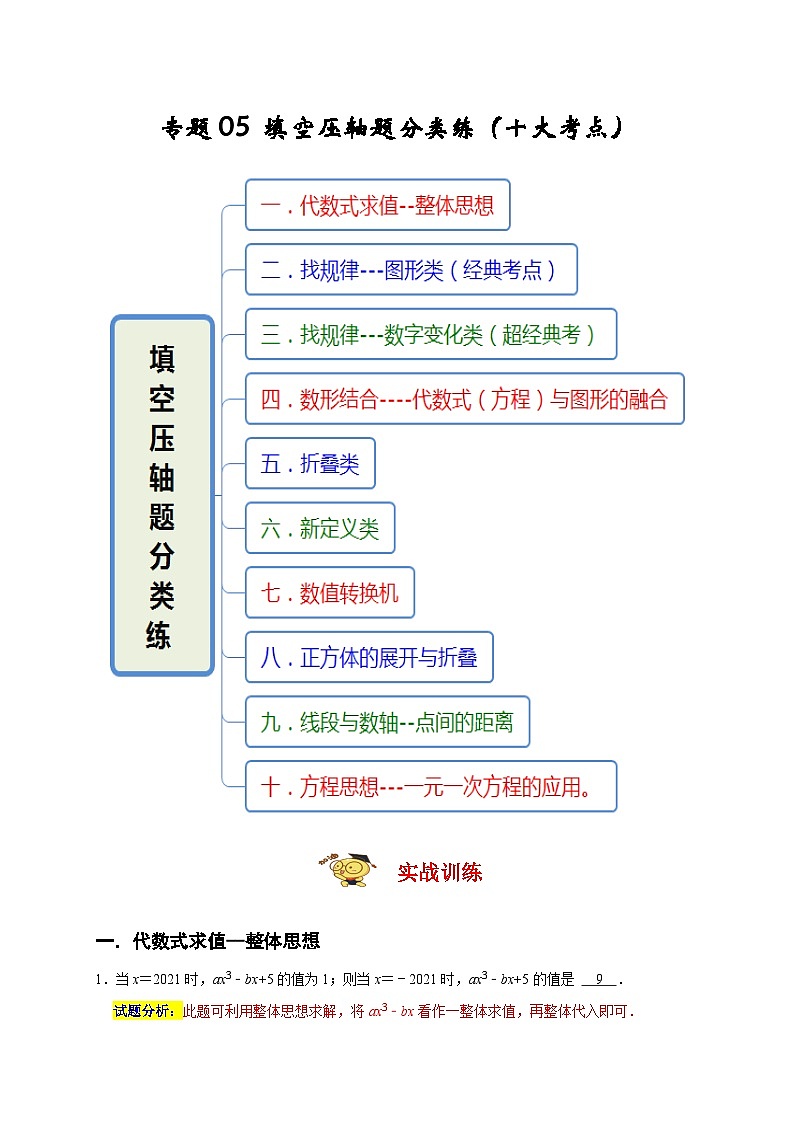
人教版数学七年级上册期末培优训练专题05 填空压轴题分类练（2份，原卷版+解析版）

这是一份人教版数学七年级上册期末培优训练专题05 填空压轴题分类练（2份，原卷版+解析版），文件包含人教版数学七年级上册期末培优训练专题05填空压轴题分类练原卷版doc、人教版数学七年级上册期末培优训练专题05填空压轴题分类练解析版doc等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。
实战训练
一．代数式求值--整体思想
1．当x＝2021时，ax3﹣bx+5的值为1；则当x＝﹣2021时，ax3﹣bx+5的值是 9 ．
试题分析：此题可利用整体思想求解，将ax3﹣bx看作一整体求值，再整体代入即可．
答案详解：解：当x＝2021时，ax3﹣bx+5＝1，ax3﹣bx＝﹣4，
由于ax3﹣bx中x均为奇数幂，
故当x＝2021时的代数式ax3﹣bx的值与当x＝﹣2021时的代数式ax3﹣bx的值互为相反数，
即当x＝﹣2021时，ax3﹣bx＝4，
所以当x＝﹣2021时，ax3﹣bx+5＝4+5＝9，
所以答案是：9．
2．某数学兴趣小组在观察等式ax3+bx2+cx+d＝（x﹣2）3时发现：
当x＝1时，a+b+c+d＝（1﹣2）3＝﹣1．
请你解决下列问题：
（1）﹣a+b﹣c+d＝ （﹣1﹣2）3＝﹣27 ；
（2）8a+4b+2c＝ 8 ．
试题分析：（1）利用x＝﹣1，代入等式ax3+bx2+cx+d＝（x﹣2）3即可得到结果；
（2）利用x＝0代入等式，即可得到d的值，再把x＝2代入等式，把d的值代入等式，即可求出值．
答案详解：解：（1）把x＝﹣1代入等式，得
﹣a+b﹣c+d＝（﹣1﹣2）3，
∴﹣a+b﹣c+d＝（﹣3）3＝﹣27，
所以答案是：﹣27；
（2）把x＝0代入等式，得
d＝（0﹣2）3＝（﹣2）3＝﹣8，
把x＝2代入等式，得
8a+4b+2c+d＝（2﹣2）3，
∴8a+4b+2c+d＝0，
∴8a+4b+2c﹣8＝0，
∴8a+4b+2c＝8，
所以答案是：8．
二．找规律---图形类（经典考点）
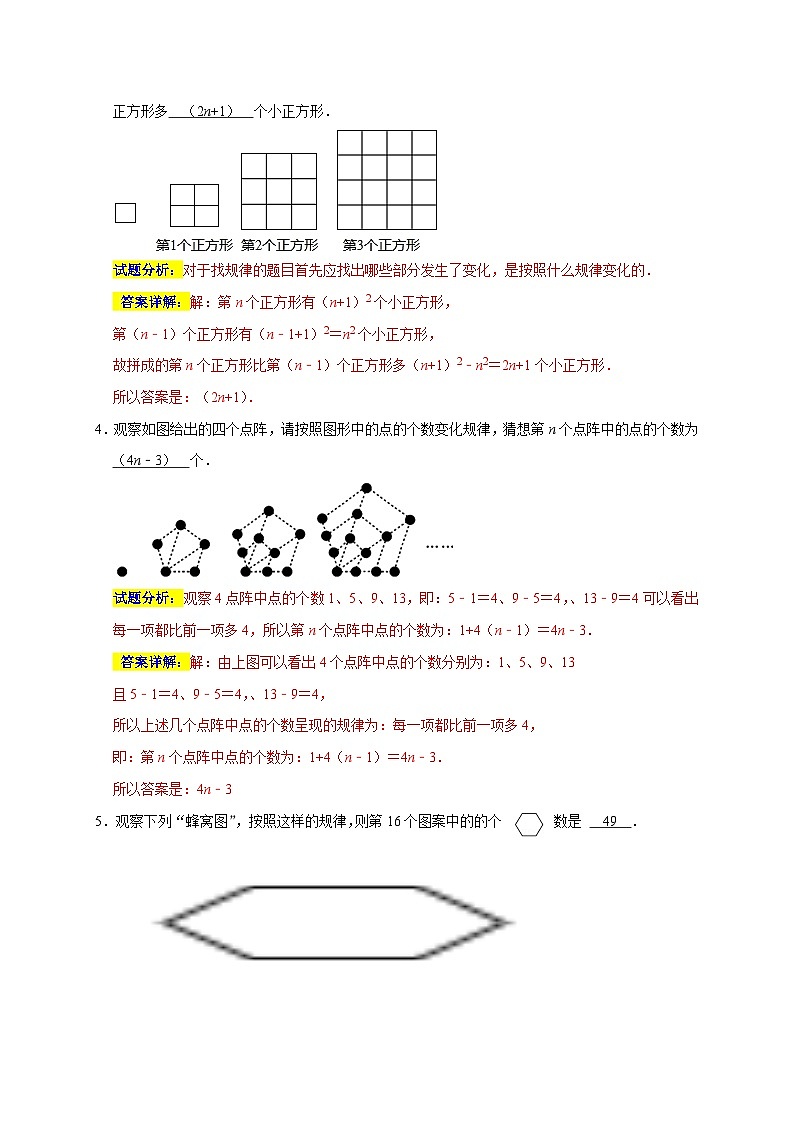
3．如图所示，用大小相等的小正方形拼大正方形，拼第一个正方形需要4个小正方形，拼第二个正方形需要9个小正方形…拼一拼，想一想，按照这样的方法拼成的第n个正方形比第（n﹣1）个正方形多 （2n+1） 个小正方形．
试题分析：对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．
答案详解：解：第n个正方形有（n+1）2个小正方形，
第（n﹣1）个正方形有（n﹣1+1）2＝n2个小正方形，
故拼成的第n个正方形比第（n﹣1）个正方形多（n+1）2﹣n2＝2n+1个小正方形．
所以答案是：（2n+1）．
4．观察如图给出的四个点阵，请按照图形中的点的个数变化规律，猜想第n个点阵中的点的个数为 （4n﹣3） 个．
试题分析：观察4点阵中点的个数1、5、9、13，即：5﹣1＝4、9﹣5＝4，、13﹣9＝4可以看出每一项都比前一项多4，所以第n个点阵中点的个数为：1+4（n﹣1）＝4n﹣3．
答案详解：解：由上图可以看出4个点阵中点的个数分别为：1、5、9、13
且5﹣1＝4、9﹣5＝4，、13﹣9＝4，
所以上述几个点阵中点的个数呈现的规律为：每一项都比前一项多4，
即：第n个点阵中点的个数为：1+4（n﹣1）＝4n﹣3．
所以答案是：4n﹣3
5．观察下列“蜂窝图”，按照这样的规律，则第16个图案中的的个数是 49 ．
试题分析：从数字找规律，进行计算即可解答．
答案详解：解：由题意得：
第一个图案中的“”的个数是：4＝4+3×0，
第二个图案中的“”的个数是：7＝4+3×1，
第三个图案中的“”的个数是：10＝4+3×2，
..．
∴第16个图案中的“”的个数是：4+3×15＝49，
所以答案是：49．
三．找规律---数字变化类（超经典考）
6．有若干个数，第一个数记为a1，第二个数记为a2，…，第n个数记为an．若a1，从第二个数起，每个数都等于“1与它前面那个数的差的倒数”，a2021＝ ．
试题分析：先利用倒数的定义计算出a2，a3，a4，则可判断循环排列，由于2021÷3＝673……2，所以a2021＝a2．
答案详解：解：由题意得：
a1，
a2，
a33，
a4，
…
则该数据为，，3的循环排列，
∵2021÷3＝673……2，
∴a2021＝a2．
所以答案是：．
7．观察下列等式找出规律①13＝12；②13+23＝32；③13+23+33＝62；④13+23+33+43＝102；…则（﹣11）3+（﹣12）3+（﹣13）3+…+（﹣20）3的值是 ﹣41075 ．
试题分析：根据题目中式子的特点，通过变形可以求得（﹣11）3+（﹣12）3+（﹣13）3+…+（﹣20）3的结果．
答案详解：解：∵（﹣11）3+（﹣12）3+（﹣13）3+…+（﹣20）3
＝﹣（113+123+133+…+203）
＝﹣[（13+23+33+…+203）﹣（13+23+33+…+103）]
＝﹣（2102﹣552）
＝﹣（210+55）×（210﹣55）
＝﹣265×155
＝﹣41075，
所以答案是：﹣41075．
8．观察下面三行数：
1，﹣4，9，﹣16，25，﹣36，…；
﹣1，﹣6，7，﹣18，23，﹣38，…；
﹣2，8，﹣18，32，﹣50，72，…；
那么取每行数的第10个数，则这三个数的和为 ﹣2 ．
试题分析：根据题目中的数字，得出这三行中每一行的第10个数字，再计算和即可．
答案详解：解：由题目中的数字可得，
第1行的数字是平方数，奇数个是正，偶数个是负，故第10个数字是﹣100，
第2行数字比第1行的数字小2，故第10个数字是﹣102，
第3行的数字是第1行数字的﹣2倍，故第10个数字是200．
所以这三个数的和为﹣100﹣102+200＝﹣2，
所以答案是：﹣2．
9．观察下列三行数，并完成填空：
①﹣2，4，﹣8，16，﹣32，64，…
②1，﹣2，4，﹣8，16，﹣32，…
③0，﹣3，3，﹣9，15，﹣33，…
第①行数按一定规律排列，第2022个数是 22022 ；若取每行数的第2022个数，计算这三个数的和为 ﹣1 ．
试题分析：由题可得规律：①第n个数是（﹣2）n，②第n个数是（﹣2）n﹣1，③第n个数是（﹣2）n﹣1﹣1，再求第2022个数即可．
答案详解：解：由①﹣2，4，﹣8，16，﹣32，64，…
可得第n个数是（﹣2）n，
∴第2022个数是22022，
由②1，﹣2，4，﹣8，16，﹣32，…
可得第n个数是（﹣2）n﹣1，
∴第2022个数是﹣22021，
由③0，﹣3，3，﹣9，15，﹣33，…
可得③的每一个数是②的对应数﹣1，
∴第n个数是（﹣2）n﹣1﹣1，
∴第2022个数是﹣22021﹣1，
∴22022﹣22021﹣22021﹣1＝﹣1，
所以答案是：22022，﹣1．
10．已知表格内每一横行中从第二个数起的数都比它左边相邻的数大m，各竖列中从第二个数起的数都比它上面相邻的数大n，则mn+xy+uv＝ 295 ．
试题分析：根据横行12与18的关系求出m＝3，再由数列中12与27的关系求出n＝5，再依次求出x、y、u、v，即可求解．
答案详解：解：∵每一横行中从第二个数起的数都比它左边相邻的数大m，
∴18﹣12＝2m，
∴m＝3，
∵各竖列中从第二个数起的数都比它上面相邻的数大n，
∴27﹣12＝3n，
∴n＝5，
∴y＝12+3﹣5＝10，
x＝27﹣6﹣5＝16，
u＝27+3＝30，
v＝12﹣3﹣5＝4，
∴mn+xy+uv＝3×5+10×16+30×4＝295，
所以答案是：295．
11．观察下面的一列单项式：x，﹣2x2，4x3，﹣8x4，…根据你发现的规律，第n个单项式为 （﹣2）n﹣1xn ．
试题分析：要看各单项式的系数和次数与该项的序号之间的变化规律．本题中，奇数项符号为正，数字变化规律是2n﹣1，字母变化规律是xn．
答案详解：解：由题意可知第n个单项式是（﹣2）n﹣1xn．
所以答案是：（﹣2）n﹣1xn．
四．数形结合----代数式（方程）与图形的融合
12．如图，两个多边形的面积分别为13和22，两个阴影部分的面积分别为a，b（a＜b），则b﹣a的值为 9 ．
试题分析：直接根据题意表示出图形总面积进而得出答案．
答案详解：解：设空白部分面积为x，则a+x＝13，b+x＝22，
由题意可得：b+x﹣（a+x）＝b﹣a＝22﹣13＝9．
所以答案是：9．
13．如图，把形如图①所示的形状大小完全相同的小长方形卡片六张，不重叠的摆放在如图②所示的长为8cm，宽为7cm的长方形内，若其未被卡片覆盖的部分是长方形A和长方形B，则长方形A和B的周长和是 32 ．
试题分析：设小长方形的长与宽分别为a、b，根据题意列出算式即可求出答案．
答案详解：解：设小长方形的长与宽分别为a、b，
∴长方形A的长与宽为：a、8﹣3b，
长方形B的长与宽为：8﹣a，3b，
所以长方形A与B的周长之和为：2[a+（8﹣3b）+（8﹣a）+3b]
＝2×16
＝32，
所以答案是：32．
14．如图，由3个相同的长方形A和1个正方形B组成的图形，其中长方形A的长是宽的2倍，则正方形B的周长为 84 ．
试题分析：设长方形A的宽为为x，长为2x，根据正方形的边长可得出关于x的一元一次方程，解之即可得出x的值，再利用正方形的周长公式即可求解．
答案详解：解：设长方形A的宽为为x，长为2x，
根据题意得：x+2x+7.5＝2x+16.5﹣x，
解得：x＝4.5，
∴（x+2x+7.5）×4＝21×4＝84．
所以答案是：84．
五．折叠类
15．如图，将一段标有0～60均匀刻度的绳子铺平后折叠（绳子无弹性），使绳子自身的一部分重叠，然后在重叠部分某处剪断，将绳子分为A，B，C三段．若这三段的长度的比为3：2：1，则折痕对应的刻度是 20 ．
试题分析：设折痕对应的刻度为x，根据折叠的性质和A，B，C三段的长度的比为3：2：1，列出方程求解即可．
答案详解：解：设折痕对应的刻度为x，
由A，B，C三段长度的比为3：2：1，可得三段长度分别是30、20、10，
依题意得：x10＝20，
所以答案是：20．
16．如图1，在长方形ABCD中，点E在AD上，并且∠BEA＝64°，分别以BE，CE为折痕进行折叠并压平，如图2，若图2中∠A'ED'＝18°，则∠DEC的度数为 35° ．
试题分析：利用折叠的性质可得∠AEA′＝2∠BEA＝128°，从而可得∠AED′＝110°，然后利用平角定义可得∠DED′＝70°，再利用折叠的性质进行计算即可解答．
答案详解：解：由折叠得：
∠AEA′＝2∠BEA＝128°，
∵∠A'ED'＝18°，
∴∠AED′＝∠AEA′﹣∠A′ED′＝110°，
∴∠DED′＝180°﹣∠AED′＝70°，
由折叠得：
∠DEC＝∠D′EC∠DED′＝35°，
所以答案是：35°．
17．将一张纸如图所示折叠后压平，点F在线段BC上，EF、GF为两条折痕，若∠1＝57°，∠2＝20°，∠3的度数 23° ．
试题分析：根据折叠，∠1＝∠EFB′，∠3＝∠GFC′，再根据平角意义得∠1+∠EFB′+∠2+∠3+∠GFC′＝180°，由已知求出答案．
答案详解：解：由折叠得，∠1＝∠EFB′，∠3＝∠GFC′，
∵∠1+∠EFB′+∠2+∠3+∠GFC′＝180°，
∵∠1＝57°，∠2＝20°，
∴∠3＝（180°﹣57°×2﹣20°）÷2＝23°，
所以答案是：23°．
六．新定义类
18．[x]表示不超过数x的最大整数，当x＝5.2时，[x]表示的整数为 5 ；若x+2[x]+3[x]+4[x]+…+100[x]＝10100，则x＝ 2 ．
试题分析：要解此方程，必须先去掉[]，根据[x]是整数，2[x]，3[x]，n[x]都是整数，所以x必是整数，即可求解．
答案详解：解：[x]表示不超过数x的最大整数，当x＝5.2时，[x]表示的整数为5；
由于10100是整数，[x]是整数，2[x]，3[x]，…，100[x]都是整数，所以x必是整数．
所以原方程化为x+2x+3x+4x+…+100x＝10100，
合并同类项得（1+2+3+…+100）x＝10100，
适于x＝10100，
所以x＝2．
所以答案是：5，2．
19．如图，射线OC在∠AOB的内部，图中共有3个角：∠AOB，∠AOC和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的“巧分线“．若∠AOB＝60°，且射线OC是∠AOB的“巧分线“，则∠AOC的度数为 20°或30°或40° ．
试题分析：分三种情况：①∠BOC＝2∠AOC；②∠AOB＝2∠AOC；③∠AOC＝2∠BOC；分别求解即可．
答案详解：解：若∠AOB＝60°，且射线OC是∠AOB的“巧分线”，则由“巧分线”的定义可知有三种情况符合题意：
①∠BOC＝2∠AOC，此时∠AOC＝20°；
②∠AOB＝2∠AOC，此时∠AOC＝30°；
③∠AOC＝2∠BOC，此时∠AOC＝40°；
所以答案是：20°或30°或40°．
20．直线l上的三个点A、B、C，若满足BCAB，则称点C是点A关于点B的“半距点”．如图1，BCAB，此时点C就是点A关于点B的一个“半距点”．如图2若M、N、P三个点在同一条直线m上，且点P是点M关于点N的“半距点”，MN＝6cm．则MP＝ 3或9 cm．
试题分析：根据点P是点M关于点N的“半距点”，可得PNMN，分两种情况画图求解．
答案详解：解：（1）如图所示：
∵点P是点M关于点N的“半距点”，
∴PNMN，
①∵MN＝6cm．P1NMN＝3cm，
∴MP1＝MN﹣P1N＝3cm；
②∵MN＝6cm．P2NMN＝3cm，
∴MP2＝MN+P2N＝9cm；
∴MP＝3cm或9cm；
所以答案是：3或9．
21．我们定义：若两个角差的绝对值等于60°，则称这两个角互为“正角”，其中一个角是另一个角的“正角”．如：∠1＝110°，∠2＝50°，|∠1﹣∠2|＝60°，则∠1和∠2互为“正角”．如图，已知∠AOB＝120°，射线OC平分∠AOB，∠EOF在∠AOB的内部，若∠EOF＝60°，则图中互为“正角”的共有 7 对．
试题分析：根据“正角”的定义解答即可．
答案详解：解：∵∠AOB＝120°，射线OC平分∠AOB，
∴∠AOC＝∠BOC，
∴∠AOB﹣∠AOC＝60°，∠AOB﹣∠BOC＝60°，
又∵∠EOF＝60°，
∴∠AOB﹣∠EOF＝60°，
∵∠EOF＝∠AOC＝60°，
∴∠AOF﹣∠AOE＝60°，∠AOF﹣∠COF＝60°，
∠BOE﹣∠EOC＝60°，∠BOE﹣∠BOF＝60°，
∴图中互为“正角”的共有∠AOB与∠AOC，∠AOB与∠BOC，∠AOB与∠EOF，∠AOF与∠AOE，∠AOF与∠COF，∠BOE与∠EOC，∠BOE与∠BOF共7对．
所以答案是：7
七．数值转换机
22．规定计算机按如图所示程序工作，如果输出的数是125，那么输入的自然数是 11或30 ．
试题分析：根据程序图列式计算．
答案详解：解：当输出的数为125时，
125÷5+5＝25+5＝30，
30÷5+5＝6+5＝11，
11不能被5整除，
∴输入的自然数是11或30，
所以答案是：11或30．
八．正方体的展开与折叠
23．将下图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，应剪去 1或2或6 ．（填序号）
试题分析：利用正方体及其表面展开图的特点解题．
答案详解：解：根据有“田”字格的展开图都不是正方体的表面展开图可知．故应剪去1或2或6．
所以答案是：1或2或6．
24．如图所示的是一个正方体的平面展开图．若将平面展开图折叠成正方体后，相对面上的两个数字之和均为﹣5，则x+y+z的值为 0 ．
试题分析：根据正方体表面展开图的特征，可得出相对的面，求出x、y、z，代入计算即可．
答案详解：解：根据正方体展开图的“相间、Z端是对面”的特征可知，
“﹣2”与“y”相对，
“﹣10”与“z”相对，
“x”与“﹣3”相对，
又∵相对面上的两个数字之和均为﹣5，
∴x＝﹣2，y＝﹣3，z＝5，
∴x+y+z＝﹣2﹣3+5＝0，
所以答案是：0．
九．线段与数轴--点间的距离
25．如图，有一种电子游戏，电子屏幕上有一条直线，在直线上有A，B，C，D四点．点P沿直线l从右向左移动，当出现点P与A，B，C，D四点中的至少两个点距离相等时，就会发出警报，则直线l上会发出警报的点P最多有 6 个．
试题分析：点P与A，B，C，D四点中的至少两个点距离相等时，也就是点P恰好是其中一条线段中点．而图中共有线段六条，所以出现报警次数最多6次．
答案详解：解：由题意知，当P点经过任意一条线段中点的时候会发出警报，
∵图中共有线段DC、DB、DA、CB、CA、BA，
∴发出警报的可能最多有6个．
所以答案是：6．
26．如图，点C、D为线段AB上两点，AC+BD＝3，AD+BCAB，则CD等于 ．
试题分析：由题可得AC+BD+2CD（AC+BD+CD），再将AC+BD＝3代入即可求解．
答案详解：解：∵AD+BC＝AC+BD+2CD，
又∵AD+BCAB，
∴AC+BD+2CD（AC+BD+CD），
∵AC+BD＝3，
∴3+2CD（3+CD），
∴CD，
所以答案是：．
27．如图，点A，B，C，D，E，F都在同一直线上，点B是线段AD的中点，点E是线段CF的中点，有下列结论：①AE（AC+AF），②BEAF，③BE（AF﹣CD），④BC（AC﹣CD）．其中正确的结论是 ①③④ （只填相应的序号）．
试题分析：AE＝AC+CE＝AB+BC+CE，BE＝BD+DE＝BD+CE﹣CD＝CD，BC＝AD﹣AB﹣CD＝AB﹣CD（AC﹣CD）﹣CD（AC﹣CD）．
答案详解：解：AE＝AC+CE＝AB+BC+CE＝AB+BE，故①正确；
BE＝BD+DE＝BD+CE﹣CDAD+1/2CF﹣CD（AD+CF）﹣CD（AF+CD）﹣CD（AF﹣CD），故②错误，③正确；
BC＝AD﹣AB﹣CD＝AB﹣CD（AC+CD）﹣CD（AC﹣CD），④正确．
所以答案是：①③④
28．已知：如图，E，F为线段MN上的两点，点E为MF的中点，若MN＝25，图中所有线段的和为80（不重复计），则线段NF的长是 15 ．
试题分析：先找出图中所有的线段，然后根据题目的已知条件即可解答．
答案详解：解：由题意得：
ME+MF+MN+EF+EN+FN＝80，
∴（ME+EF+FN）+MN+MF+EN＝80，
∴MN+MN+MF+FN+EF＝80，
∴3MN+EF＝80，
∵MN＝25，
∴EF＝5，
∵点E为MF的中点，
∴MF＝2EF＝10，
∴NF＝MN﹣MF＝15，
所以答案是：15．
29．如图，点Q在线段AP上，其中PQ＝10，
第一次分别取线段AP和AQ的中点P1，Q1，得到线段P1Q1，则线段P1Q1＝ 5 ；
再分别取线段AP1和AQ1的中点P2，Q2，得到线段P2Q2；
第三次分别取线段AP2和AQ2的中点P3，Q3，得到线段P3Q3；连续这样操作2021次，则每次的两个中点所形成的所有线段之和P1Q1+P2Q2+P3Q3+…+P2021Q2021＝ 10 ．
试题分析：根据线段中点的定义可得P1Q1PQ，P2Q2P1Q1，P3Q3P2Q2，根据规律可得答案．
答案详解：解：∵线段AP和AQ的中点是P1，Q1，
∴P1Q1＝AP1﹣AQ1APAQPQ＝5，
∵线段AP1和AQ1的中点P2，Q2，
∴P2Q2＝AP2﹣AQ2AP1AQ1P1Q1PQPQ，
∵线段AP2和AQ2的中点P3，Q3，
∴P3Q3＝AP3﹣AQ3AP2AQ2P2Q2PQPQ，
…，
∴P1Q1+P2Q2+P3Q3+…+P2021Q2021
PQPQPQPQ
＝（）PQ
＝（1）PQ
＝10．
所以答案是：5，10．
30．线段AB＝6，C为线段AB的中点，点D在直线AB上，若BD＝3AC，则CD＝ 12或6 ．
试题分析：分两种情况，点D在点B的右侧，点D在点B的左侧．
答案详解：解：分两种情况：
当点D在点B的右侧时，如图：
∵点C是线段AB的中点，AB＝6，
∴CBAB＝3，
∵BD＝3AC＝9，
∴CD＝CB+BD＝3+9＝12，
当点D在点B的左侧时，如图：
∵点C是线段AB的中点，AB＝6，
∴CBAB＝3，
∵BD＝3AB＝9，
∴CD＝BD﹣CB＝9﹣3＝6，
∴线段CD的长为12或6，
所以答案是：12或6．
31．一副三角板AOB与COD如图1摆放，且∠A＝∠C＝90°，∠AOB＝60°，∠COD＝45°，ON平分∠COB，OM平分∠AOD．当三角板COD绕O点顺时针旋转（从图1到图2）．设图1、图2中的∠NOM的度数分别为α，β，α+β＝ 105 度．
试题分析：根据角平分线的意义，以及角的和与差，分别表示出∠MON，然后利用两个图形分别计算α、β即可．
答案详解：解：如图1，∵ON平分∠COB，OM平分∠AOD．
∴∠NOB＝∠CON∠BOC（45°+∠BOD），
∠MOD＝∠MOA∠AOD（60°+∠BOD），
∴∠MON＝α＝∠NOB+∠MOD﹣∠BOD（45°+60°），
如图2，∵ON平分∠COB，OM平分∠AOD．
∴∠NOB＝∠CON∠BOC（45°﹣∠BOD），
∠MOD＝∠MOA∠AOD（60°﹣∠BOD），
∴∠MON＝β＝∠NOB+∠MOD+∠BOD（45°+60°），
∴α+β＝45°+60°＝105°，
所以答案是：105．
十．方程思想---一元一次方程的应用。
32．某小组同学在小型运动会中表现出色，作为奖励他们组得到了一盒乒乓球，如果每位同学分3个乒乓球，那么还剩余8个；如果每位同学分5个乒乓球，那么还差4个．则该小组共有 6 名同学．
试题分析：设该小组共有x名同学，根据乒乓球总数不变列方程，即可解得答案．
答案详解：解：设该小组共有x名同学，根据题意得：
3x+8＝5x﹣4，
解得：x＝6，
答：该小组共有6名同学；
所以答案是：6．
33．春节将近，各服装店清仓大甩卖．一商店某一时间以每件120元的价格卖出两件衣服，其中一件盈利50%，另一件亏损20%，卖这两件衣服的利润为 10 元．
试题分析：已知售价，需算出这两件衣服的进价，让总售价减去总进价就算出了总的盈亏
答案详解：解：设盈利50%的那件衣服的进价是x元，
根据进价与得润的和等于售价列得方程：x+0.5x＝120，
解得：x＝80，
类似地，设另一件亏损衣服的进价为y元，它的商品利润是﹣20%y元，
列方程y+（﹣20%y）＝120，
解得：y＝150．
那么这两件衣服的进价是x+y＝230元，而两件衣服的售价为240元．
则240﹣230＝10（元）．
故卖这两件衣服的利润为10元．
所以答案是：10．
34．如图所示的是2022年2月份的月历，2022年2月1日恰逢春节，也是农历壬寅虎年的开始．月历中，“U型”、“十字型”两个阴影图形分别覆盖其中五个数字（“U型”、“十字型”两个阴影图形可以重叠覆盖，也可以上下左右移动），设“U型”覆盖的五个数字之和为S1，“十字型”覆盖的五个数字之和为S2．若S1+S2＝186，则S2﹣S1的最大值为 ﹣16 ．
试题分析：设“U”型阴影覆盖的最小数字为a，则其它的数字分别是（a+2）、（a+7）、（a+8）、（a+9），设“十字型”阴影覆盖的最小数字为ab，则其它数字分别为（b﹣1）、（b+1）、（b﹣7）、（b+7），然后根据S1+S2＝186，列出方程求得a与b的等量关系，代入S2﹣S1中分析最值．
答案详解：解：设“U”型阴影覆盖的最小数字为a，则其它的数字分别是（a+2）、（a+7）、（a+8）、（a+9），
∴S1＝a+（a+2）+（a+7）+（a+8）+（a+9）＝5a+26，
设“十字型”阴影覆盖的中间数字为b，则其它数字分别为（b﹣1）、（b+1）、（b﹣7）、（b+7），
∴S2＝b+（b﹣1）+（b+1）+（b﹣7）+（b+7）＝5b，
∵S1+S2＝186，
∴5a+26+5b＝186，
整理可得：a+b＝32，即b＝32﹣a，
∴S2﹣S1＝5b﹣（5a+26）
＝5b﹣5a﹣26
＝5（32﹣a）﹣5a﹣26
＝160﹣5a﹣5a﹣26
＝﹣10a+134，
∵﹣10＜0，
∴S2﹣S1的值随着a的增大而减小，
又∵b＝32﹣a，
∴在符合题意的情况下，当b＝18时，a有最小值为14，
∴此时S2﹣S1有最大值为﹣10×14+134＝﹣140+134＝﹣6，
所以答案是：﹣6．
35．一只猴子摘了一堆桃子，第一天它吃了这堆桃子的，第二天它吃了余下桃子的，第三天它吃了余下桃子的，第四天它吃了余下桃子的，第五天它吃了余下桃子的，第六天它吃了余下桃子的，这时还剩7只桃子，那么第一天和第二天猴子所吃桃子的总数是 14只 ．
试题分析：设这堆桃子共有x只，则前六天每天吃了x只桃子，还剩下x只桃子，由还剩7只桃子，可得出x＝7，再将其代入xx中即可求出第一天和第二天猴子所吃桃子的总数．
答案详解：解：设这堆桃子共有x只，则第一天吃了x只桃子，第二天吃了（xx）x只桃子，第三天吃了（xxx）x只桃子，第四天吃了（xxxx）x只桃子，第五天吃了（1xxxx）x只桃子，第六天吃了（xxxxxx）x只桃子，还剩下xxxxxxxx只桃子，
依题意得：x＝7，
∴第一天和第二天猴子所吃桃子的总数是xx＝7+7＝14．
所以答案是：14只．
36．已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若P，Q两点同时出发，问运动时间为 1或9 秒时，点P和点Q间的距离为8个单位长度．
试题分析：设点P运动x秒时，点P与点Q间的距离为8个单位长度，然后分两种情况：①当Q在P点左边时，②当P在Q的左边时分别列出方程，再解即可．
答案详解：解：设点P运动x秒时，点P与点Q间的距离为8个单位长度，由题意得：
①当Q在P点左边时，4x+10﹣6x＝8，
解得：x＝1，
②当P在Q的左边时，6x﹣（4x+10）＝8，
解得：x＝9，
所以答案是：1或9．
37．寒假到来，某书店开展学生优惠购买名著活动，凡一次性购买不超过100元的，一律九折优惠；超过100元的，其中100元按九折优惠，超过100元的部分按八折优惠．小青第一次去购买时付款36元，第二次又去购买时享受到了八折优惠．他查看了所买名著的定价，发现两次共节省了17元，则小青第二次购买时实际付款 102 元．
试题分析：先求出第一次购书时的实际定价，再根据第二次购书节省的钱数列出方程，再求解即可．
答案详解：解：第一次购书付款36元，享受了九折优惠，实际定价为36÷0.9＝40元，省去了4元钱．
依题意，第二次节省了：17﹣4＝13元．
设第二次所购书的定价为x元．（x﹣100）×0.8+100×0.9＝x﹣13，
解得x＝115．
故第二次购书实际付款为：115﹣13＝102元．
所以答案是：102．
38．今年3.15期间，惠东商场为感谢新老顾客，决定对某产品实行优惠政策：购买该产品，另外赠送礼品一份．经过与该产品的供应商协调，供应商同意将该产品供货价格降低5%，同时免费为顾客提供礼品；而该产品的商场零售价保持不变．这样一来，该产品的单位利润率由原来的x%提高到（x+6）%，则x的值是 14 ．
试题分析：设原来的进价为a元，则现在的进价为（1﹣0.05）a元，则原来的售价为a（1+x%），现在的售价为0.95a[1+（x+6）%]，根据两次的售价相等建立方程求出其解得．
答案详解：解：原来的进价为a元，则现在的进价为（1﹣0.05）a元，由题意，得
a（1+x%）＝0.95a[1+（x+6）%]，
解得：x＝14
所以答案是：14