清单01 直线的倾斜角与斜率、直线方程问题（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019）

这是一份清单01 直线的倾斜角与斜率、直线方程问题（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019），文件包含清单01直线的倾斜角与斜率直线方程问题清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019原卷版docx、01直线的倾斜角与斜率直线方程问题清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019解析版docx等2份学案配套教学资源，其中学案共28页， 欢迎下载使用。

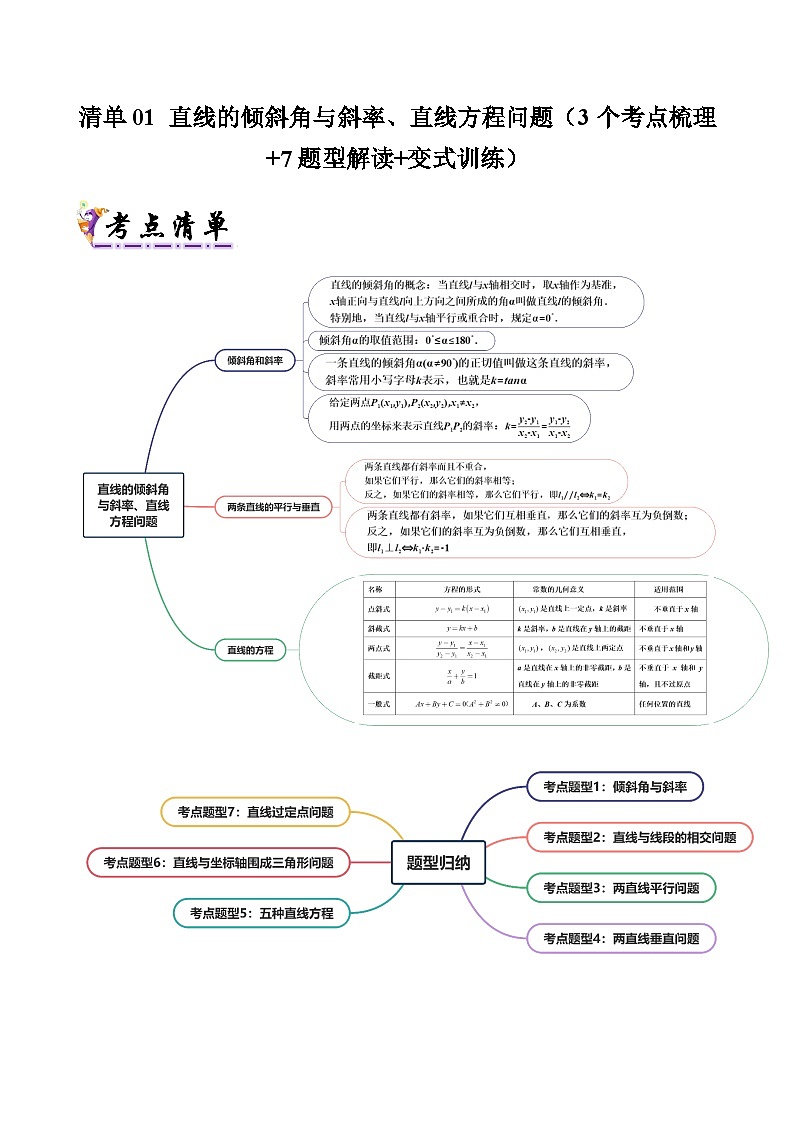
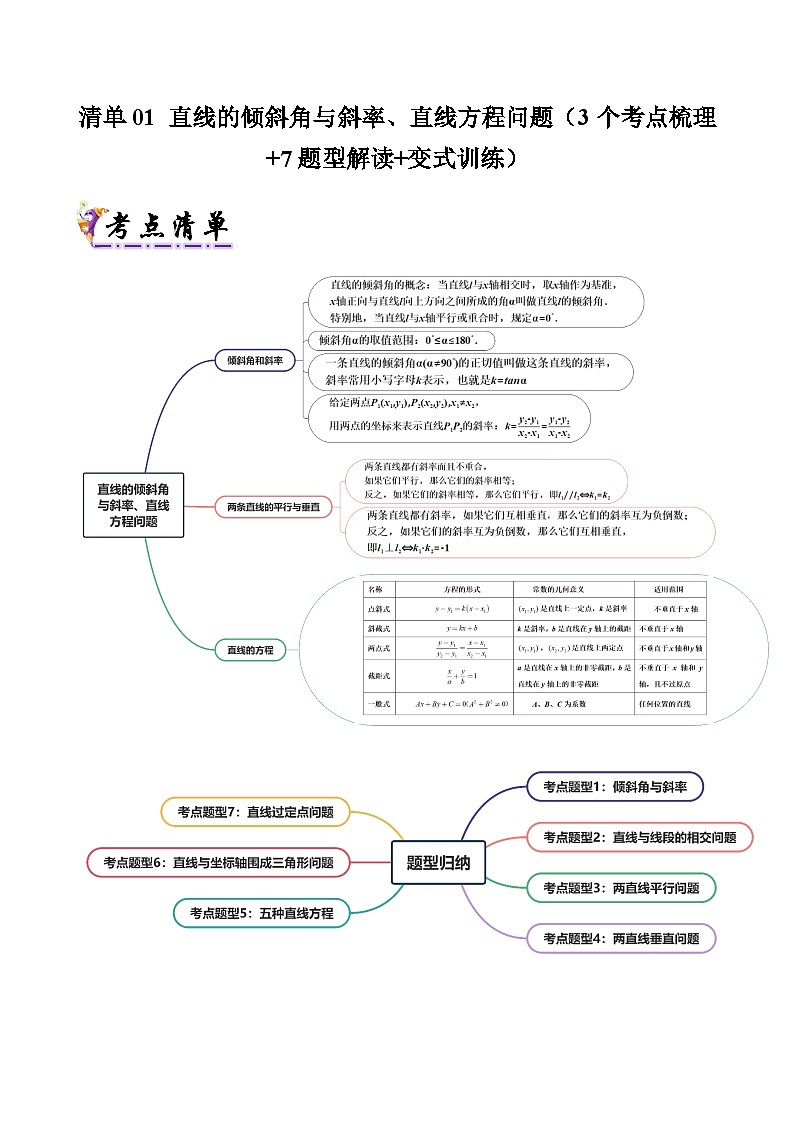
【清单01】倾斜角和斜率
（1）直线的倾斜角的概念：当直线l与x轴相交时，取x轴作为基准，x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角．特别地，当直线l与x轴平行或重合时，规定．
（2）倾斜角α的取值范围：．当直线l与x轴垂直时，．
（3）直线的斜率：
一条直线的倾斜角的正切值叫做这条直线的斜率，斜率常用小写字母k表示，也就是
①当直线l与x轴平行或重合时，，；
②当直线l与x轴垂直时，，k不存在．
由此可知，一条直线l的倾斜角α一定存在，但是斜率k不一定存在．
（4）直线的斜率公式：
给定两点，用两点的坐标来表示直线的斜率：
【清单02】两条直线的平行与垂直
（1）两条直线都有斜率而且不重合，如果它们平行，那么它们的斜率相等；反之，如果它们的斜率相等，那么它们平行，即
注意：上面的等价是在两条直线不重合且斜率存在的前提下才成立的，缺少这个前提，结论并不成立．即如果，那么一定有
（2）两条直线都有斜率，如果它们互相垂直，那么它们的斜率互为负倒数；反之，如果它们的斜率互为负倒数，那么它们互相垂直，即
【清单03】直线的方程
直线方程的五种形式的比较如下表：
考点题型1：倾斜角与斜率
【典例1-1】（23-24高二下·湖南邵阳·期末）已知直线的倾斜角为，则直线的斜率为（ ）
A．B．C．1D．
【答案】C
【解析】由直线的倾斜角为，
则直线的斜率，
故选：C.
【典例1-2】（23-24高二下·河南驻马店·期末）直线的倾斜角是（ ）
A．0B．C．πD．不存在
【答案】B
【解析】直线垂直于x轴，所以直线的倾斜角是.
故选：B
【变式1-1】（23-24高二下·江苏盐城·期末）过两点、的直线的倾斜角为，则的值为（ ）
A．或B．C．D．
【答案】D
【解析】因为过两点、的直线的倾斜角为，
所以，即，解得.
故选：D
【变式1-2】（23-24高二下·上海嘉定·期末）直线与直线的夹角为（ ）
A．B．C．D．
【答案】B
【解析】设两直线的倾斜角分别为，由，则，
由，则，即，
则两直线夹角为.
故选：B.
【变式1-3】（23-24高二上·四川成都·期末）直线的一个方向向量为（ ）
A．B．−3,2C．2,3D．
【答案】B
【解析】由得，，
所以直线的一个方向向量为，
而，所以也是直线的一个方向向量.
故选：B.
考点题型2：直线与线段的相交问题
【典例2-1】（23-24高二上·山东威海·期末）已知点，，若直线与线段有公共点，则（ ）
A．B．
C．D．
【答案】B
【解析】
若与线段有公共点，分析必过，且，，则.
故选：B
【典例2-2】（21-22高二上·云南曲靖·期末）经过点作直线，若直线与连接两点的线段总有公共点，则直线的斜率的取值范围为（ ）
A．B．
C．D．
【答案】D
【解析】，，画出图像，如图所示：
根据图像知：.
故选：D.
【变式2-1】（23-24高二上·山西吕梁·阶段练习）经过点作直线l，若直线l与连接，两点的线段总有公共点，设l的倾斜角为，l的斜率为 k，则（ ）
A．B．
C．D．
【答案】A
【解析】设直线的倾斜角为，
,
所以，即，
由题意知：，
解得：或．
倾斜角的取值范围是
故BCD错误，A正确，
故选：A
【变式2-2】（22-23高二上·广东深圳·期末）已知、，若直线经过点，且与线段有交点，则的斜率的取值范围为（ ）
A．B．
C．D．
【答案】D
【解析】过点作，垂足为点，如图所示：
设直线交线段于点，设直线的斜率为，且，，
当点在从点运动到点（不包括点）时，直线的倾斜角逐渐增大，
此时；
当点在从点运动到点时，直线的倾斜角逐渐增大，此时.
综上所述，直线的斜率的取值范围是.
故选：D.
【变式2-3】（22-23高二上·贵州贵阳·阶段练习）已知直线，若直线与连接，两点的线段总有公共点，则直线的倾斜角范围为（ ）
A．B．
C．D．
【答案】D
【解析】直线的方程可化为，
联立方程组，可得，所以直线过定点，
由题意得，直线的斜率一定存在，
设直线的斜率为，直线的倾斜角为，则，
因为直线的斜率为，直线的斜率为，
因为直线经过点，且与线段总有公共点，
所以，即，
因为，所以或，
又直线的斜率，所以，
故直线的倾斜角的取值范围是．
故选：D．
考点题型3：两直线平行问题
【典例3-1】（22-23高二下·河北石家庄·期末）已知直线与直线 平行，则直线l 的斜率为（ ）
A．B．C．D．
【答案】D
【解析】由题可知直线与直线斜率相同，将一般式化为斜截式，所以斜率为23.
故选：D
【典例3-2】（23-24高二下·江苏南京·期末）“”是“两条直线平行”的（ ）
A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件
【答案】A
【解析】因为两条直线平行，
所以直线斜率相等或斜率不存在，
当两直线斜率不存在时，即，两直线为x=1，成立；
当两直线斜率存在时，即，解得，两直线为成立，
综上或.
所以“”是“两条直线平行”的充分不必要条件.
故选：A.
【变式3-1】（23-24高二上·福建泉州·期末）记平面直角坐标系内的直线、与x轴正半轴方向所成的角的正切值分别为、，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．既不充分也不必要条件D．充要条件
【答案】A
【解析】由题意可知：已经存在，
若∥，则，即充分性成立；
若，则可能重合，即必要性均不成立；
综上所述：“”是“”的充分不必要条件.
故选：A．
【变式3-2】（23-24高二上·陕西西安·期末）已知直线与直线平行，则实数的所有取值之和为（ ）
A．-2B．C．1D．2
【答案】B
【解析】因为直线与直线平行，
所以，解得或1，经检验均满足题意，
所以实数的所有取值之和为.
故选：B
【变式3-3】（23-24高二上·河南驻马店·期末）已知两条不重合的直线和．若，则实数的值为（ ）
A．B．C．1D．或1
【答案】B
【解析】因为，故，故或，
当时，的方程均为，它们重合，故舍去；
当时，，，它们平行，
故选：B.
考点题型4：两直线垂直问题
【典例4-1】（23-24高二上·安徽蚌埠·期末）直线的方向向量是，则下列选项中的直线与直线垂直的是（ ）
A．B．
C．D．
【答案】A
【解析】因为直线的方向向量是，所以直线斜率，
所以与直线垂直的直线的斜率为.
对于选项A:由，可得斜率为，故选项A正确；
对于选项B:由，可得斜率为，故选项B错误；
对于选项C:由，可得斜率为，故选项C错误；
对于选项D:由，可得斜率为，故选项D错误.
故选：A.
【典例4-2】（23-24高二上·山东潍坊·期末）已知两直线的斜率分别为，且是方程的两根，则与的位置关系为（ ）
A．平行B．相交且垂直C．重合D．相交且不垂直
【答案】B
【解析】由题意，因此两直线垂直．平面上的两直线垂直时当然相交．
故选：B．
【变式4-1】（22-23高二下·山东济南·期末）直线与直线的位置关系是（ ）
A．垂直B．相交且不垂直C．平行D．平行或重合
【答案】A
【解析】当时，直线，直线，此时两直线垂直，
当时，直线的斜率，直线的斜率，
因为，则两直线垂直，
综上两直线位置关系是垂直，
故选：A.
【变式4-2】（23-24高二上·福建福州·期末）若直线与直线垂直，则实数a的取值是（ ）
A．或B．
C．D．
【答案】A
【解析】直线与直线垂直，
则有，解得或，
故选：A．
【变式4-3】（23-24高二上·江苏南京·期末）在平面直角坐标系中，若直线与直线互相垂直，则实数的值是（ ）
A．-1B．C．D．3
【答案】C
【解析】直线与直线互相垂直，
则，解得.
故选：C
考点题型5：五种直线方程
【典例5-1】（23-24高二上·新疆克孜勒苏·期末）（1）求经过点，倾斜角为的直线的一般式方程．
（2）的三个顶点是，求边BC上的中线所在的直线方程．
【解析】（1）由倾斜角为可得直线斜率为，由于经过点，
代入点斜式方程得，即：；
（2）设边的中点为，根据中点坐标公式得，
从而可得中线所在直线方程为，即：．
【典例5-2】（23-24高二上·湖南长沙·期末）已知直线与直线的交点为．
(1)求过点且与直线垂直的直线方程；
(2)求过点且与直线平行的直线方程．
【解析】（1）联立方程与，解得，，故，
而的斜率为，故所求直线斜率为，
则所求直线方程为，化简得.
（2）易知的斜率为，故所求直线斜率为，
则所求直线方程为，化简得.
【变式5-1】（23-24高二上·上海嘉定·期末）已知方程（）．
(1)求该方程表示直线的条件；
(2)当为何实数时，方程表示的直线斜率不存在？求出此时的直线方程；
(3)直线是否过定点，若存在直线过定点，求出此定点，若不存在，说明理由．
【解析】（1）当，的系数不同时为时，方程表示一条直线，
令，解得或；
令，解得或，
所以，的系数同时为零时，
故若方程表示一条直线，则，
即实数的取值范围为；
（2）当的系数不为，的系数为时斜率不存在，
由（1）知当时，且，方程表示的直线的斜率不存在，
此时直线方程为；
（3）不过定点，证明如下：
证明：当的系数为，的系数不为时斜率为，
由（1）知当时，且，方程表示的直线的斜率为，
此时直线方程为，
由（2）知，直线的斜率不存在时直线方程为，
由得交点为，
若直线过定点，则定点为，
将代入方程，
得，
整理得，解得或，
只有当或时，直线过，
直线不过定点.
【变式5-2】（23-24高二上·北京石景山·期末）菱形的顶点的坐标分别为边所在直线过点.
(1)求边所在直线的方程；
(2)求对角线所在直线的方程.
【解析】（1）由菱形的性质可知，则.
所以边所在直线的方程为，即；
边所在直线的方程为，即.
（2）线段的中点为，
由菱形的几何性质可知，且为的中点，则，
所以对角线所在直线的方程为，即.
【变式5-3】（23-24高二上·辽宁沈阳·期中）已知的三个顶点分别是，求：
(1)边所在直线的一般式方程；
(2)边的垂直平分线所在直线的斜截式方程．
【解析】（1）由直线方程的两点式，得，
所以直线的一般式方程为．
（2）边的中点坐标为．
因为边所在直线的斜率为，
所以直线的斜率为．
所以直线的方程为，即．
【变式5-4】（22-23高二上·河南平顶山·阶段练习）求符合下列条件的直线的方程：
(1)过点，且斜率为；
(2)过点，；
(3)过点且在两坐标轴上的截距相等．
【解析】（1）∵所求直线过点，且斜率为，∴，即；
（2）∵所求直线过，，∴，
∴，即；
（3）当直线过原点时，设直线方程为，
∵直线过点，∴，直线方程为，即；
当直线不过原点时，设直线方程为，
将点代入上式，得，解得，
故直线的方程为，综上，直线方程为或．
考点题型6：直线与坐标轴围成三角形问题
【典例6-1】（23-24高二上·贵州·阶段练习）已知直线的方程为.
(1)证明：不论为何值，直线过定点.
(2)过（1）中点，且与直线垂直的直线与两坐标轴的正半轴所围成的三角形的面积最小时，求直线的方程.
【解析】（1）证明：直线的方程，
可整理为.
由，解得，
所以直线过定点.
（2）由（1）知，直线过定点，
设过点且与直线垂直的直线方程为，
令，则.
令，则.
所以，
所以，
当且仅当，即时，等号成立，
所以直线的斜率为，
所以直线的方程为，即.
【典例6-2】（23-24高二上·安徽黄山·期中）已知直线．
(1)若直线l不经过第二象限，求k的取值范围．
(2)若直线l与x轴、y轴正半轴分别交于A、B两点，当△AOB的面积为时（O为坐标原点），求此时相应的直线l的方程．
【解析】（1）由题意可知直线，
易知直线过定点，
当直线过原点时，可得，
当时，直线不经过第二象限．
（2）由题意可知
∵直线与轴、轴正半轴的交点分别是，
，
当时，由得：
，
即：，
或，
即：直线的方程为或.
【变式6-1】（22-23高二上·天津武清·阶段练习）已知直线经过点．
(1)若直线与直线垂直，求的直线方程；
(2)设直线的斜率，且l与两坐标轴的交点分别为A、B，当的面积最小时，求的直线方程．
【解析】（1）解:若直线与直线垂直,则可设直线的方程为
又直线经过点，所以，得
则的直线方程为：
（2）设直线的斜率，则直线
直线与两坐标轴交点分别为,、0,，
则面积为，
又
当且仅当时，等号成立，
故面积最小值为4，此时直线方程为：.
【变式6-2】已知直线l：kx－y＋1＋2k＝0（k∈R）．
（1）证明：直线l过定点；
（2）若直线l不经过第四象限，求k的取值范围；
（3）若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，求S的最小值及此时直线l的方程．
【解析】（1）证明：
直线l的方程可化为y＝k（x＋2）＋1，故无论k取何值，直线l总过定点（－2，1）．
（2）直线l的方程为y＝kx＋2k＋1，则直线l在y轴上的截距为2k＋1，要使直线l不经过第四象限，则解得k≥0，故k的取值范围是．
（3）依题意，直线l在x轴上的截距为，在y轴上的截距为1＋2k，
∴A，B（0，1＋2k）．
又且1＋2k＞0，
∴k＞0．
故S＝|OA||OB|＝××（1＋2k）＝≥×（4＋）＝4，
当且仅当4k＝，即k＝时，取等号．
故S的最小值为4，此时直线l的方程为x－2y＋4＝0．
【变式6-3】（23-24高二下·上海静安·阶段练习）设直线l的方程为．
(1)若直线l在两坐标轴上的截距相等，求直线l的方程；
(2)若，直线l与x、y轴分别交于M、N两点，求△OMN面积取最值时，直线l的方程．
【解析】（1）由，令，令，
由直线方程在两坐标轴上的截距相等，则，解得或，
故直线方程：或
（2）由（1）可知，，
当且仅当，即取等号.
即直线方程：.
【变式6-4】（23-24高二上·安徽·期末）已知直线过点．
(1)若直线在轴上的截距、在轴上的截距的满足，求直线的方程；
(2)若直线与两坐标轴的正半轴分别交于，两点，为坐标原点，当的面积最小时，求直线的方程．
【解析】（1）根据题意：直线在轴上的截距是在轴上的截距的3倍，
当直线不过原点时，设直线为，
将代入可得，
所以直线的方程为；
当直线过原点时，直线的斜率为，
所以直线的方程为即．
综上，直线的方程为或；
（2）设直线的方程为，
所以，，
所以，
当且仅当时，，（舍），
所以直线的方程为即．
考点题型7：直线过定点问题
【典例7-1】（23-24高二上·福建泉州·期末）直线恒过定点 .
【答案】
【解析】由直线，可化为，
联立方程组，解得，所以直线恒过定点．
故答案为：．
【典例7-2】（23-24高二上·上海·期末）已知直线：恒过定点，则定点坐标是 .
【答案】0,2
【解析】令，即，可得，
所以直线：恒过定点.
故答案为：.
【变式7-1】（23-24高二上·陕西安康·期末）直线恒过定点 ．
【答案】
【解析】将直线化为，
令，解得，
故直线的恒过点为.
故答案为：
【变式7-2】（23-24高二下·上海宝山·期末）若无论实数取何值，直线都经过一个定点，则该定点坐标为 .
【答案】
【解析】令，解得，故经过的定点坐标为.
故答案为：
【变式7-3】（23-24高二上·江苏南通·期末）直线经过的定点坐标为 .
【答案】
【解析】已知直线方程化为，
由得，所以直线过定点．
故答案为：．
名称
方程的形式
常数的几何意义
适用范围
点斜式
是直线上一定点，k是斜率
不垂直于x轴
斜截式
k是斜率，b是直线在y轴上的截距
不垂直于x轴
两点式
，是直线上两定点
不垂直于x轴和y轴
截距式
a是直线在x轴上的非零截距，b是直线在y轴上的非零截距
不垂直于x轴和y轴，且不过原点
一般式
A、B、C为系数
任何位置的直线