清单02 直线的交点、距离公式与对称、最值问题（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019）

这是一份清单02 直线的交点、距离公式与对称、最值问题（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019），文件包含清单02直线的交点距离公式与对称最值问题清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019原卷版docx、02直线的交点距离公式与对称最值问题清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019解析版docx等2份学案配套教学资源，其中学案共33页， 欢迎下载使用。

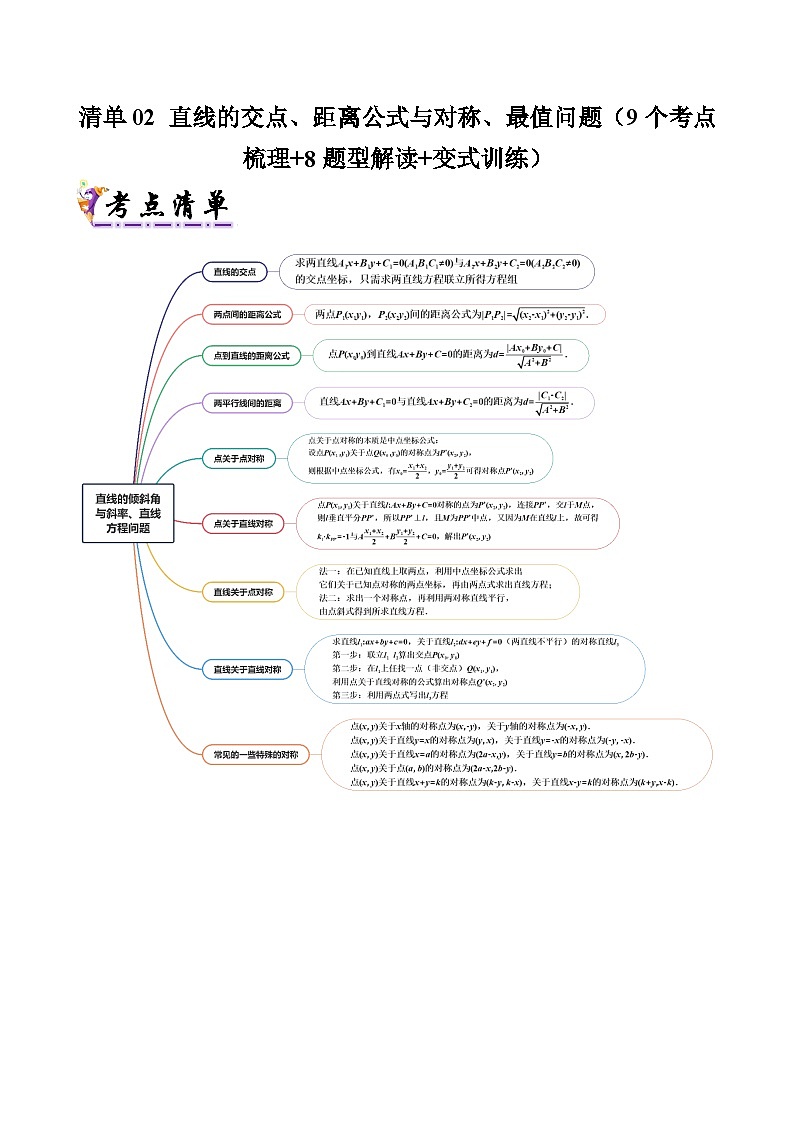
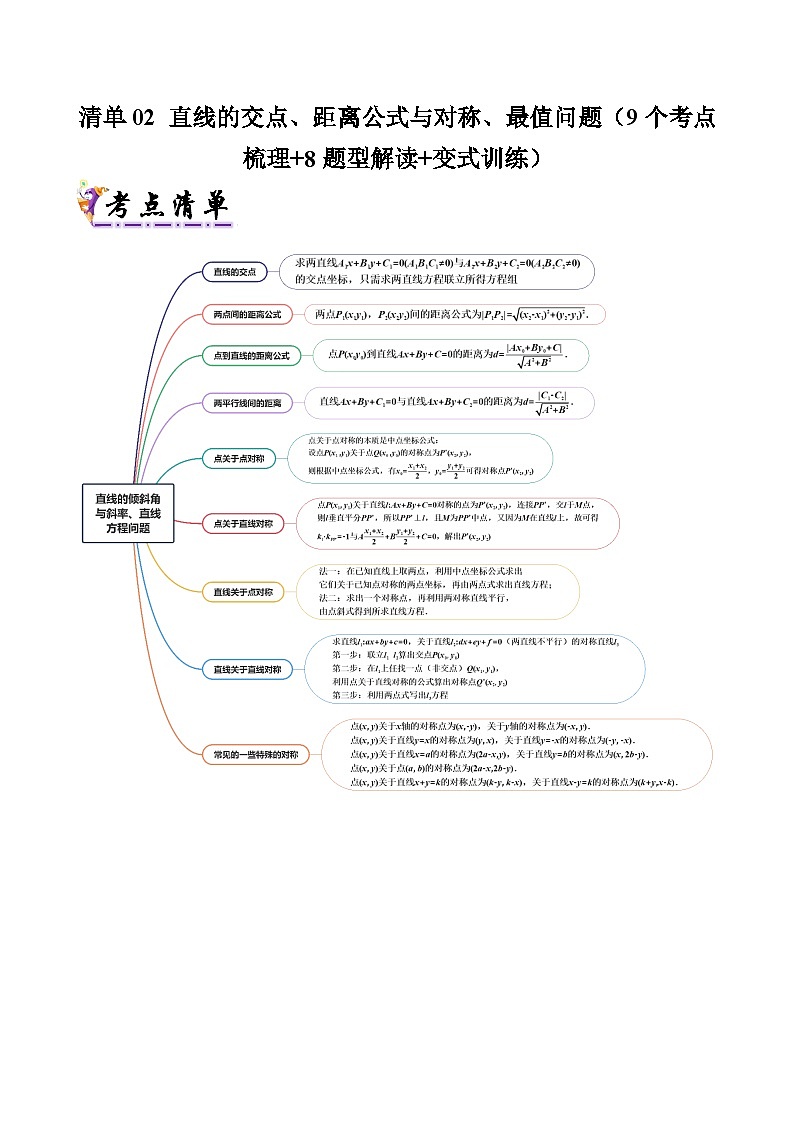
【清单01】直线的交点
求两直线与的交点坐标，只需求两直线方程联立所得方程组的解即可．若有，则方程组有无穷多个解，此时两直线重合；若有，则方程组无解，此时两直线平行；若有，则方程组有唯一解，此时两直线相交，此解即两直线交点的坐标．
【清单02】两点间的距离公式
两点，间的距离公式为．
【清单03】点到直线的距离公式
点到直线的距离为．
【清单04】两平行线间的距离
直线与直线的距离为．
【清单05】点关于点对称
点关于点对称的本质是中点坐标公式：设点关于点的对称点为，则根据中点坐标公式，有
可得对称点的坐标为
【清单06】点关于直线对称
点关于直线对称的点为，连接，交于点，则垂直平分，所以，且为中点，又因为在直线上，故可得，解出即可．
【清单07】直线关于点对称
法一：在已知直线上取两点，利用中点坐标公式求出它们关于已知点对称的两点坐标，再由两点式求出直线方程；
法二：求出一个对称点，再利用两对称直线平行，由点斜式得到所求直线方程．
【清单08】直线关于直线对称
求直线，关于直线（两直线不平行）的对称直线
第一步：联立算出交点
第二步：在上任找一点（非交点），利用点关于直线对称的秒杀公式算出对称点
第三步：利用两点式写出方程
【清单09】常见的一些特殊的对称
点关于轴的对称点为 ，关于轴的对称点为．
点关于直线的对称点为，关于直线的对称点为．
点关于直线的对称点为，关于直线的对称点为．
点关于点的对称点为 ．
点关于直线的对称点为 ，关于直线的对称点为 ．
考点题型1：两直线的交点问题
【典例1-1】若直线：与直线相交，且交点在第一象限，则直线的倾斜角的取值范围是（ ）
A．B．
C．D．
【典例1-2】（23-24高二上·四川凉山·期末）经过两条直线和的交点，且垂直于直线的直线方程为（ ）
A．B．
C．D．
【变式1-1】（23-24高二上·湖南·期末）若三条不同的直线，，不能围成一个三角形，则a的取值集合为（ ）
A．B．C．D．
【变式1-2】（23-24高二上·重庆长寿·期末）直线与直线的交点坐标是（ ）
A．B．C．D．
【变式1-3】（23-24高二上·海南海口·期末）过两直线与的交点，并且与第一条直线垂直的直线方程是（ ）
A．B．C．D．
考点题型2：两点的距离
【典例2-1】（23-24高三下·浙江丽水·开学考试）设点A,B在曲线上．若的中点坐标为，则（ ）
A．6B．C．D．
【典例2-2】（23-24高二上·天津·期末）三角形的三个顶点为，D为中点，则的长为（ ）
A．3B．5C．9D．25
【变式2-1】（23-24高二上·新疆喀什·期末）已知点与点之间的距离为5，则实数a的值为 ．
【变式2-2】（23-24高二上·广西南宁·期末）已知函数且过定点，直线过定点，则
【变式2-3】（23-24高二上·四川宜宾·期末）过定点的直线与过定点的直线交于，则
考点题型3：点到直线的距离
【典例3-1】（23-24高二上·河南南阳·期末）点为两条直线和的交点，则点到直线：的距离最大为（ ）
A．B．C．D．5
【典例3-2】（23-24高二上·广西北海·期末）已知点到直线的距离相等，则（ ）
A．－1或0B．C．－1D．2
【变式3-1】（23-24高二上·新疆·期末）点到直线的距离为（ ）
A．B．2C．D．1
【变式3-2】（23-24高二上·四川绵阳·期末）已知，两点到直线：的距离相等，则（ ）
A．B．6C．或4D．4或6
【变式3-3】（23-24高二上·浙江绍兴·期末）原点到直线的距离的最大值为（ ）
A．B．C．D．
考点题型4：两平行直线的距离
【典例4-1】（23-24高二上·河北石家庄·阶段练习）两平行直线和之间的距离为（ ）
A．B．2C．D．3
【典例4-2】（23-24高二上·湖北孝感·期末）两条平行直线与间的距离为（ ）
A．B．1C．D．
【变式4-1】（23-24高二上·福建三明·期末）两条平行线，间的距离等于（ ）
A．B．C．D．
【变式4-2】（23-24高二上·福建福州·期末）已知直线与直线间的距离为2，则（ ）
A．或4B．4C．或6D．或16
【变式4-3】（23-24高二上·广东深圳·期末）若直线与直线间的距离为，则（ ）
A．17B．C．14D．7
考点题型5：点线对称
【典例5-1】（23-24高二上·山东泰安·期末）点关于直线的对称点的坐标为（ ）
A．B．C．D．
【典例5-2】（23-24高二上·湖北荆门·期末）一条光线从射出与x轴相交于点，经x轴反射，交y轴于R，则光线从P到R所走的路程为 ．
【变式5-1】（23-24高二上·上海·期末）已知点与点关于直线l对称，则直线l的方程为 ．
【变式5-2】（21-22高二上·湖北随州·期中）光线沿直线入射到直线后反射，则反射光线所在直线的方程为 ．
【变式5-3】（22-23高二上·江苏盐城·期末）已知的一条内角平分线CD的方程为，两个顶点为，，则顶点C的坐标 ．
考点题型6：线点对称
【典例6-1】（23-24高二上·全国·期末）点在直线上，直线与关于点0,1对称，则一定在直线上的点为（ ）
A．B．C．D．（1，0）
【典例6-2】（21-22高二上·湖北孝感·期末）设直线和直线的交点为.
(1)若直线经过点，且与直线垂直，求直线的方程；
(2)若直线与直线关于点对称，求直线的方程.
【变式6-1】（23-24高二上·江苏常州·期中）已知直线与直线关于点对称，则实数的值为（ ）
A．2B．6C．D．
【变式6-2】（多选题）（23-24高二上·山西太原·期中）已知直线，则下列说法正确的是（ ）
A．直线与相交于点
B．直线和轴围成的三角形的面积为
C．直线关于原点O对称的直线方程为
D．直线关于直线对称的直线方程为
【变式6-3】（多选题）（23-24高二上·福建厦门·期中）已知直线，则（ ）
A．直线l始终过第二象限
B．时，直线l的倾斜角为
C．时，直线l关于原点对称的直线方程为
D．点到直线l的最大距离为
考点题型7：线线对称
【典例7-1】（23-24高二上·山东青岛·期中）直线关于x轴对称的直线方程为（ ）
A．B．
C．D．
【典例7-2】（2023·上海静安·二模）设直线与关于直线对称，则直线的方程是（ ）
A．B．
C．D．
【变式7-1】（2023高三·全国·专题练习）直线关于直线对称的直线方程为
【变式7-2】（22-23高二上·北京大兴·期末）直线关于y轴对称的直线的方程为 ．
【变式7-3】（21-22高二·全国·课后作业）已知点，直线，直线.
(1)求点A关于直线的对称点B的坐标；
(2)求直线关于直线的对称直线方程.
考点题型8：两线段和与差的最值问题
【典例8-1】（23-24高二上·福建福州·期末）已知点，，H是直线：上的动点，则的最小值为（ ）
A．6B．C．D．
【典例8-2】（23-24高二上·内蒙古锡林郭勒盟·期末）设直线l：，点，，P为l上任意一点，则的最小值为（ ）
A．B．C．D．
【变式8-1】（23-24高二上·浙江杭州·期末）已知点Mx1,y1在直线，点Nx2,y2在直线上，且，的最小值为（ ）
A．B．C．D．5
【变式8-2】（23-24高二上·江苏宿迁·期末）我国著名数学家华罗庚曾经说过：“数形结合百般好，隔离分家万事休.”事实上有很多代数问题可以转化为几何问题加以解决，根据上述观点，当取得最小值时，实数的值为（ ）
A．B．3C．D．4
【变式8-3】（23-24高二上·湖南·期中）17世纪法国数学家费马在给朋友的一封信中曾提出一个关于三角形的有趣问题：在三角形所在平面内，求一点，使它到三角形每个顶点的距离之和最小.现已证明：在中，若三个内角均小于，则当点满足时，点到三角形三个顶点的距离之和最小，点被人们称为费马点.根据以上知识，已知，，，P为内一点，记，则的最小值为（ ）
A．B．C．D．
【变式8-4】（23-24高二上·重庆·期末）的最小值为（ ）
A．B．C．D．
【变式8-5】（23-24高二上·江苏南京·期末）已知点 在直线 上，点，则当 的周长取得最小值时，点 的坐标为 .
【变式8-6】（23-24高二上·上海松江·期末）已知分别在直线与直线上，且，点，，则的最小值为