清单03 圆的方程（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019）

这是一份清单03 圆的方程（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019），文件包含清单03圆的方程清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019原卷版docx、03圆的方程清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019解析版docx等2份学案配套教学资源，其中学案共26页， 欢迎下载使用。

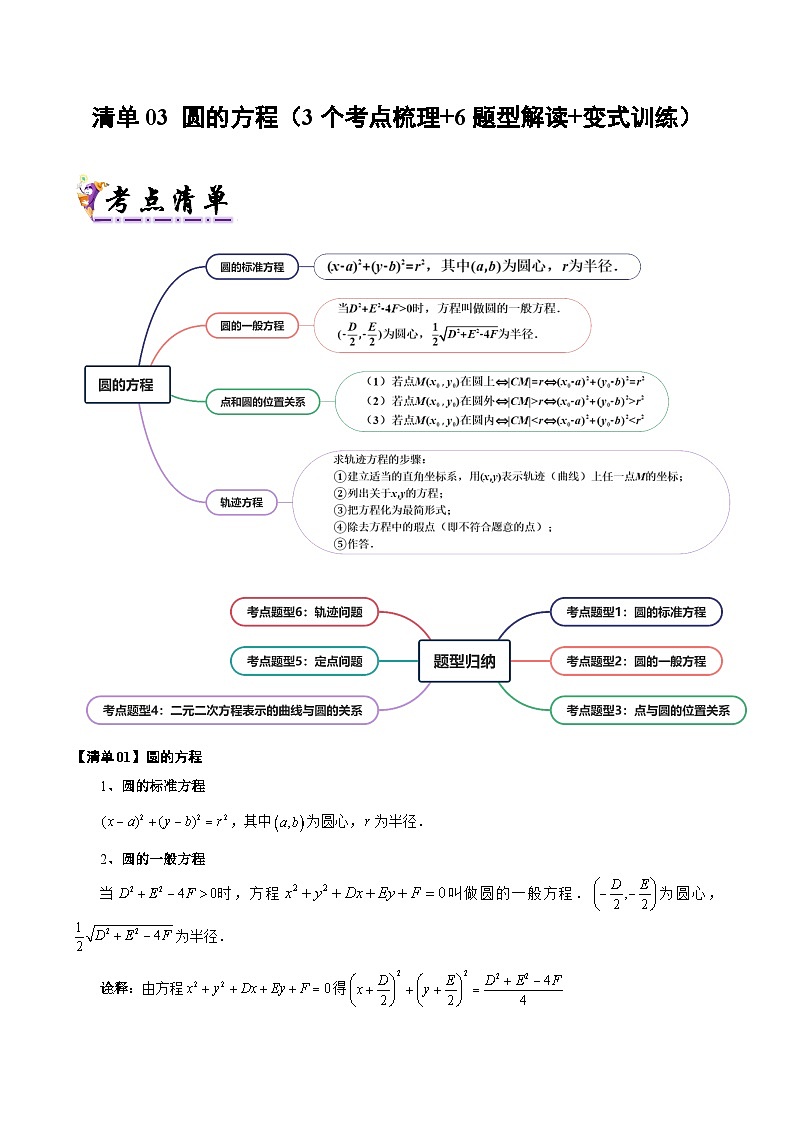
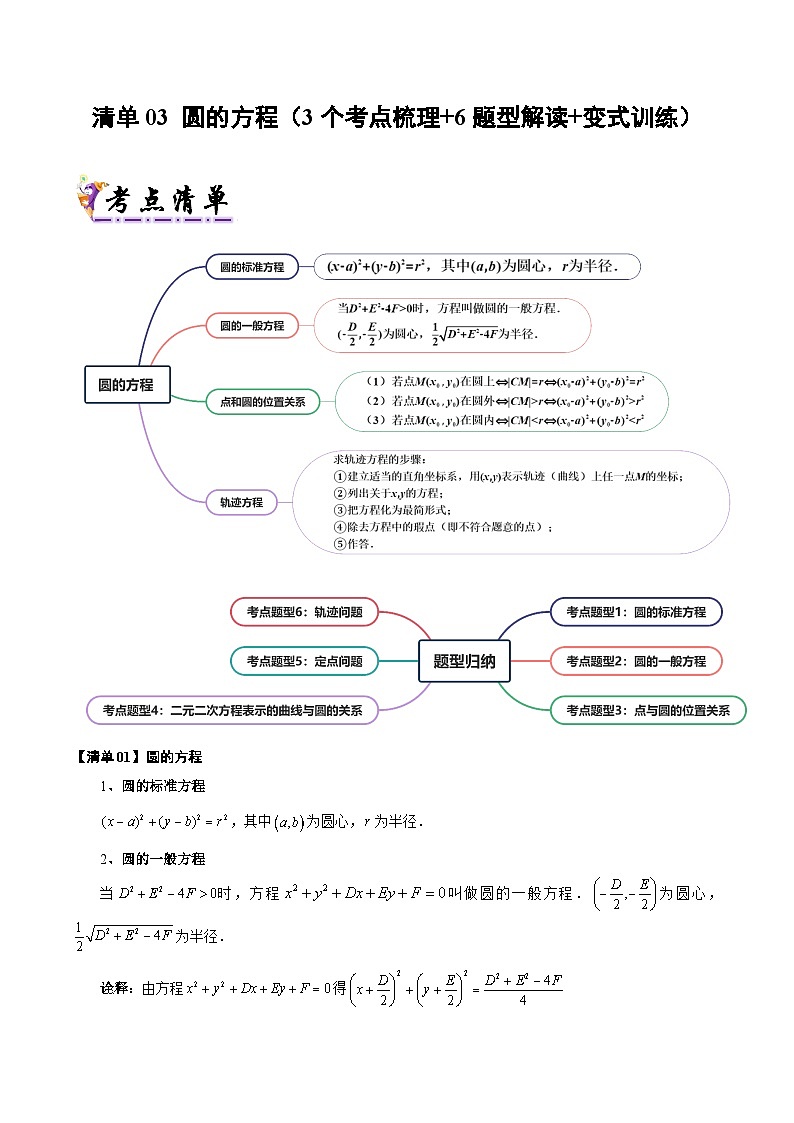
【清单01】圆的方程
1、圆的标准方程
，其中为圆心，为半径．
2、圆的一般方程
当时，方程叫做圆的一般方程．为圆心，为半径．
诠释：由方程得
（1）当时，方程只有实数解．它表示一个点．
（2）当时，方程没有实数解，因而它不表示任何图形．
（3）当时，可以看出方程表示以为圆心，为半径的圆．
3、用待定系数法求圆的方程的步骤
求圆的方程常用“待定系数法”．用“待定系数法”求圆的方程的大致步骤是：
（1）根据题意，选择标准方程或一般方程．
（2）根据已知条件，建立关于或的方程组．
（3）解方程组，求出或的值，并把它们代入所设的方程中去，就得到所求圆的方程．
【清单02】点和圆的位置关系
如果圆的标准方程为，圆心为，半径为，则有
（1）若点在圆上
（2）若点在圆外
（3）若点在圆内
【清单03】轨迹方程
求符合某种条件的动点的轨迹方程，实质上就是利用题设中的几何条件，通过“坐标法”将其转化为关于变量之间的方程．
（1）当动点满足的几何条件易于“坐标化”时，常采用直接法；当动点满足的条件符合某一基本曲线的定义（如圆）时，常采用定义法；当动点随着另一个在已知曲线上的动点运动时，可采用代入法（或称相关点法）．
（2）求轨迹方程时，一要区分“轨迹”与“轨迹方程”；二要注意检验，去掉不合题设条件的点或线等．
（3）求轨迹方程的步骤：
①建立适当的直角坐标系，用表示轨迹（曲线）上任一点的坐标；
②列出关于的方程；
③把方程化为最简形式；
④除去方程中的瑕点（即不符合题意的点）；
⑤作答．
考点题型1：圆的标准方程
【典例1-1】（24-25高二上·江苏盐城·期中）圆，圆与圆关于直线对称，则圆的标准方程为（ ）
A．B．
C．D．
【答案】A
【解析】设，的圆心，半径，
由题意则与关于直线对称，
所以，解得，
所以圆的标准方程为，
故选：A
【典例1-2】（23-24高二上·河北邯郸·期末）已知圆过点，则圆的标准方程是（ ）
A．
B．
C．
D．
【答案】A
【解析】由在圆上，故圆心在直线上，
由在圆上，故圆心在直线上，
即圆心，半径，
故方程为.
故选：A.
【变式1-1】（24-25高二上·浙江台州·期中）已知圆经过，两点，且圆心在直线，则圆的标准方程是（ ）
A．B．
C．D．
【答案】C
【解析】设圆心为，
由题意得，即，
解得，故圆心，
半径为，
故圆的标准方程为.
故选：C
【变式1-2】（24-25高二上·河南濮阳·期中）若圆过，两点，则当圆的半径最小时，圆的标准方程为（ ）
A．B．
C．D．
【答案】D
【解析】依题意，线段的中点，，
圆过，两点，当圆的半径最小时，线段为圆的直径，
所以圆的标准方程为.
故选：D
【变式1-3】（22-23高二下·河南开封·期末）已知圆 与圆关于直线对称，则圆的标准方程为（ ）
A．B．
C．D．
【答案】A
【解析】由题意可得，圆的圆心坐标为，圆和圆的半径均为2，
设圆心关于直线的对称点为，
则，解得，
所以圆的标准方程为.
故选：A
考点题型2：圆的一般方程
【典例2-1】（24-25高二上·河南洛阳·期中）已知，，，则的外接圆方程为（ ）
A．B．
C．D．
【答案】D
【解析】设的外接圆方程为，
因为O0,0，，，
所以，解得，
所以的外接圆方程为.
故选：D.
【典例2-2】（23-24高二上·内蒙古锡林郭勒盟·期末）已知圆C经过点和点，且圆心在y轴上，则圆C的方程为（ ）
A．B．
C．D．
【答案】C
【解析】设圆C的方程为，则圆心，
则有，解之得,
则有圆C的方程为，即
故选：C
【变式2-1】（23-24高二上·浙江·期中）若直线与两坐标轴的交点为，则以为直径的圆的方程为（ ）
A．B．
C．D．
【答案】A
【解析】直线与两坐标轴的交点为，
则，
则以为直径的圆半径为，圆心即为中点坐标为，
所以以为直径的圆的方程为，
化简得：.
故选：A
【变式2-2】（22-23高二上·河南驻马店·期末）以，为直径两端点的圆的方程为（ ）
A．B．
C．D．
【答案】A
【解析】，，
的中点坐标为，
以为直径的圆的圆心为，又，
圆的半径为1，
以为直径的圆的方程为即.
故选：A.
【变式2-3】（22-23高二上·天津和平·期末）三个顶点的坐标分别是，，，则外接圆的方程是（ ）
A．B．
C．D．
【答案】C
【解析】设所求圆方程为,
因为，，三点都在圆上，
所以，解得，
即所求圆方程为：.
故选：C.
考点题型3：点与圆的位置关系
【典例3-1】（24-25高二上·陕西榆林·期中）已知两直线与的交点在圆的内部，则实数的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】圆的圆心为，半径为2，
由解得，
则直线与的交点为，
依题意，，解得，
所以实数k的取值范围是.
故选：B
【典例3-2】（23-24高二上·广东惠州·期中）点与圆的位置关系为（ ）
A．点在圆外B．点在圆内C．点在圆上D．与m的值无关
【答案】A
【解析】，
在圆外，
故选：A.
【变式3-1】（24-25高二上·福建泉州·期中）已知点在圆上，点，则的值可能为（ ）
A．1B．7C．13D．15
【答案】B
【解析】因为，所以点在圆内，
圆心，半径，点到圆心的距离为，
所以的取值范围为，所以的值可能为7，
故选：B.
【变式3-2】（24-25高二上·安徽·期中）若点在圆的外部，则实数a的取值范围是（ ）
A．B．
C．D．
【答案】C
【解析】因为点在圆的外部，
则，解得，
所以实数a的取值范围是.
故选：C.
【变式3-3】（23-24高二上·广西·期末）已知两直线与的交点在圆的内部，则实数k的取值范围是（ ）
A．B．
C．D．
【答案】B
【解析】由，得，则两直线与的交点为，
依题意得，解得.
故选：B.
【变式3-4】（23-24高二上·湖北荆门·期末）已知圆的方程为，若点在圆外，则的取值范围是（ ）
A．B．
C．D．
【答案】D
【解析】由题意得，圆的标准方程为，
故，，
又点在圆外，所以，
，或，
所以m的取值范围为．
故选：D.
考点题型4：二元二次方程表示的曲线与圆的关系
【典例4-1】（23-24高二上·福建厦门·期中）若，则方程表示的圆的个数为（ ）
A．1B．2C．3D．4
【答案】B
【解析】若方程表示圆，
则，
解得，
又，所以或，
即程表示的圆的个数为.
故选：B
【典例4-2】（23-24高二上·广东·期末）已知方程表示一个圆，则实数取值范围是（ ）
A． B．
C．D．
【答案】C
【解析】因为方程表示一个圆，
所以，
即，所以或，
故选：C.
【变式4-1】（23-24高二上·贵州六盘水·期末）已知曲线，则“”是“曲线是圆”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
【解析】因为，所以，
若曲线是圆，所以，所以或，
所以“”是“曲线是圆”的充分不必要条件.
故选：A.
【变式4-2】（23-24高二上·广东江门·期末）方程表示一个圆，则实数的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】，即.
故选：D.
【变式4-3】（23-24高二上·四川成都·期末）若方程表示一个圆，则m可取的值为（ ）
A．0B．1C．2D．3
【答案】D
【解析】由方程分别对进行配方得：，
依题意它表示一个圆，须使，解得：或，在选项中只有D项满足.
故选：D.
考点题型5：定点问题
【典例5-1】（23-24高二上·湖北荆州·期末）圆恒过的定点为（ ）
A． B．
C． D．
【答案】D
【解析】圆的方程化为，
由得或，
故圆恒过定点．
故选：D．
【典例5-2】（21-22高二上·浙江温州·期中）点是直线上任意一点，是坐标原点，则以为直径的圆经过定点（ ）
A．和B．和C．和D．和
【答案】D
【解析】设点，则线段的中点为，
圆的半径为，
所以，以为直径为圆的方程为，
即，即，
由，解得或，
因此，以为直径的圆经过定点坐标为、.
故选：D.
【变式5-1】（24-25高二上·江苏苏州·期中）在平面直角坐标系xOy中，二次函数的图象与坐标轴分别交于点A，B，C，记的外接圆为圆①当时，圆E的一般式方程是 ;②圆E恒过的两个定点是 .
【答案】
【解析】①当时，
二次函数的图象与两坐标轴交于点，，，
的外接圆为圆E，
设所求圆的一般方程为，，
令，得，由题意可得，这与是同一个方程，
故，
令x=0，得，由题意可得，
此方程有一个根为，代入此方程得出，
所以圆E的一般方程为；
②设所求圆的一般方程为，，
令，得，由题意可得，这与是同一个方程，
故，
令x=0，得，由题意可得，此方程有一个根为，
代入此方程得出，所以圆E的一般方程为，
当x=0时，或，
故圆E恒过定点.
故答案为：；
【变式5-2】（23-24高二上·河南信阳·期中）圆恒过的定点是 .
【答案】
【解析】圆方程化为，
由解得故圆恒过点.
故答案为：
【变式5-3】（23-24高二上·江西南昌·阶段练习）已知圆，点，平面内一定点（异于点），对于圆上的任意动点，都有为定值，定点的坐标为 ．
【答案】
【解析】设，且，
，
因为为定值，设，
化简得：，与点位置无关，
所以，
解得：或，
因为异于点，所以定点N为.
故答案为：.
考点题型6：轨迹问题
【典例6-1】（24-25高二上·吉林通化·期中）在中，，，，则点的轨迹方程为 ．
【答案】
【解析】设点，
则，，
则，
化简可得，
故答案为：.
【典例6-2】（23-24高二上·北京·期末）已知点和点，直角以BC为斜边，求直角顶点A的轨迹方程 .
【答案】
【解析】方法一：设点，
，，，，
由题意可知：，
，，
整理得：，
三点不共线，
，，应去除.
直角顶点的轨迹方程为：.
方法二：设BC中点为，则，即A在以D为圆心，
为半径的圆上(不能和B、C重合)，
故A的轨迹方程为.
【变式6-1】（23-24高二上·广东珠海·期末）已知点，，若点P满足，则P的轨迹方程为 ．
【答案】
【解析】设，由，故，
化简得：，故P的轨迹方程为.
故答案为：.
【变式6-2】（23-24高二上·广东佛山·期末）已知点，圆上两动点满足，且四边形是矩形．
(1)当点在第一象限且横坐标为3时，求边所在直线的方程；
(2)求点的轨迹方程．
【解析】（1）设点，由，得，直线的斜率，而，
所以直线的方程为，即.
（2）由于线段是圆的弦，则线段的中垂线必过圆心，
又线段的中垂线是矩形的对称轴，因此该对称轴垂直平分线段，即，
显然不重合，当重合时，点重合，则点的轨迹是以为圆心，2为半径的圆（除点外），
所以点的轨迹方程是.
【变式6-3】（23-24高二上·河南南阳·期末）已知圆的圆心为直线与直线的交点，且圆的半径为.
(1)求圆的标准方程；
(2)若为圆上任意一点，，点满足，求点的轨迹方程.
【解析】（1）由解得，则圆心为，半径为，
∴圆的标准方程为.
（2）设，.
由，可得，
则，又点在圆上，所以，
即，化简得，
∴点的轨迹方程为.
【变式6-4】（23-24高二上·广东广州·阶段练习）已知的三个顶点坐标分别是，，.求：
(1)外接圆的方程；
(2)若点P是外接圆上的一动点，点为平面内一定点，求线段MP的中点N的轨迹方程.
【解析】（1）由题意可作图如下：
由，则线段的中点坐标为，
线段的中垂线的斜率，
直线的方程为：；
同理可得线段的中垂线的方程：，
联立可得，解得，则直线与的交点，
显然点为外接圆的圆心，则该圆的半径，
所以外接圆的方程为：.
（2）由题意可作图如下：
设的坐标为，的坐标为，
由为的中点，且，则，整理可得，
由在圆上，则，
所以，化简可得：.
【变式6-5】（23-24高二上·河北保定·期末）已知点在圆上运动，，点为线段MN中点．
(1)求点的轨迹方程；
(2)已知，求的最大值．
【解析】（1）设点，因为为中点，
，于是有，
因为点在圆上运动，
所以，
代入得，
化简得，
所以点的轨迹方程为；
（2）
因为，所以
所以的最大值为89．
【变式6-6】（22-23高二上·江苏盐城·期末）已知圆的圆心在轴上，并且过，两点.
(1)求圆的方程；
(2)若为圆上任意一点，定点，点满足，求点的轨迹方程.
【解析】（1）由题意可知，的中点为，，所以的中垂线方程为，
它与轴的交点为圆心，又半径，所以圆的方程为；
（2）设，，由，得，
所以，又点在圆上，故，
所以，化简得的轨迹方程为