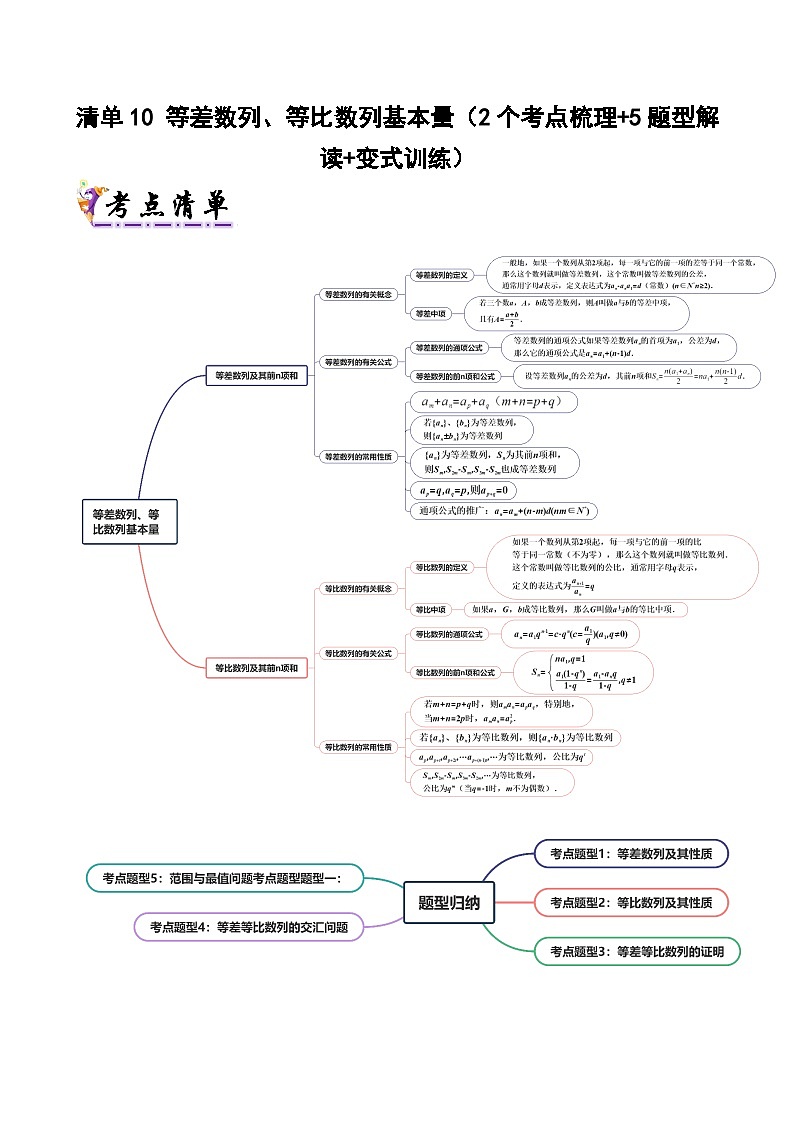
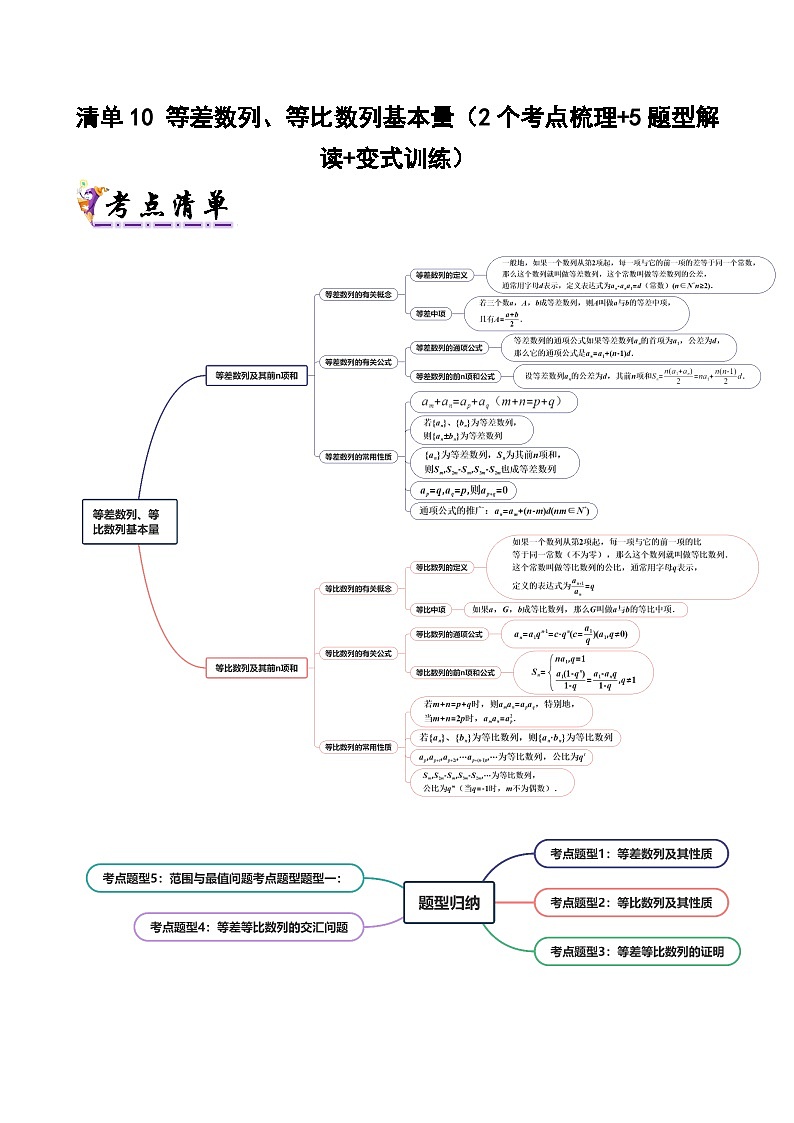
清单10 等差数列、等比数列基本量（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019）

这是一份清单10 等差数列、等比数列基本量（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019），文件包含清单10等差数列等比数列基本量清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019苏教版2019原卷版docx、清单10等差数列等比数列基本量清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019解析版docx等2份学案配套教学资源，其中学案共33页， 欢迎下载使用。

【清单01】等差数列
⑴定义：如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即－=d ，（n≥2，n∈N），
那么这个数列就叫做等差数列．
⑵等差中项：若三数成等差数列
⑶通项公式：
或
⑷前项和公式：
⑸常用性质：
①若，则；
②下标为等差数列的项，仍组成等差数列；
③数列（为常数）仍为等差数列；
④若、是等差数列，则、 （、是非零常数）、、，…也成等差数列．
⑤单调性：的公差为，则：
ⅰ）为递增数列；
ⅱ）为递减数列；
ⅲ）为常数列；
⑥数列{}为等差数列（p，q是常数）
⑦若等差数列的前项和，则、、… 是等差数列．
【清单02】等比数列
⑴定义：如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列．
⑵等比中项：若三数成等比数列（同号）．反之不一定成立．
⑶通项公式：
⑷前项和公式：
⑸常用性质
①若，则；
②为等比数列，公比为（下标成等差数列，则对应的项成等比数列）
③数列（为不等于零的常数）仍是公比为的等比数列；正项等比数列；则是公差为的等差数列；
④若是等比数列，则
是等比数列，公比依次是
⑤单调性：
为递增数列；为递减数列；
为常数列；
为摆动数列；
⑥既是等差数列又是等比数列的数列是常数列．
⑦若等比数列的前项和，则、、… 是等比数列．
考点题型1：等差数列及其性质
【典例1-1】（2024·高二·河南漯河·期末）等差数列中，，则其前100项和为（ ）
A．5050B．10010C．10100D．11000
【典例1-2】（2024·高二·河北保定·期末）若数列为等差数列，且，则等于（ ）
A．5B．4C．3D．2
【变式1-1】（2024·高二·云南昆明·期末）已知等差数列的前n项和为，若，则（ ）
A．20B．15C．10D．5
【变式1-2】（2024·高二·陕西渭南·期末）我国古代《洛书》中记载着一种三阶幻方：将九个数字填入一个的正方形方格，满足每行、每列、每条对角线上的三个数字之和相同（如图）．已知数列的通项公式为，现将该数列的前项填入一个的正方形方格，使其满足四阶幻方，则此四阶幻方中每一行的数字之和为（ ）

A．60B．72C．76D．80
【变式1-3】（2024·高二·湖南邵阳·期末）已知公差不为0的等差数列满足，则的最小值为（ ）
A．B．1C．D．2
【变式1-4】（2024·高二·西藏拉萨·期末）记为等差数列的前n项和，若，，则（ ）
A．B．C．D．
【变式1-5】（2024·高二·河南信阳·期末）数列满足，已知，则的前19项和（ ）
A．0B．8C．10D．19
考点题型2：等比数列及其性质
【典例2-1】（2024·高二·青海·期末）在等比数列中，，，则（ ）
A．64B．128C．D．
【典例2-2】（2024·高二·河北保定·期末）记为等比数列的前项和，若，，则（ ）
A．B．
C．D．
【变式2-1】（2024·高二·贵州黔南·期末）记为等比数列的前n项和，若，则（ ）
A．B．C．D．
【变式2-2】（2024·高二·江苏南京·期末）数列满足，则数列的前8项和为（ ）.
A．63B．127C．255D．256
【变式2-3】（2024·高二·云南保山·期末）设等比数列的前项的和为，若，则的近似值为（ ）
A．4B．3C．2D．
【变式2-4】（2024·高二·湖南益阳·期末）已知等比数列中，若，则（ ）
A．B．
C．D．
考点题型3：等差等比数列的证明
【典例3-1】（2024·高二·福建三明·期末）某企业2022年年初有资金5千万元，由于引进了先进生产设备，资金年平均增长率可达到50%，每年年底扣除下一年的消费基金千万元后，剩余资金投入再生产.设从2022年的年底起，每年年底企业扣除消费基金后的剩余资金依次为，，，…
(1)写出，，，并证明数列是等比数列；
(2)至少到哪一年的年底，企业的剩余资金会超过21千万元？
【典例3-2】（2024·高二·江苏南京·期末）设数列的前项和为，且，其中．
(1)证明为等差数列，求数列的通项公式；
(2)求数列的前项和
【变式3-1】（2024·高二·辽宁·期末）已知数列满足．
(1)证明是等比数列，并求的通项公式；
(2)证明：
【变式3-2】（2024·高二·湖南张家界·期末）已知数列是递增数列，其前项和满足.
(1)证明：是等差数列；
(2)记，数列的前项和为，求.
【变式3-3】（2024·高二·广东广州·期末）数列的首项，.
(1)证明是等差数列，并求的通项公式；
(2)设，
①当数列的项取得最大值时，求的值；
②求数列的前项和.
【变式3-4】（2024·高二·江西鹰潭·期末）已知数列的首项，且.
(1)证明：是等比数列.
(2)求数列的前n项和.
【变式3-5】（2024·高二·河南商丘·期末）在数列中，已知．
(1)证明：是等比数列，并求的通项公式；
(2)若，求数列的前项和Sn．
考点题型4：等差等比数列的交汇问题
【典例4-1】（2024·高二·陕西西安·期末）在等差数列中，，，且12是，的等比中项．
(1)求的通项公式；
(2)求数列的前n项和．
【典例4-2】（2024·高二·四川攀枝花·期末）已知数列的前项和为，且满足，公差不为0的等差数列中，，且是与的等比中项.
(1)求数列的通项公式；
(2)求数列的前项和.
【变式4-1】（2024·高二·安徽滁州·期末）已知公差不为0的等差数列，其前项和为.若，且成等比数列.
(1)求数列的通项公式；
(2)若，求数列的前项和.
【变式4-2】（2024·上海长宁·一模）已知数列是公差为2的等差数列，数列为等比数列．
(1)若，，，求数列的通项公式：
(2)设数列的前n项和为，若，，求．
【变式4-3】（2024·高二·山东日照·期中）已知公差为正数的等差数列的前项和为，数列为等比数列，且，.
(1)求数列的前项和；
(2)设，求数列的前项和.
考点题型5：范围与最值问题
【典例5-1】（2024·高二·辽宁本溪·期中）已知等比数列的前项和为，若恒成立，则的最小值为（ ）
A．B．C．D．1
【典例5-2】（2024·高二·辽宁·阶段练习）设数列的前项和为，则下列说法正确的是（ ）
A．是等比数列
B．成等差数列，公差为
C．当且仅当时，取得最大值
D．时，的最大值为33
【变式5-1】（多选题）（2024·高二·四川乐山·期末）已知等差数列的公差为d，前n项和为，若，，则下列说法正确的是（ ）
A．B．C．D．最小值为
【变式5-2】（多选题）（2024·高二·四川成都·期末）已知数列的通项公式为 ，前 项积为 ，则下列说法正确的是（ ）
A．在数列中，是最大项B．在数列中， 是最小项
C．数列单调递减D．使取得最小值的为 9
【变式5-3】（多选题）（2024·高二·安徽滁州·期末）已知等差数列的前项和为，公差，且，则下列说法正确的是（ ）
A．B．
C．当取得最小值时，的值为22D．当时，的最小值为44
【变式5-4】（多选题）（2024·高二·内蒙古·期末）已知公比为的正项等比数列的前项积为，则（ ）
A．
B．当时，
C．
D．当，且取得最小值时，只能等于6
【变式5-5】（多选题）（2024·高二·陕西渭南·期末）设等比数列的公比为，其前项和为，前项积为，若，，且，则下列结论正确的是（ ）
A．B．
C．数列中的最大值是D．数列无最大值