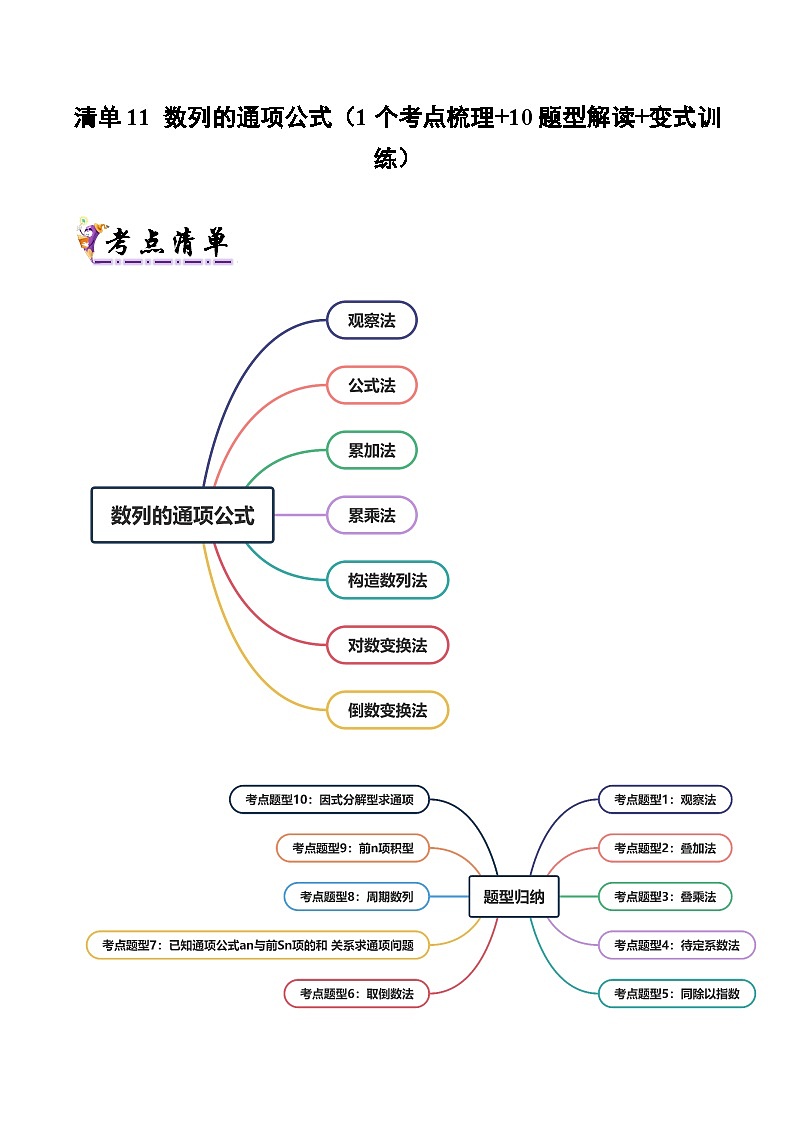
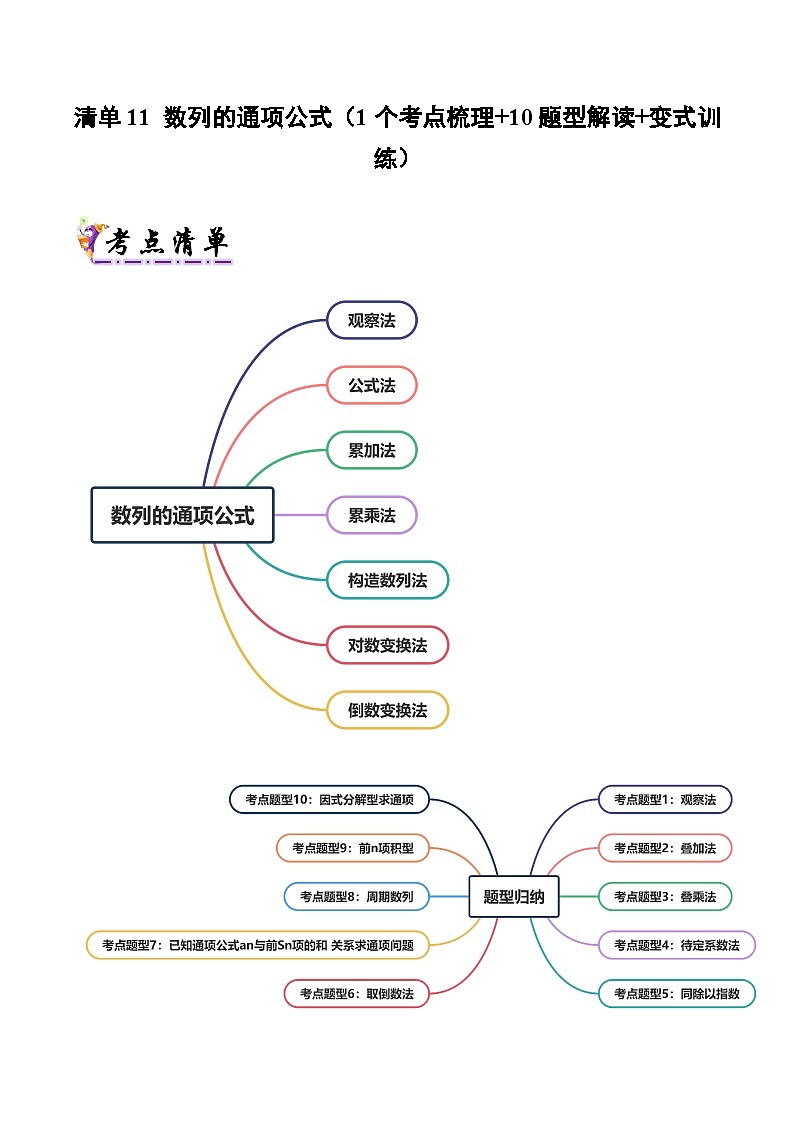
清单11 数列的通项公式（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019）

这是一份清单11 数列的通项公式（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019），文件包含清单11数列的通项公式清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019原卷版docx、清单11数列的通项公式清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019解析版docx等2份学案配套教学资源，其中学案共41页， 欢迎下载使用。

【清单01】数列的通项公式
类型Ⅰ观察法：
已知数列前若干项，求该数列的通项时，一般对所给的项观察分析，寻找规律，从而根据规律写出此数列的一个通项．
类型Ⅱ公式法：
若已知数列的前项和与的关系，求数列的通项可用公式构造两式作差求解．
用此公式时要注意结论有两种可能，一种是“一分为二”，即分段式；另一种是“合二为一”，即和合为一个表达，（要先分和两种情况分别进行运算，然后验证能否统一）．
类型Ⅲ累加法：
形如型的递推数列（其中是关于的函数）可构造：
将上述个式子两边分别相加，可得：
= 1 \* GB3 ①若是关于的一次函数，累加后可转化为等差数列求和；
= 2 \* GB3 ②若是关于的指数函数，累加后可转化为等比数列求和；
= 3 \* GB3 ③若是关于的二次函数，累加后可分组求和；
= 4 \* GB3 ④若是关于的分式函数，累加后可裂项求和．
类型Ⅳ累乘法：
形如型的递推数列（其中是关于的函数）可构造：
将上述个式子两边分别相乘，可得：
有时若不能直接用，可变形成这种形式，然后用这种方法求解．
类型Ⅴ构造数列法：
㈠形如（其中均为常数且）型的递推式：
（1）若时，数列{}为等差数列；
（2）若时，数列{}为等比数列；
（3）若且时，数列{}为线性递推数列，其通项可通过待定系数法构造等比数列来求．方法有如下两种：
法一：设，展开移项整理得，与题设比较系数（待定系数法）得，即构成以为首项，以为公比的等比数列．再利用等比数列的通项公式求出的通项整理可得
法二：由得两式相减并整理得即构成以为首项，以为公比的等比数列．求出的通项再转化为类型Ⅲ（累加法）便可求出
㈡形如型的递推式：
⑴当为一次函数类型（即等差数列）时：
法一：设，通过待定系数法确定的值，转化成以为首项，以为公比的等比数列，再利用等比数列的通项公式求出的通项整理可得
法二：当的公差为时，由递推式得：，两式相减得：，令得：转化为类型Ⅴ㈠求出，再用类型Ⅲ（累加法）便可求出
⑵当为指数函数类型（即等比数列）时：
法一：设，通过待定系数法确定的值，转化成以为首项，以为公比的等比数列，再利用等比数列的通项公式求出的通项整理可得
法二：当的公比为时，由递推式得：——①，，两边同时乘以得——②，由①②两式相减得，即，在转化为类型Ⅴ㈠便可求出
法三：递推公式为（其中p，q均为常数）或（其中p，q，r均为常数）时，要先在原递推公式两边同时除以，得：，引入辅助数列（其中），得：再应用类型Ⅴ㈠的方法解决．
⑶当为任意数列时，可用通法：
在两边同时除以可得到，令，则，在转化为类型Ⅲ（累加法），求出之后得．
类型Ⅵ对数变换法：
形如型的递推式：
在原递推式两边取对数得，令得：，化归为型，求出之后得（注意：底数不一定要取10，可根据题意选择）．
类型Ⅶ倒数变换法：
形如（为常数且）的递推式：两边同除于，转化为形式，化归为型求出的表达式，再求；
还有形如的递推式，也可采用取倒数方法转化成形式，化归为型求出的表达式，再求．
类型Ⅷ形如型的递推式：
用待定系数法，化为特殊数列的形式求解．方法为：设，比较系数得，可解得，于是是公比为的等比数列，这样就化归为型．
总之，求数列通项公式可根据数列特点采用以上不同方法求解，对不能转化为以上方法求解的数列，可用归纳、猜想、证明方法求出数列通项公式
考点题型1：观察法
【典例1-1】（2024·高二·安徽·期末）数列的通项公式可以为（ ）
A．B．
C．D．
【答案】B
【解析】对于选项A：令，可得，不合题意；
对于选项B：代入检验均可，符合题意；
对于选项C：令，可得，不合题意；
对于选项D：令，可得，不合题意；
故选：B.
【典例1-2】（2024·高二·江西景德镇·期末）数列的通项公式可能是（ ）
A．B．
C．D．
【答案】D
【解析】由题数列的前5项可改写为，
其中负号交替出现在偶数项，分母为从1开始的奇数，
故数列的通项公式为.
故选：D.
【变式1-1】（2024·高二·广东佛山·期中）将自然数1，2，3，4，5，……，按照如图排列，我们将2，4，7，11，16，……都称为“拐角数”，则下列哪个数不是“拐角数”．（ ）
A．22B．30C．37D．46
【答案】B
【解析】由题意得第1个“拐角数”为，第2个“拐角数”为，
第3个“拐角数”为，第4个“拐角数”为，
则第个“拐角数”为．
对于A：第6个“拐角数”是，故A不合题意；
对于B、C：第7个“拐角数”是，第8个“拐角数”是，
则30不是“拐角数”，故B适合题意，C不合题意；
对于D：第9个“拐角数”是，故D不合题意．
故选：B.
【变式1-2】（2024·高二·福建福州·期中）已知数列的前项依次为，则的一个通项公式是（ ）
A．B．
C．D．
【答案】B
【解析】数列的前项依次为，
即，
所以的一个通项公式为．故B正确；
对A，代入，，故A错误；
对C，，故C错误；
对D，，故D错误；
故选：B.
【变式1-3】（2024·高二·福建福州·期末）数列的一个通项公式为（ ）
A．B．C．D．
【答案】B
【解析】由数列，可得化为，
可得数列的一个通项公式为.
故选：C.
考点题型2：叠加法
【典例2-1】（2024·高二·上海宝山·期末）在数列中，，且，则 .
【答案】5
【解析】
，
，
…
，
各式累加得.
故答案为：5.
【典例2-2】（2024·高二·湖南常德·开学考试）已知数列满足，，则 ．
【答案】
【解析】若，则，即，这与矛盾，所以，
由两边同时除以，得，
则，，，，
上面的式子相加可得：，
所以，
故答案为：.
【变式2-1】（2024·高二·福建漳州·期末）数列满足，且，则数列的通项公式 ．
【答案】
【解析】
，该通式对也适用，
所以答案为：.
【变式2-2】（2024·高二·山东滨州·期末）已知数列中，，则 .
【答案】
【解析】由题意可知：，，，，
将上述个式子相加可得：，则，所以
故答案为：
【变式2-3】（2024·高二·广东深圳·期末）已知数列满足：，，则数列的通项公式为 .
【答案】
【解析】由题意知数列满足：，，
故
，,
也适合该式，故，
故答案为：
考点题型3：叠乘法
【典例3-1】（2024·高二·广东河源·期末）已知正项数列满足，则 .
【答案】
【解析】由可得，
由累乘可得.
故答案为：
【典例3-2】（2024·高二·内蒙古·期末）在数列中，，则 ．
【答案】
【解析】因，故有，即得，
所以．
故答案为：.
【变式3-1】（2024·高三·辽宁葫芦岛·期末）在数列中，，，则数列的通项公式为 .
【答案】
【解析】因为，
所以，
所以，，，……，，，
所以，
所以，
因为，所以符号该式，
故答案为：
【变式3-2】（2024·高二·海南海口·期中）已知数列的前项和为且满足，则数列的通项公式为 ．
【答案】
【解析】当时，，
化简得，，利用累乘法得
，
显然满足上式，
所以
故答案为：
【变式3-3】（2024·高二·北京·期中）数列中，若，，则 .
【答案】
【解析】由题意，，可得，所以，
所以.
故答案为：.
考点题型4：待定系数法
【典例4-1】（2024·高三·广东·阶段练习）在数列中，，且，则的通项公式为 ．
【答案】
【解析】因为，设，其中、，
整理可得，
所以，，解得，所以，，
且，所以，数列是首项为，公比也为的等比数列，
所以，，解得.
故答案为：.
【典例4-2】（2024·高二·广东深圳·期末）已知数满足，则数列的通项公式 ．
【答案】
【解析】由可得：，又,
，
所以是以为首项，为公比的等比数列，
所以，所以.
故答案为：
【变式4-1】（2024·高二·福建福州·期末）数列中，，，则此数列的通项公式 .
【答案】
【解析】因为，所以，又，
所以，所以是以为首项，为公比的等比数列，
所以，则.
故答案为：
【变式4-2】（2024·高三·安徽合肥·阶段练习）已知数列中，（），则数列的通项公式 .
【答案】
【解析】因为，故可得，
故可得数列是首项为3公比为3的等比数列，
则，解得.
故答案为：.
【变式4-3】（2024·高二·广东佛山·阶段练习）已知数列满足，且，若，则（ ）
A．253B．506C．1012D．2024
【答案】B
【解析】因为，所以.
因为，所以，故为常数列，
所以. 由，解得.
故选：B
【变式4-4】（2024·高二·河北沧州·阶段练习）已知数列满足，，则该数列的通项公式 ．
【答案】
【解析】因为，所以，则数列时以为首项
公比为的等比数列，故，所以.
【变式4-5】（2024·高二·宁夏中卫·阶段练习）数列满足且，则数列的通项公式是 ．
【答案】
【解析】设，则，
又因为，所以，则，
所以，
因为，所以，
所以为常数，
所以是首项为，公比为的等比数列，
所以，所以.
故答案为：
【变式4-6】（2024·高三·全国·对口高考）已知数列中，，且（，且），则数列的通项公式为 ．
【答案】
【解析】由，得，即
由所以，
于是数列是以首项为，公比为的等比数列，
因此，即，
当时，,此式满足，
所以数列的通项公式为.
故答案为：.
考点题型5：同除以指数
【典例5-1】（2024·高二·河北石家庄·期末）已知数列满足，且，则数列的通项公式 ．
【答案】
【解析】∵，
∴，
即．又，，
∴数列是以3为首项，1为公差的等差数列，
∴，
∴数列的通项公式．
故答案为：.
【典例5-2】（2024·高二·山东淄博·期中）已知数列满足，，则数列的通项公式为
【答案】
【解析】由得，
故为等差数列，公差为1，首项为1，
所以
所以.
故答案为：
【变式5-1】（2024·云南·二模）记数列的前项和为，若，则 .
【答案】/0.5
【解析】由，得，
则，
又，则，则，
，，
，
故答案为：.
【变式5-2】（2024·高二·四川南充·期中）已知数列的首项为，且满足，则 ．
【答案】
【解析】由，即，
则，又，
故数列是以为公比、为首项的等比数列，
即，则.
故答案为：.
【变式5-3】（2024·高三·全国·专题练习）已知正项数列中，，则数列的通项（ ）
A．B．
C．D．
【答案】D
【解析】解法一：在递推公式的两边同时除以，得①，
令，则①式变为，即，
所以数列是等比数列，其首项为，公比为，
所以，即，
所以，
所以，
解法二：设，则，
与比较可得，
所以，
所以数列是首项为，公比为2的等比数列，
所以，所以，
故选：D
考点题型6：取倒数法
【典例6-1】（2024·高二·陕西西安·期中）已知数列满足，，，则（ ）
A．B．C．D．
【答案】D
【解析】，即，
可得，又，
即有数列是首项为1，公差为4的等差数列，
可得，
即.
故选：D.
【典例6-2】（2024·高二·全国·单元测试）已知数列满足，，，则 .
【答案】
【解析】数列中，，，显然，取倒数得，
即，则数列是首项为1，公差为4的等差数列，
因此，所以.
故答案为：.
【变式6-1】（2024·高二·湖北荆州·期末）已知数列，则数列的通项公式 ．
【答案】
【解析】由题意得，故是首项为1，公差为1的等差数列，
得，即，
故答案为：
【变式6-2】（2024·高二·河南·期中）数列中，若，，则 ．
【答案】19
【解析】∵，则，
∴，∴故数列为等差数列，公差等于2，
又，故，
∴.
故答案为：19．
考点题型7：已知通项公式与前项的和关系求通项问题
【典例7-1】（2024·高二·云南昆明·期末）已知数列的前n项和，则数列的通项公式为
【答案】
【解析】数列的前n项和，
当时，，
而，不满足上式，
所以数列的通项公式为.
故答案为：
【典例7-2】（2024·高三·四川·期末）若数列的前n项和为，，，则数列的通项公式为 ．
【答案】
【解析】数列中，，当时，，
两式相减得，即，则有，
因此数列是常数列，则，
所以数列的通项公式为.
故答案为：
【变式7-1】（2024·高二·江苏宿迁·期末）已知数列的前项和为，，（），则为 .
【答案】
【解析】数列的前项和，当时，，
整理得，即，显然当时，数列是常数列，
因此，所以.
故答案为：
【变式7-2】（2024·高二·山东青岛·期末）设数列 满足 ， 则 的通项公式
【答案】
【解析】数列 满足，
设，
当时，有，即，
当时，有，得，
不符合，
所以.
故答案为：.
【变式7-3】（2024·高二·福建福州·期末）设数列的前项和为.已知，数列的通项公式 .
【答案】
【解析】因为，则当时，，
两式相减得：，即，
而，
则数列是以1为首项，4为公比的等比数列，
所以数列的通项公式是.
故答案为：.
【变式7-4】（2024·高三·上海虹口·阶段练习）记为数列的前项和，且，则 .
【答案】
【解析】①，当时，，解得，
当时，②，
①-②得，，
即，所以，
是首项为-1，公比是2的等比数列，故.
故答案为：
【变式7-5】（2024·高二·新疆阿克苏·期末）已知数列的前n项和，.
(1)写出数列的通项公式.
(2)证明：数列是等差数列；
【解析】（1）当时，，
当时，，满足，
即数列的通项公式．
（2），
当时，为常数，
则数列是等差数列．
【变式7-6】（2024·高二·贵州遵义·期末）数列的前n项和记为，已知，．
(1)求证：是等差数列；
(2)若，，成等比数列，求的最大值．
【解析】（1）①，
当时， ②，
得：，
即，即，且.
是公差为的等差数列.
（2）由（1）知是公差为的等差数列，
，
又，，成等比数列，
，
，即，
故，解得.
，
，
二次函数的对称轴为，
，当或时取到最大值为.
故的最大值为.
考点题型8：周期数列
【典例8-1】（2024·高二·江苏盐城·期中）若数列满足，若，则的值为
【答案】
【解析】由已知，则，，
可得，进而可得，，，
即，，
所以，
故答案为：.
【典例8-2】（2024·高二·江苏·期中）已知数列满足，，，则 ．
【答案】
【解析】由已知，则，
且，
所以，
故答案为：.
【变式8-1】（2024·高二·浙江杭州·期末）已知数列满足，若，则 ．
【答案】
【解析】因为的最小正周期为，且余，
由已知可得，
故答案为：.
【变式8-2】（2024·高二·上海·期末）数列满足：，则 .
【答案】/0.5
【解析】法一：依次代入的值，看看它们符合什么规律：
.至此可以发现周期为3.
（余数为2），.
故答案为：.
法二：该数列的周期为3，推理过程如下展示：
将换成，得，再将代入，得
，
再将换成，得，继续将代入，得，
，以下同解法一.
故答案为：.
【变式8-3】（2024·高二·福建福州·期末）数列满足，则 ．
【答案】
【解析】，
，
.至此可以发现该数列的周期为3.
（余数为2），.
故答案为：.
考点题型9：前n项积型
【典例9-1】（2024·高二·山西长治·期末）已知数列满足，则的通项公式 .
【答案】
【解析】因为，
若，可得；
若，则，
可得；
且符合上式，可得，所以.
故答案为：.
【典例9-2】（2024·高二·河南郑州·期末）设正数数列的前项和为，数列的前项积为，且，则（ ）
A．B．C．D．
【答案】B
【解析】当时，，解得：；
当时，由得：，即，
，
数列是以为首项，为公差的等差数列，
，解得：，，
经检验：满足，，
故选：B.
【变式9-1】（2024·高二·江苏镇江·阶段练习）记为数列的前n项积，已知，则（ ）
A．23B．24C．25D．26
【答案】C
【解析】因为为数列的前n项积，
当时，，所以，∴，
当时，，所以，
化简可得：，
所以是以为首项，为公差的等差数列，
所以.
所以.
故选：C.
【变式9-2】（2024·河南开封·三模）记为数列的前n项和，为数列的前n项积，若，，则满足的n的最小值是（ ）
A．5B．6C．7D．8
【答案】B
【解析】由可得，，
故为公比为2的等比数列，故，
所以，故，
因此
故，
要使，则，
当时，，时，，且在时，随着正整数的增大而增大，故的最小值为6，
故选：B
【变式9-3】（2024·高二·山东威海·期末）设为数列的前n项和，为数列的前n项积，已知．
(1)求，；
(2)求证：数列为等差数列；
(3)求数列的通项公式．
【解析】（1）由，且，
当时，，得，
当时，，得；
（2）对于①，
当时，②，
①②得，
即，，
又，
数列是以1为首项，1为公差的等差数列；
（3）由（2）得，
，
当时，，
又时，，不符合，
.
【变式9-4】（2024·高二·湖南永州·期末）设数列的前项之积为，且满足．
(1)证明：数列是等差数列，并求数列的通项公式；
(2)记，证明：．
【解析】（1）方法一：当，得，
当时，①
②
两式相除可得：
即，又，
故，
变形为：，
因为，所以是以为首项，1为公差的等比数列．
所以
化简可得
法二：因为，，
所以
即
令，则，
所以以3为首项，以2为公差的等差数列，
所以，即，
所以．
又因为满足上式，
所以，
所以，故，
故数列是等差数列．
（2）
因为，
所以
考点题型10：因式分解型求通项
【典例10-1】（2024•安徽月考）已知正项数列满足：，，．
（Ⅰ）判断数列是否是等比数列，并说明理由；
（Ⅱ）若，设．，求数列的前项和．
【解析】解：（Ⅰ），，
又数列为正项数列，
，
①当时，数列不是等比数列；
②当时，，此时数列是首项为，公比为2的等比数列．
（Ⅱ）由（Ⅰ）可知：，
，
．
【典例10-2】（2024•怀化模拟）已知正项数列满足，设．
（1）求，；
（2）判断数列是否为等差数列，并说明理由；
（3）的通项公式，并求其前项和为．
【解析】解：（1），，，
可得，
则，
数列为首项为1，公比为2的等比数列，
可得；
，
，；
（2）数列为等差数列，理由：，
则数列为首项为0，公差为1的等差数列；
（3），
前项和为．
【变式10-1】（2024•仓山区校级月考）已知正项数列满足且
（Ⅰ）证明数列为等差数列；
（Ⅱ）若记，求数列的前项和．
【解析】证明：由，
变形得：，
由于为正项数列，，
利用累乘法得：从而得知：数列是以2为首项，以2为公差的等差数列．
（Ⅱ）解：由（Ⅰ）知：，
从而．