清单12 数列求和（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019）

这是一份清单12 数列求和（清单 导图 考点 题型 变式 ）学案-2024-2025学年高二数学上学期期末考点（苏教版2019），文件包含清单12数列求和清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019原卷版docx、清单12数列求和清单导图考点题型变式-2024-2025学年高二数学上学期期末考点苏教版2019解析版docx等2份学案配套教学资源，其中学案共42页， 欢迎下载使用。

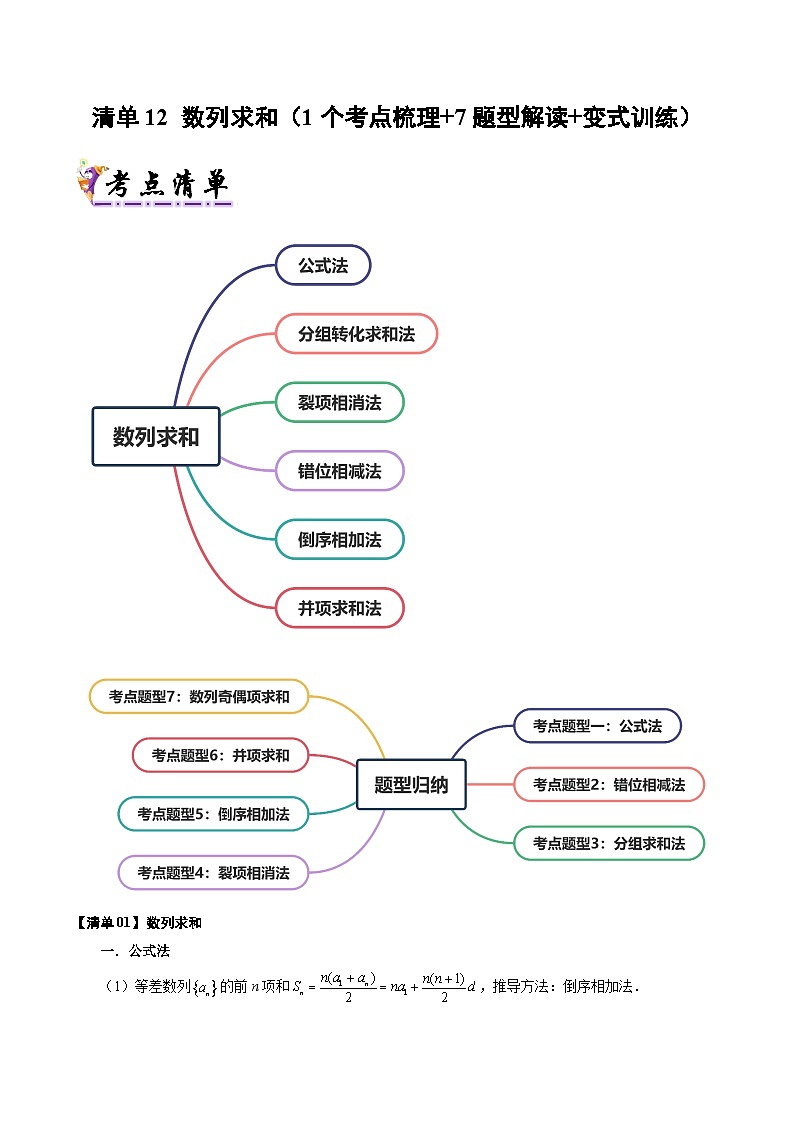
【清单01】数列求和
一．公式法
（1）等差数列的前n项和，推导方法：倒序相加法．
（2）等比数列的前n项和，推导方法：乘公比，错位相减法．
（3）一些常见的数列的前n项和：
①；
②；
③；
= 4 \* GB3 \* MERGEFORMAT ④
二．几种数列求和的常用方法
（1）分组转化求和法：一个数列的通项公式是由若干个等差或等比或可求和的数列组成的，则求和时可用分组求和法，分别求和后相加减．
（2）裂项相消法：把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得前n项和．
（3）错位相减法：如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么求这个数列的前项和即可用错位相减法求解．
（4）倒序相加法：如果一个数列与首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前项和即可用倒序相加法求解．
三．常见的裂项技巧
积累裂项模型1：等差型
（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
（9）
（10）
（11）
（12）
积累裂项模型2：根式型
（1）
（2）
（3）
（4）
（5）
（6）
积累裂项模型3：指数型
（1）
（2）
（3）
（4）
（5）
（6），设，易得，
于是
（7）
积累裂项模型4：对数型
积累裂项模型5：三角型
（1）
（2）
（3）
（4），
则
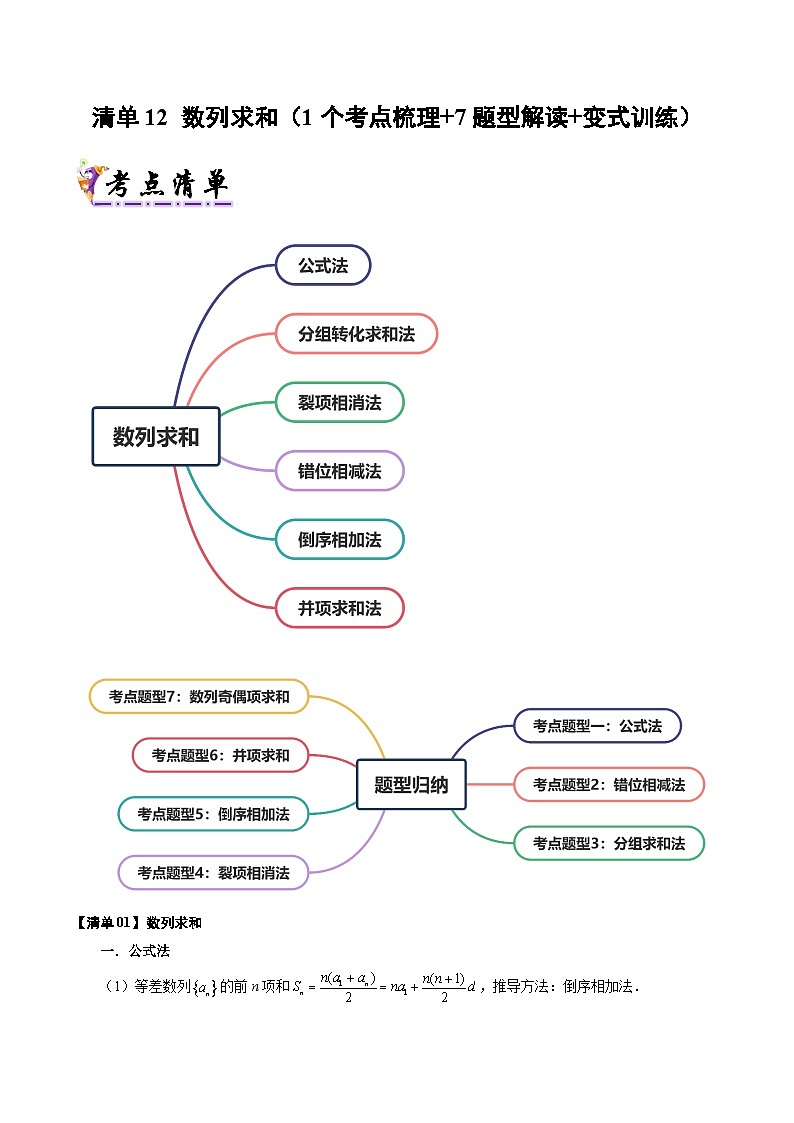
考点题型一：公式法
【典例1-1】（2024·河北邢台·高二校联考阶段练习）已知是各项均为正数的等比数列，.
(1)求的通项公式；
(2)设，求数列的前项和.
【典例1-2】（2024·湖南·高二校联考期中）等差数列满足，，前项和为.
(1)求数列的通项公式；
(2)求的最大值.
【变式1-1】（2024·浙江温州·高二乐清市知临中学校考期中）等差数列满足：首项为2，公差为是的前项和.
(1)求数列的通项公式.
(2)求数列的前项和.
考点题型2：错位相减法
【典例2-1】（2024·高二·湖南·期末）数列的前项和为，当时，，数列满足：.
(1)证明：数列是等比数列；
(2)记数列，数列的前项和为，求.
【典例2-2】（2024·高二·江苏南京·期末）设数列的前项和为，且，其中．
(1)证明为等差数列，求数列的通项公式；
(2)求数列的前项和
【变式2-1】（2024·高二·江西新余·期末）已知公差大于0的等差数列和公比大于0的等比数列满足.
(1)求数列和的通项公式；
(2)记数列的前项和为，求证：.
【变式2-2】（2024·高二·辽宁·期末）已知数列满兄，，数列的前项和为，且．
(1)求数列，的通项公式，
(2)求数列的前项和为．
【变式2-3】（2024·高二·福建·期中）设数列满足，.
(1)求数列的通项公式；
(2)令，求数列的前项和.
【变式2-4】（2024·高二·江苏南通·期中）已知等比数列的前项和为，且．
(1)求；
(2)若，求数列的前项和．
考点题型3：分组求和法
【典例3-1】（2024·高二·山东青岛·期中）已知数列为等差数列，首项，公差，．
(1)证明是等比数列；
(2)求数列的前项和．
【典例3-2】（2024·高二·福建莆田·期中）已知正项等差数列满足：且成等比数列.
(1)求数列的通项公式：
(2)若数列为递增数列，数列满足：，求数列的前项和.
【变式3-1】（2024·高二·上海·期中）在数列中，，．
(1)求数列的通项公式；
(2)若，求数列的前n项和．
【变式3-2】（2024·高二·湖南永州·期中）已知等差数列满足，.
(1)求数列的通项公式；
(2)设，求数列的前项和.
【变式3-3】（2024·高二·福建福州·期末）设为数列的前项和，已知，.
(1)求证：是等差数列；
(2)求数列的前项和.
【变式3-4】（2024·高二·辽宁辽阳·期末）设依次是等比数列的前3项，其中为正数.
(1)求；
(2)求数列的前项和.
考点题型4：裂项相消法
【典例4-1】（2024·高二·河南漯河·期末）已知数列满足：，.
(1)若，求证：为等差数列.
(2)求数列的前项和.
【典例4-2】（2024·高二·云南昆明·期末）已知数列满足，．
(1)求证：是等差数列，并求的通项公式；
(2)记，求．
【变式4-1】（2024·高二·四川德阳·期末）数列的前n项和为，且.
(1)求证：数列为等比数列，并求其通项公式；
(2)令，数列的前n项和为.求证：.
【变式4-2】（2024·高二·江苏·期中）已知数列的前项和为，且满足．
(1)求数列的通项公式．
(2)已知，求数列的最大项，以及取得最大项时的值．
(3)已知，求数列的前项和．
【变式4-3】（2024·高二·江苏苏州·期中）已知数列和数列，为数列的前项和，，，.
(1)求数列和数列的通项公式；
(2)若数列满足，求数列的前项和
考点题型5：倒序相加法
【典例5-1】（2024·高二·福建泉州·期末）已知数列是公比为的正项等比数列，且，若，则（ ）
A．B．C．D．
【典例5-2】（2024·高二·江苏常州·期末）已知函数满足，若数列满足，则数列的前16项的和为 .
【变式5-1】（2024·高三·湖北鄂州·期末）设函数，定义，其中，，则 .
【变式5-2】（2024·高二·江苏无锡·期中）对于三次函数，给出定义：设是函数的导数，是函数的导数，若方程有实数解，则称点为函数的“拐点”.某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心.给定函数，请你根据上面的探究结果，解答以下问题：
①函数的对称中心坐标为 ；
②计算 .
【变式5-3】（2024·高二·安徽六安·期末）已知函数，数列是正项等比数列，且，则 ．
考点题型6：并项求和
【典例6-1】（2024·高二·广西南宁·期末）已知数列满足，则其前9项和 .
【典例6-2】（2024·高二·河南南阳·期中）已知数列满足，且前12项和为134，则 ．
【变式6-1】（2024·高二·河南焦作·期末）已知数列满足，则的前100项和为（ ）
A．2475B．2500C．2525D．5050
【变式6-2】（2024·高二·山东潍坊·期中）记数列的前n项和为，若，则（ ）
A．301B．101C．D．
【变式6-3】（2024·高二·湖北武汉·期末）在数列中，，且.
(1)求的通项公式；
(2)令，求数列的前项和.
【变式6-4】（2024·高二·江苏·期中）已知数列是等差数列，且恒成立，它的前四项的平方和为54，且这四项中首尾两数的积比中间两数的积少2．
(1)求的通项公式．
(2)若，，求数列的前100项和．
【变式6-5】（2024·高二·江苏·期中）已知等差数列的前项和为，满足，．
(1)求数列的通项公式；
(2)设，求．
考点题型7：数列奇偶项求和
【典例7-1】（2024·高二·广东广州·期末）设数列 的前 项和为 ，已知，且成等差数列.
(1)求 的通项公式；
(2)设求数列 的前 项和 .
【典例7-2】（2024·高二·云南保山·期末）已知的前项和是，且．
(1)求数列的通项公式；
(2)设求数列的前项和．
【变式7-1】（2024·高二·江苏常州·期末）在数列中，，且对任意的，都有.
(1)证明：是等比数列，并求出的通项公式；
(2)若，求数列的前项和.
【变式7-2】（2024·高二·湖南·期末）已知正项数列的前n项和为，且.
(1)求，的值及数列的通项公式；
(2)求数列的最大项；
(3)若数列满足，求数列的前30项和（，）.
【变式7-3】（2024·高二·江苏盐城·期末）已知等差数列的首项为1，公差.数列为公比的等比数列，且成等差数列.
(1)求数列和数列的通项公式；
(2)若，求数列的前项和.
【变式7-4】（2024·高二·山东临沂·期末）已知为等差数列，，记分别为数列的前项和，.
(1)求的通项公式;
(2)求.