

初中数学北师大版(2024)八年级下册第一章 三角形的证明3 线段的垂直平分线课时训练
展开
这是一份初中数学北师大版(2024)八年级下册第一章 三角形的证明3 线段的垂直平分线课时训练,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题
1.在△ABC的BC边上找一点P,使得PA+PC=BC.下面找法正确的是( )
A.B.
C.D.
2.如图,在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是( )
A.15°B.20°C.30°D.25°
3.如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC长为8cm,BE长为6cm,则EC的长为( )
A.4cmB.3cmC.2cmD.1cm
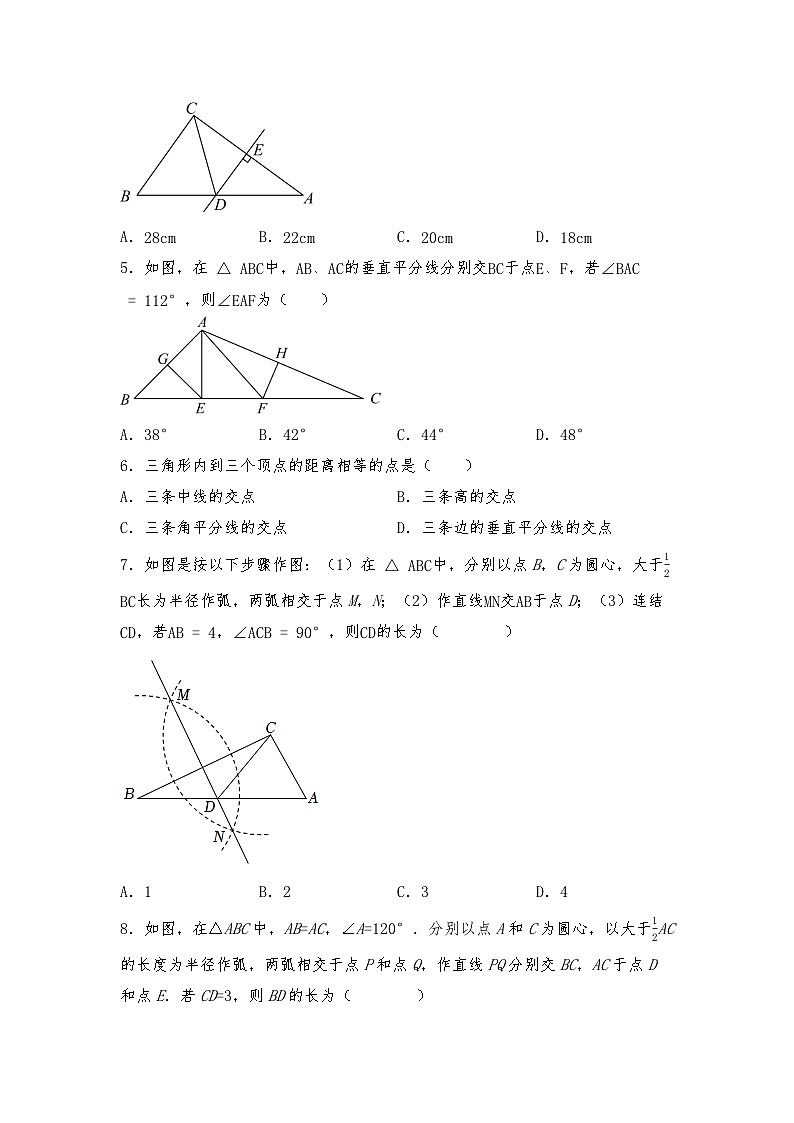
4.如图,直线DE是△ABC边AC的垂直平分线,且与AC相交于点E,与AB相交于点D,连接CD,已知BC=12cm,AB=16cm,则△BCD的周长为( )
A.28cmB.22cmC.20cmD.18cm
5.如图,在△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若∠BAC=112°,则∠EAF为( )
A.38°B.42°C.44°D.48°
6.三角形内到三个顶点的距离相等的点是( )
A.三条中线的交点B.三条高的交点
C.三条角平分线的交点D.三条边的垂直平分线的交点
7.如图是按以下步骤作图:(1)在△ABC中,分别以点B,C为圆心,大于12BC长为半径作弧,两弧相交于点M,N;(2)作直线MN交AB于点D;(3)连结CD,若AB=4,∠ACB=90°,则CD的长为( )
A.1B.2C.3D.4
8.如图,在△ABC中,AB=AC,∠A=120°.分别以点A和C为圆心,以大于12AC的长度为半径作弧,两弧相交于点P和点Q,作直线PQ分别交BC,AC于点D和点E.若CD=3,则BD的长为( )
A.4B.5C.6D.7
9.如图,在△ABC中,分别以A,C为圆心,大于12AC长为半径作弧,两弧分别相交于M,N两点,作直线MN,分别交线段BC,AC于点D,E,若AE=2cm,△ABD的周长为11cm,则△ABC的周长为( )
A.13cmB.14cmC.15cmD.16cm
二、填空题
1.如图,D、E是△ABC的BC边上的两点,DM,EN分别垂直平分AB、AC,垂足分别为点M、N.若∠DAE=24°,则∠BAC的度数为_______.
2.在△ABC中,∠C=90°,DE是AB的垂直平分线,∠A=40°,则∠CDB=______.
3.如图,在△ABC中,∠C=90°,∠A=15°,斜边AB的垂直平分线交AC于点E,交AB于点D,AE=8cm,则BC=______cm.
4.如图所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为_______.
5.如图,在△ABC中,AB=AC=5,BC=6,AD是∠BAC的平分线,AD=4.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是_____.
三、解答题
1.如图,直线m表示一条公路,A,B表示两所大学,要在公路旁修建一个车站P,使车站到两所大学的距离相等.请用尺规在图上找出点P并说明理由.
2.如图,在△ABC中,AD平分∠BAC交BC于点D,∠B=60°,∠C=26°.
(1)请用无刻度的直尺和圆规作出线段AC的垂直平分线;(要求:不写作法,保留作图痕迹,使用2B铅笔作图)
(2)记(1)中所作AC的垂直平分线交BC于点E,交AC于点F,连接AE.求∠DAE的度数.
3.如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:
(1)BC=AD;
(2)点O在线段AB的垂直平分线上.
4.如图,AC=AB,DC=DB,AD与BC相交于O.
(1)求证:△ACD≌△ABD;
(2)求证:AD垂直平分BC.
5.如图,已知Rt△ABC中,∠ACB=90°,AB=8,BC=5.
(1)作BC的垂直平分线,分别交AB、BC于点D、H;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接CD,求△BCD的周长.
6.(1)如图,已知△ABC,P为边AB上一点,请用尺规作图的方法在边AC上求作一点E.使AE+EP=AC.(保留作图痕迹,不写作法)
(2)在上图中,如果AC=6cm,AP=3cm,则△APE的周长是_______cm.
7.已知,△CBD中,CB=CD,点E是△ABD的边AB上的点,且CE⊥BD于H.
(1)如图1,若DE∥BC,求证:BE=BC.
(2)如图2,DE与BC不平行,连接AC,交BD于点F.若DE恰好垂直平分AC,且AF=AE.请先找出图中所有与BE相等的线段(不需另填字母),再进行证明.
8.如图,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于点H,分别交直线AB、AC、BC于点N、E、M.
(1)如图1,当点M与点C重合时,求证:BN=CD;
(2)如图2,当点M在BC的延长线上时,BN、CE、CD之间具有怎样的数量关系?并说明理由.
9.如图,在等边△ABC中,D为BC边的中点,点E为线段AD上一点,连接CE,以CE为边构造等边△CEF(点B,E,F不共线),连接AF,BF.
(1)求证:BF垂直平分AC;
(2)如图2,作CE关于直线AC对称的线段CE',连接E'F,猜想E'F与BC的位置关系并说明理由.
答案
一、选择题
D..D.B.C.C.
二、填空题
1.102°. 2.80°.3.4. 4.15. 5.245.
三、解答题
1.解:如图所示,点P是AB的垂直平分线与直线m的交点.
作线段AB的中垂线.
∵MN垂直平分线段AB,
∴PA=PB(线段的垂直平分线上的点到线段的两个端点的距离相等).
2.(1)解:如图所示:EF即为线段AC的垂直平分线;
(2)∵DE是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C=26°,
∵∠B=60°,∠C=26°,
∴∠BAC=180°-26°-60°=94°,
∵AF平分∠BAC,
∴∠FAC=12∠BAC=47°,
∴∠DAE=21°.
3.(1)证明:∵AC⊥BC,BD⊥AD,
∴∠C=∠D=90°,
∴在Rt△ACB和Rt△BDA中,AC=BDAB=BA,
∴Rt△ACB≌Rt△BDAHL,
∴BC=AD;
(2)证明:∵Rt△ACB≌Rt△BDA,
∴∠CAB=∠DBA,
∴OA=OB,
∴点O在线段AB的垂直平分线上.
4.(1)∵AC=AB,DC=DB,AD=AD,
∴△ACD≌△ABD(SSS);
(2)∵△ACD≌△ABD,
∴∠CAO=∠BAO.
又∵AC=AB,AO=AO,
∴△CAO≌△BAO(SAS),
∴∠COA=∠BOA=90°,CO=BO,
∴AD垂直平分BC.
5.(1)
如图所示,点D、H即为所求
(2)
∵DH垂直平分BC,
∴DC=DB,
∴∠B=∠DCB,
∵∠B+∠A=90°,∠DCB+∠DCA=∠ACB=90°,
∴∠A=∠DCA,
∴DC= DA,
∴△BCD的周长=DC+DB+BC=DA+DB+BC=AB+BC=8+5=13.
6.(1)作法:如图所示,
①连接PC(用虚线),
②作PC的垂直平分线交AC于E,
③标出点E即为所求,
(2)∵PE=CE,
∴AE+EP=AC,
∴△APE的周长=AP+AE+PE=AP+AC=3+6=9.
7.(1)证明:∵CB=CD,CE⊥BD,
∴DH=BH,∠DCH=∠BCH,
∴CE垂直平分BD,
∴ED=EB,
∴∠DEH=∠BEH,
∵DE∥BC,
∴∠DEC=∠BCE,
∴∠BEC=∠BCE,
∴BE=BC.
(2)DE,CF,
理由:∵DE垂直平分AC,
∴AE=EC,DA=DC,
∴∠AED=∠CED,∠ACE=∠EAC
又∵CD=CB且CE⊥BD,
∴HB=HD,CE垂直平分DB,
∴CB=CD=DA,DE=BE,
∴∠DEC=∠BEC,
∴∠AED=∠CED=∠BEC,
又∵∠AED+∠CED+∠BEC=180°,
∴∠AED=∠CED=∠BEC=13×180°=60°;
∴∠ACE=∠EAC=∠EBD=∠EDB=30°,
在△ACE与△ABF中,
∠ACE=∠ABF∠CAE=∠BAFAE=AF,
∴△ABF≌△ACEAAS,
∴AC=AB,
又∵AE=AF,
∴AB-AE=AC-AF,
即BE=CF.
8.(1)证明:如图,连接DN,
∵AO平分∠BAC,
∴∠BAD=∠CAD,
∵l⊥AO,
∴∠AHN=∠AHC=90°,
∴∠ANH=∠ACH,
∴AN=AC,
∴NH=CH,
∴DN=DC,
∴∠DNH=∠DCH,
∴∠AND=∠ACB,
∵∠ACB=2∠B,
∴∠AND=2∠B,
∵∠AND=∠B+∠BDN,
∴∠B=∠BDN,
∴DN=BN,
∴CD=BN;
(2)解:BN=CD+CE,理由如下:
如图,过点C作CF⊥AD交AB于点F,交AD于点G,连接DF,
∵AO平分∠BAC,
∴∠BAD=∠CAD,
∵l⊥AO,
∴∠AHN=∠AHE=90°,
∴∠ANH=∠AEH,
∴AN=AE,
同理∠AFC=∠ACF,
∴AF=AC,
∴FG=CG,FN=CE,
∴DF=DC,
∴∠DFC=∠DCF,
∴∠AFD=∠ACB,
∵∠ACB=2∠B,
∴∠AFD=2∠B,
∵∠AFD=∠B+∠BDF,
∴∠B=∠BDF,
∴DF=BF,
∴CD=BF,
∴BN=BF+FN=CD+CE.
9.(1)如图1,连接BE,
∵△ABC和△CEF都是等边三角形,
∴AB=BC=AC,CE=CF,∠BCA=∠FCE=60°,
∴∠BCA-∠ECA=∠FCE-∠ECA,
即∠BCE=∠ACF,
在△BCE和△ACF中,
CB=CA∠BCE=∠ACFCE=CF,
∴△BCE≌△ACFSAS,
∴EB=FA,
∵AB=AC,
∴AD是线段BC的垂直平分线,
∴EB=EC,
∴EC=FA,
又∵EC=FC,
∴FA=FC,
∴点F在线段AC的垂直平分线上,
∵BA=BC,
∴点B在线段AC的垂直平分线上,
∴BF垂直平分AC,
(2)如图2,E'F∥BC,理由如下:
由CE关于直线AC对称的线段CE'可知:CE=CE',∠1=∠2,
∵△ABC,△CEF都是等边三角形,
∴CE=CF,∠BCA=∠FCE=60°,
∴CF=CE',∠BCE'=∠BCA+∠2=60°+∠2,
∠3=∠ECF-∠1-∠2=60°-2∠2,
∴∠CE'F=∠CFE',
∵∠CE'F+∠CFE'+∠3=180°,
∴∠CE'F=180°-∠32=180°-(60°-2∠2)2=60°+∠2,
又∵∠BCE'=60°+∠2,
∴∠CE'F=∠BCE',
∴E'F∥BC.
相关试卷
这是一份北师大版(2024)八年级下册第一章 三角形的证明3 线段的垂直平分线课时练习,共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份北师大版八年级下册3 线段的垂直平分线复习练习题,共6页。试卷主要包含了如图是按以下步骤作图等内容,欢迎下载使用。
这是一份北师大版八年级下册3 线段的垂直平分线课时训练,共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。










