江西省赣州市经开区期中考试2024-2025学年八年级上学期11月期中数学试题 -（原卷版）-A4

这是一份江西省赣州市经开区期中考试2024-2025学年八年级上学期11月期中数学试题 -（原卷版）-A4，共7页。
一、选择题（共6小题，满分18分，每小题3分）
1. 下列交通标志图形中，轴对称图形的是（ ）
A. B.
C. D.
2. 如图，在中，边上的高作法正确的是（ ）
A. B. C. D.
3. 点关于x轴对称点的坐标是（ ）
A. B. C. D.
4. 如图，是一个任意角，在边，上分别取移动角尺，使角尺两边相同的刻度分别与，重合，过角尺顶点的射线便是的平分线，做法用得到三角形全等的判定定方法是（ ）
A. B. C. D.
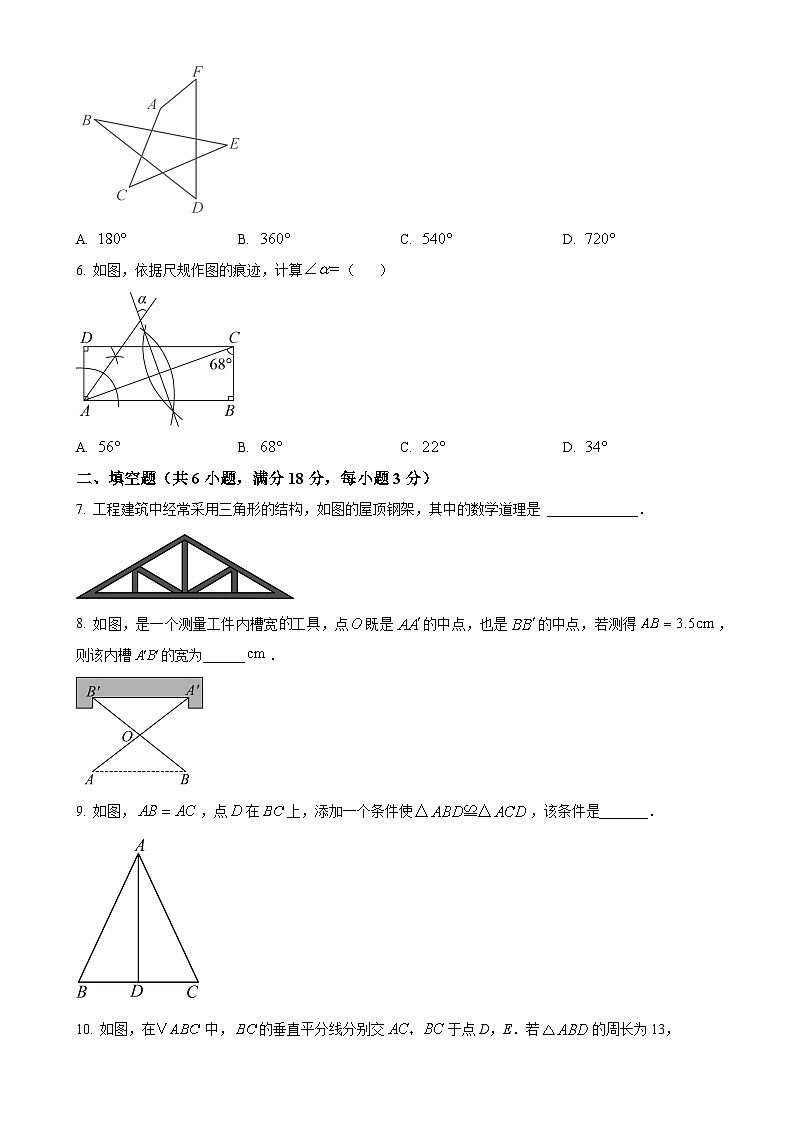
5. 平面上、、、、、六点，构成如图所示的图形，则度数是（ ）
A. B. C. D.
6. 如图，依据尺规作图的痕迹，计算（ ）
A. B. C. D.
二、填空题（共6小题，满分18分，每小题3分）
7. 工程建筑中经常采用三角形的结构，如图的屋顶钢架，其中的数学道理是 _____________．
8. 如图，是一个测量工件内槽宽工具，点既是的中点，也是的中点，若测得，则该内槽的宽为______．
9. 如图，，点在上，添加一个条件使，该条件_______．
10. 如图，在中，的垂直平分线分别交于点D，E．若的周长为13，，则的周长为______．
11. 我国古代天文学确定方向的方法中蕴藏了平行线的作图法．如《淮南子天文训》中记载：“正朝夕：先树一表东方；操一表却去前表十步，以参望日始出北廉．日直入，又树一表于东方，因西方之表，以参望日方入北康．则定东方两表之中与西方之表，则东西也．”如图，用几何语言叙述作图方法：已知直线和直线外一定点，过点作直线与平行．
（1）以为圆心，单位长为半径作圆，交直线于点，；
（2）分别在的延长线及上取点，，使；
（3）连接，取其中点，过，两点确定直线，则直线．
按以上作图顺序，若，则____．
12. 如图，的顶点分别为A0,3，，，且与全等（点与点不重合），则点坐标可以是___________．
三、解答题（本大题共5小题，每小题6分，共30分）
13. （1）已知一个多边形的内角和是它的外角和的3倍，求这个多边形的边数；
（2）如图，点在上，点在上，．求证：．

14. 在中，，，．
（1）m的取值范围为 ；．
（2）若是等腰三角形，求的周长．
15. 求证：三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等．
请把下面的说理过程补充完整．
已知：如图，在中，分别作边、边的垂直平分线，两线相交于点，分别交边、边于点、．
求证：、、的垂直平分线相交于点，___________
证明：连接、、．
点是边垂直平线上的一点，___________（ ）
同理可得，___________．（等量代换）．
点是___________边垂直平线上的一点（ ）
、、的垂直平分线相交于点．

16. 如图，在正五边形中，请仅用无刻度的直尺分别按下列要求作图（保留作图痕迹）．
（1）如图1，过点A求作此正五边形的对称轴；
（2）如图2，点M在AB上，且，在AE边上求作一点N，使．
17. 如图，在中，，．
（1）写出图中三对相等的角___________．
（2）求的大小．
四、解答题（本大题共3小题，每小题8分，共24分）
18. 如图，在中，，平分，平分，过点O作的平行线与，分别相交于点M，N．若．

（1）求的度数；
（2）求的周长．
19. 如图，在平面直角坐标系中，的三个顶点分别为、、．
（1）请在图中作出关于轴的轴对称图形（、、的对称点分别是、、），并直接写出、、的坐标；
（2）求的面积．
20. 如图，在中，平分，于点E，点F在上，．
（1）求证：．
（2）若，求的长．
五、解答题（本大题共2小题，每小题9分，共18分）
21. 如图，在中，为边上的高，为的角平分线．
（1）若，，求的度数；
（2）若，还能求的度数吗？若能，请写出求解过程；若不能，请说明理由．
22. 【阅读理解】
中线是三角形中重要线段之一、在利用中线解决几何问题时，当条件中出现“中点”、“中线”等条件时，可以考虑做辅助线，即把中线延长一倍，通过构造全等三角形，把分散的已知条件和所要求的结论集中到同一个三角形中，从而运用全等三角形的有关知识来解决问题，这种作辅助线的方法称为“倍长中线法”．
【小试牛刀】
如图1，在中，，，是的中点，求边上的中线的取值范围．
（1）小明在组内经过合作交流，得到了如下的解决方法：延长到点，使，连接．可以判定，请写出证明过程．
（2）利用（1）中的结论，写出中线的取值范围是___________（请直接写出答案）．
【实践应用】
（3）为了测量学校旗杆和教学楼顶端之间的距离，学习小组设计了如图2所示的测量方案，他们首先取地面的中点，此时用测角仪恰好测得，并量得旗杆高度，教学楼高度，求的长．
六、解答题（本大题12分）
23. 【课题学习】
三角形是平面几何最基本的图形之一，构造全等三角形是几何学中的重要问题．一些较复杂的问题，只要依据条件构造合适的全等三角形，把条件相对集中起来，再进行等量代换，就可以化难为易了．
【初步感知】
（1）如图1，在中，，点在边上，，若在上取一点，使得．写出图中一对全等的三角形是___________．
【深入探究】
（2）如图2，在中，，点、坐标分别是、0,4，边交轴于点，若，求的值；
【拓展探索】
（3）如图3，在和中，，，射线交线段于点，求证：点为线段的中点．