高中数学公式及知识点总结大全（精华版）-学案

这是一份高中数学公式及知识点总结大全（精华版）-学案，共10页。学案主要包含了函数，三角函数，数列，不等式，解析几何，立体几何，概率统计，复数等内容，欢迎下载使用。
一、函数、导数
1、函数的单调性
(1)设那么
上是增函数；
上是减函数.
(2)设函数在某个区间内可导，若，则为增函数；若，则为减函数.
2、函数的奇偶性
对于定义域内任意的，都有，则是偶函数；
对于定义域内任意的，都有，则是奇函数。
奇函数的图象关于原点对称，偶函数的图象关于y轴对称。
3、函数在点处的导数的几何意义
函数在点处的导数是曲线在处的切线的斜率，相应的切线方程是.
*二次函数： （1）顶点坐标为；（2）焦点的坐标为
4、几种常见函数的导数
①；②； ③；④；
⑤；⑥； ⑦；⑧
5、导数的运算法则
（1）. （2）. （3）.
6、会用导数求单调区间、极值、最值
7、求函数的极值的方法是：解方程．当时：
(1) 如果在附近的左侧，右侧，那么是极大值；
(2) 如果在附近的左侧，右侧，那么是极小值．
指数函数、对数函数
分数指数幂
(1)（，且）.
(2)（，且）.
根式的性质
（1）当为奇数时，；
当为偶数时，.
有理指数幂的运算性质
(1) .
(2) .
(3).
注： 若a＞0，p是一个无理数，则ap表示一个确定的实数．上述有理指数幂的运算性质，对于无理数指数幂都适用.
.指数式与对数式的互化式: .
.对数的换底公式 : (,且,,且, ).
对数恒等式：(,且, ).
推论 (,且, ).
常见的函数图象
二、三角函数、三角变换、解三角形、平面向量
8、同角三角函数的基本关系式
，=.
9、正弦、余弦的诱导公式（奇变偶不变，符号看象限）
的正弦、余弦，等于的同名函数，前面加上把看成锐角时该函数的符号；
的正弦、余弦，等于的余名函数，前面加上把看成锐角时该函数的符号。
，，．
，，．
，，．
，，．
口诀：函数名称不变，符号看象限．
，．，．
口诀：正弦与余弦互换，符号看象限．
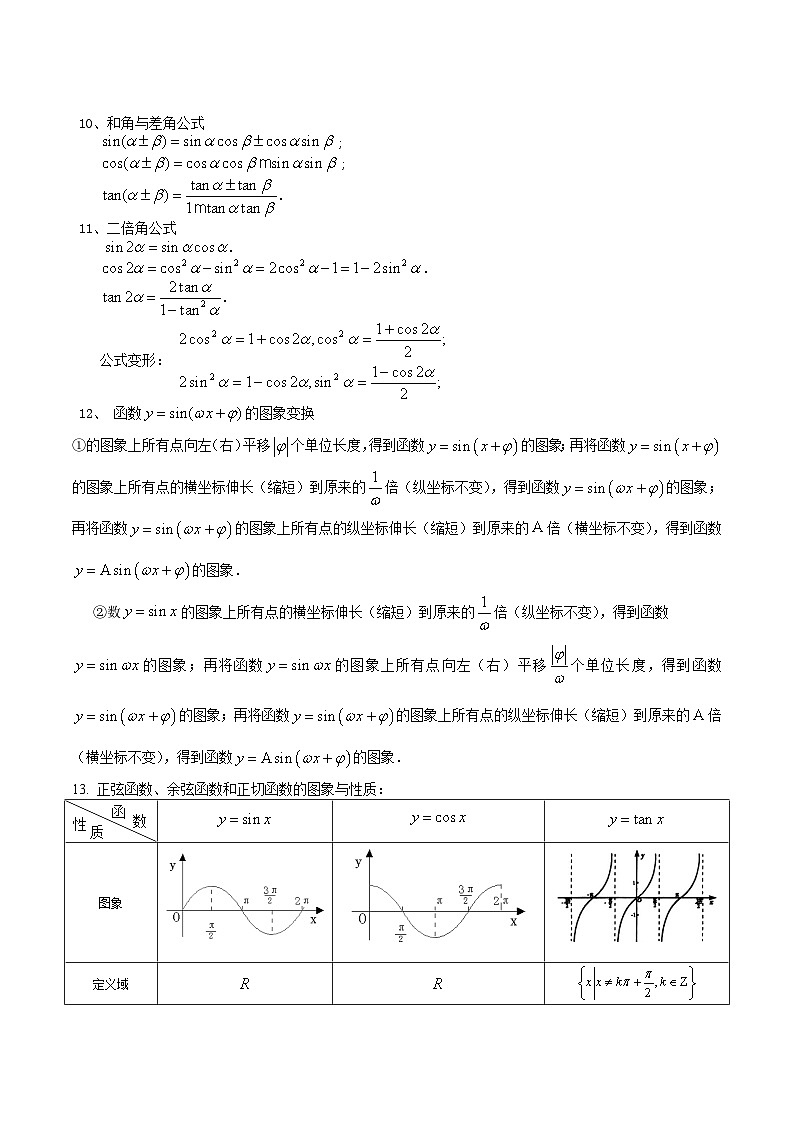
10、和角与差角公式
;
;
.
11、二倍角公式
.
.
.
公式变形：
12、 函数的图象变换
①的图象上所有点向左（右）平移个单位长度，得到函数的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的倍（纵坐标不变），得到函数的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的倍（横坐标不变），得到函数的图象．
②数的图象上所有点的横坐标伸长（缩短）到原来的倍（纵坐标不变），得到函数
的图象；再将函数的图象上所有点向左（右）平移个单位长度，得到函数的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的倍（横坐标不变），得到函数的图象．
13. 正弦函数、余弦函数和正切函数的图象与性质：
14、辅助角公式
其中
15.正弦定理 ：（R为外接圆的半径）.
16.余弦定理
;;.
17.面积定理
（1）（分别表示a、b、c边上的高）.
（2）.
18、三角形内角和定理
在△ABC中，有
.
19、与的数量积(或内积)
20、平面向量的坐标运算
(1)设A，B,则.
(2)设=,=，则=.
(3)设=，则
21、两向量的夹角公式
设=,=，且，则
(=,=).
22、向量的平行与垂直
设=,=，且
.
.
*平面向量的坐标运算
(1)设=,=，则+=.
(2)设=,=，则-=.
(3)设A，B,则.
(4)设=，则=.
(5)设=,=，则·=.
三、数列
23、数列的通项公式与前n项的和的关系
( 数列的前n项的和为).
24、等差数列的通项公式
；
25、等差数列其前n项和公式为
.
26、等比数列的通项公式
；
27、等比数列前n项的和公式为
或 .
四、不等式
28、。必须满足一正（都是正数）、二定（是定值或者是定值）、三相等（时等号成立）才可以使用该不等式）
（1）若积是定值，则当时和有最小值；
（2）若和是定值，则当时积有最大值.
五、解析几何
29、直线的五种方程
（1）点斜式 (直线过点，且斜率为)．
（2）斜截式 (b为直线在y轴上的截距).
（3）两点式 ()(、 ()).
(4)截距式 (分别为直线的横、纵截距，)
（5）一般式 (其中A、B不同时为0).
30、两条直线的平行和垂直
若，
①;
②.
31、平面两点间的距离公式
(A，B).
32、点到直线的距离
(点,直线：).
33、 圆的三种方程
（1）圆的标准方程 .
（2）圆的一般方程 (＞0).
（3）圆的参数方程 .
* 点与圆的位置关系：点与圆的位置关系有三种
若，则点在圆外;点在圆上;点在圆内.
34、直线与圆的位置关系
直线与圆的位置关系有三种:
;
;
. 弦长=
其中.
35、椭圆、双曲线、抛物线的图形、定义、标准方程、几何性质
椭圆：，，离心率0,b>0)，，离心率，渐近线方程是.
抛物线：，焦点,准线。抛物线上的点到焦点距离等于它到准线的距离.
36、双曲线的方程与渐近线方程的关系
(1）若双曲线方程为渐近线方程：.
(2)若渐近线方程为双曲线可设为.
(3)若双曲线与有公共渐近线，可设为（，焦点在x轴上，，焦点在y轴上）.
37、抛物线的焦半径公式
抛物线焦半径.（抛物线上的点到焦点距离等于它到准线的距离。）
38、过抛物线焦点的弦长.
六、立体几何
函
数
性
质

图象
定义域
值域
最值
当时，；当
时，．
当时，
；当
时，．
既无最大值也无最小值
周期性
奇偶性
奇函数
偶函数
奇函数
单调性
在
上是增函数；在
上是减函数．
在上是增函数；在
上是减函数．
在
上是增函数．
对称性
对称中心
对称轴
对称中心
对称轴
对称中心
无对称轴
39.证明直线与直线的平行的思考途径
（1）转化为判定共面二直线无交点；
（2）转化为二直线同与第三条直线平行；
（3）转化为线面平行；
（4）转化为线面垂直；
（5）转化为面面平行.
40．证明直线与平面的平行的思考途径
（1）转化为直线与平面无公共点；
（2）转化为线线平行；
（3）转化为面面平行.
41.证明平面与平面平行的思考途径
（1）转化为判定二平面无公共点；
（2）转化为线面平行；
（3）转化为线面垂直.
42．证明直线与直线的垂直的思考途径
（1）转化为相交垂直；
（2）转化为线面垂直；
（3）转化为线与另一线的射影垂直；
（4）转化为线与形成射影的斜线垂直.
43．证明直线与平面垂直的思考途径
（1）转化为该直线与平面内任一直线垂直；
（2）转化为该直线与平面内相交二直线垂直；
（3）转化为该直线与平面的一条垂线平行；
（4）转化为该直线垂直于另一个平行平面。
44．证明平面与平面的垂直的思考途径
（1）转化为判断二面角是直二面角；
（2）转化为线面垂直；
45、柱体、椎体、球体的侧面积、表面积、体积计算公式
圆柱侧面积=，表面积=
圆椎侧面积=，表面积=
（是柱体的底面积、是柱体的高）.
（是锥体的底面积、是锥体的高）.
球的半径是，则其体积,其表面积．
46、若点A，点B，则=
47、点到平面距离的计算（定义法、等体积法）
48、直棱柱、正棱柱、长方体、正方体的性质：侧棱平行且相等，与底面垂直。
正棱锥的性质：侧棱相等，顶点在底面的射影是底面正多边形的中心。
七、概率统计
49、平均数、方差、标准差的计算
平均数: 方差:
标准差:
50、回归直线方程 （了解即可）
，其中.经过（，）点。
51、独立性检验 （了解即可）
52、古典概型的计算（必须要用列举法、列表法、树状图的方法把所有基本事件表示出来，不重复、不遗漏）
八、复数
53、复数的除法运算
.
54、复数的模==.
55、复数的相等：.（）
56、复数的模（或绝对值）==.
57、复数的四则运算法则
(1);
(2);
(3);
(4).
58、复数的乘法的运算律
对于任何，有
交换律:.
结合律:.
分配律: .
九、参数方程、极坐标化成直角坐标
59、
十、命题、充要条件
充要条件（记表示条件，表示结论）
（1）充分条件：若，则是充分条件.
（2）必要条件：若，则是必要条件.
（3）充要条件：若，且，则是充要条件.
注：如果甲是乙的充分条件，则乙是甲的必要条件；反之亦然.
60、真值表
十一、直线与平面的位置关系
空间点、直线、平面之间的位置关系
三个公理：
（1）公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内
（2）公理2：过不在一条直线上的三点，有且只有一个平面。
（3）公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。
空间中直线与直线之间的位置关系
1 空间的两条直线有如下三种关系：
共面直线
相交直线：同一平面内，有且只有一个公共点；
平行直线：同一平面内，没有公共点；
异面直线： 不同在任何一个平面内，没有公共点。
2 公理4：平行于同一条直线的两条直线互相平行。
3 等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补
4 注意点：
① a'与b'所成的角的大小只由a、b的相互位置来确定，与O的选择无关，为简便，点O一般取在两直线中的一条上；
② 两条异面直线所成的角θ∈ ；
③ 当两条异面直线所成的角是直角时，我们就说这两条异面直线互相垂直，记作a⊥b；
④ 两条直线互相垂直，有共面垂直与异面垂直两种情形；
⑤ 计算中，通常把两条异面直线所成的角转化为两条相交直线所成的角。
空间中直线与平面、平面与平面之间的位置关系
1、直线与平面有三种位置关系：
（1）直线在平面内 —— 有无数个公共点
（2）直线与平面相交 —— 有且只有一个公共点
（3）直线在平面平行 —— 没有公共点
直线、平面平行的判定及其性质
直线与平面平行的判定
1、直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。
简记为：线线平行，则线面平行。
平面与平面平行的判定
1、两个平面平行的判定定理：一个平面内的两条交直线与另一个平面平行，则这两个平面平行。
2、判断两平面平行的方法有三种：
（1）用定义；
（2）判定定理；
（3）垂直于同一条直线的两个平面平行。
直线与平面、平面与平面平行的性质
1、定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行。
简记为：线面平行则线线平行。
2、定理：如果两个平面同时与第三个平面相交，那么它们的交线平行。
直线、平面垂直的判定及其性质
直线与平面垂直的判定
1、定义：如果直线L与平面α内的任意一条直线都垂直，我们就说直线L与平面α互相垂直，记作L⊥α，直线L叫做平面α的垂线，平面α叫做直线L的垂面。如图，直线与平面垂直时,它们唯一公共点P叫做垂足。
2、判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。
平面与平面垂直的判定
1、二面角的概念：表示从空间一直线出发的两个半平面所组成的图形
A
梭 l β
B
α
2、二面角的记法：二面角α-l-β或α-AB-β
3、两个平面互相垂直的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直。
直线与平面、平面与平面垂直的性质
1、定理：垂直于同一个平面的两条直线平行。
2性质定理： 两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。
ｐ
ｑ
非ｐ
ｐ或ｑ
ｐ且ｑ
真
真
假
真
真
真
假
假
真
假
假
真
真
真
假
假
假
真
假
假