人教版数学七年级下册期末培优解答题压轴题训练（四）（2份，原卷版+解析版）

这是一份人教版数学七年级下册期末培优解答题压轴题训练（四）（2份，原卷版+解析版），文件包含人教版数学七年级下册期末培优解答题压轴题训练四原卷版doc、人教版数学七年级下册期末培优解答题压轴题训练四解析版doc等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。
解答题解题策略：（1）常见失分因素：①对题意缺乏正确的理解，应做到慢审题快做题；②公式记忆不牢，考前一定要熟悉公式、定理、性质等；③思维不严谨，不要忽视易错点；④解题步骤不规范，一定要按课本要求，否则会因不规范答题而失分，避免“对而不全”，如解概率题时，要给出适当的文字说明，不能只列几个式子或单纯的结论，表达不规范、字迹不工整等非智力因素会影响阅卷老师的“感情分”；⑤计算能力差导致失分多，会做的试题一定不能放过，不能一味求快，⑥轻易放弃试题，难题不会做时，可分解成小问题，分步解决，如最起码能将文字语言翻译成符号语言、设应用题未知数、设轨迹的动点坐标等，都能拿分。也许随着这些小步骤的罗列，还能悟出解题的灵感。
（2）何为“分段得分”：对于同一道题目，有的人理解的深，有的人理解的浅；有的人解决的多，有的人解决的少。为了区分这种情况，中考的阅卷评分办法是懂多少知识就给多少分。这种方法我们叫它“分段评分”，或者“踩点给分”——踩上知识点就得分，踩得多就多得分。与之对应的“分段得分”的基本精神是，会做的题目力求不失分，部分理解的题目力争多得分。对于会做的题目，要解决“会而不对，对而不全”这个老大难问题。有的考生拿到题目，明明会做，但最终答案却是错的——会而不对。有的考生答案虽然对，但中间有逻辑缺陷或概念错误，或缺少关键步骤——对而不全。因此，会做的题目要特别注意表达的准确、考虑的周密、书写的规范、语言的科学，防止被“分段扣分”。经验表明，对于考生会做的题目，阅卷老师则更注意找其中的合理成分，分段给点分，所以“做不出来的题目得一二分易，做得出来的题目得满分难”。
对绝大多数考生来说，更为重要的是如何从拿不下来的题目中分段得点分。我们说，有什么样的解题策略，就有什么样的得分策略。把你解题的真实过程原原本本写出来，就是“分段得分”的全部秘密。
①缺步解答：如果遇到一个很困难的问题，确实啃不动，一个聪明的解题策略是，将它们分解为一系列的步骤，或者是一个个小问题，先解决问题的一部分，能解决多少就解决多少，能演算几步就写几步，尚未成功不等于失败。特别是那些解题层次明显的题目，或者是已经程序化了的方法，每一步得分点的演算都可以得分，最后结论虽然未得出，但分数却已过半，这叫“大题拿小分”。
②跳步答题：解题过程卡在某一过渡环节上是常见的。这时，我们可以先承认中间结论，往后推，看能否得到结论。如果不能，说明这个途径不对，立即改变方向；如果能得出预期结论，就回过头来，集中力量攻克这一“卡壳处”。由于考试时间的限制，“卡壳处”的攻克如果来不及了，就可以把前面的写下来，再写出“证实某步之后，继续有……”一直做到底。也许，后来中间步骤又想出来，这时不要乱七八糟插上去，可补在后面。若题目有两问，第一问想不出来，可把第一问作为“已知”，先做第二问，这也是跳步解答。
③退步解答：“以退求进”是一个重要的解题策略。如果你不能解决所提出的问题，那么，你可以从一般退到特殊，从抽象退到具体，从复杂退到简单，从整体退到部分，从较强的结论退到较弱的结论。总之，退到一个你能够解决的问题。为了不产生“以偏概全”的误解，应开门见山写上“本题分几种情况”。这样，还会为寻找正确的、一般性的解法提供有意义的启发。
④辅助解答：一道题目的完整解答，既有主要的实质性的步骤，也有次要的辅助性的步骤。实质性的步骤未找到之前，找辅助性的步骤是明智之举。如：准确作图，把题目中的条件翻译成数学表达式，设应用题的未知数等。答卷中要做到稳扎稳打，字字有据，步步准确，尽量一次成功，提高成功率。试题做完后要认真做好解后检查，看是否有空题，答卷是否准确，所写字母与题中图形上的是否一致，格式是否规范，尤其是要审查字母、符号是否抄错，在确信万无一失后方可交卷。
一、解答题
我们用表示不大于a的最大整数，例如：，，；用表示大于a的最小整数，例如：，，据此解决下列问题：
______，________；
若，则x的取值范围是______；若，则y的取值范围是______；
已知x，y满足方程组求x，y的取值范围．
【答案】解：；4；
；；
解方程组得：
故x，y的取值范围分别为，．
【知识点】一元一次不等式组的应用、一元一次不等式组的解法
【解析】
【分析】
本题考查了一元一次不等式组的应用，解答本题的关键是读懂题意，根据题目所给的信息进行解答．
根据题目所给信息求解；
根据，，，可得中的，根据表示大于a的最小整数，可得中，；
先求出和的值，然后求出x和y的取值范围．
【解答】
解：由题意得：，；
故答案为；4．
，
的取值范围是；
，
的取值范围是；
故答案为；．
见答案．
已知：点A、C、B不在同一条直线上，．
如图，当，时，求的度数；
如图，AQ、BQ分别为、的平分线所在直线，试探究与的数量关系；
如图，在的前提下，且有，，直接写出：：的值．
【答案】解：在图中，过点C作，则．
，
，，
．
在图2中，过点Q作，则．
，，
，．
平分，BQ平分，
，，
．
，
．
，
，，
．
，
．
又，
，即，
，，
，
：：：：：2：2．
【知识点】平行线的性质
【解析】本题考查了平行线的性质、邻补角、角平分线以及垂线．
过点C作，则，根据平行线的性质可得出、，将其代入即可求出的度数；
过点Q作，则，根据平行线的性质、角平分线的定义可得出，结合的结论可得出；
由的结论可得出，由可得出，联立可求出、的度数，再结合的结论可得出的度数，将其代入：：中可求出结论．
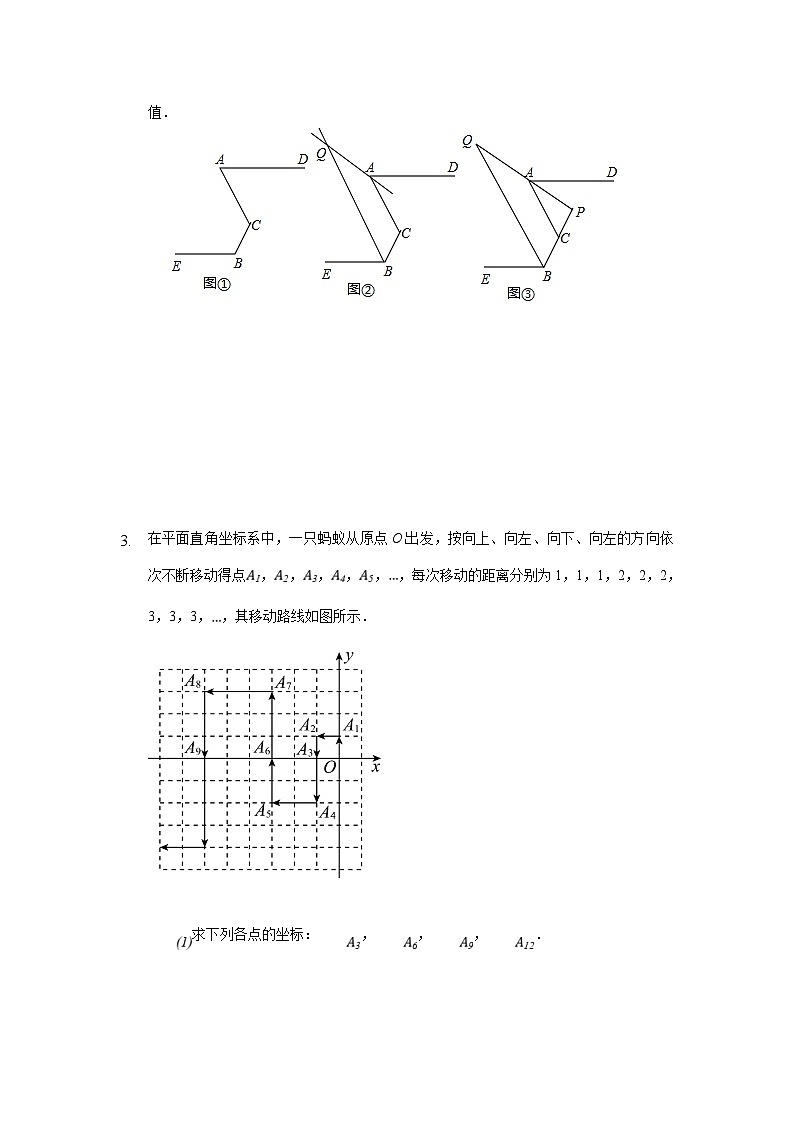
在平面直角坐标系中，一只蚂蚁从原点O出发，按向上、向左、向下、向左的方向依次不断移动得点，，，，，，每次移动的距离分别为1，1，1，2，2，2，3，3，3，，其移动路线如图所示．
求下列各点的坐标：，，，．
写出点的坐标为正整数．
求蚂蚁从原点O到点移动的路程．
【答案】解：根据图形可知，，，；
由可知 ，
，
，
则的坐标为；
蚂蚁从原点O到点移动的距离是．
【知识点】平面直角坐标系中点的坐标、代数式求值
【解析】本题考查了点坐标的规律变化，解答本题的关键是仔细观察图象，得到点的变化规律，难度一般．
根据已知的坐标系，即可写出要求的三个点的坐标；
总结规律，问题便可解答；
利用数轴上两点之间距离的求法可得原点O到点
甲车和乙车从A、B两地同时出发，沿同一线路相向匀速行驶，出发后两车在C地相遇，相遇时甲车比乙车少走，相遇后乙车到达A地．
两车的行驶速度分别是多少？
相遇后，若甲车想在乙车到达A地的同时到达B地，那么甲车的行驶速度要比原来增加多少？
探索：若从C地到B地的路段中，有一部分限速，其余部分限速，甲车从C地到B地时，在相应路段均以限速行驶不超速也不低于限速，则恰好能在乙车到达A地的同时到达B地，求C地到B地间限速和限速的路程各是多少？
【答案】解：设甲、乙两车行驶的速度分别是每小时x千米、y千米，由题意得
，
解得．
答：甲、乙两车行驶的速度分别是每小时80千米、100千米；


千米小时．
答：甲车的行驶速度要比原来增加．
设C地到B地间限速的路程为a千米，由题意得
，
解得：，
则千米．
答：C地到B地间限速的路程为108千米，则限速的路程为42千米．
【知识点】一元一次方程的应用、二元一次方程组的应用
【解析】设甲、乙行驶的速度分别是每小时x千米、y千米，根据题意列出二元一次方程组，求出x和y的值即可；
求得甲车需要行的路程，再除以需要的时间求得现在的速度，减去原来的速度即可；
设C地到B地间限速的路程为a千米，则限速的路程为千米，根据行驶的时间和为小时，列出方程解决问题即可．
此题考查二元一次方程组与一元一次方程的实际运用，理解题意，找出题目蕴含的数量关系是解决问题的关键．
纸箱厂用如图1所示的长方形和正方形纸板，做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒给定的长方形和正方形纸板都不用裁剪．
若有150张正方形硬纸片和300张长方形硬纸片恰好全部用完，可供制作竖式与横式纸盒各多少个？
现有正方形纸板172张，长方形纸板330张．若要生产两种纸盒共100个，有哪几种生产方案？
若有正方形纸板112张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完．若已知，则a的值是____直接写答案
【答案】解：设做竖式纸盒x个，横式纸盒y个，
根据题意得，
解得．
答：可供制作竖式与横式纸盒各是30个、60个；
设做竖式纸盒x个，
根据题意得，
解得，
不等式组的解集是，
整数，29，30，所以有三种方案：
、208．
【知识点】一元一次不等式组的应用、二元一次方程组的应用
【解析】
【分析】
本题考查二元一次方程组及一元一次不等式组的应用．
设做竖式纸盒x个，横式纸盒y个，根据题意得二元一次方程组，解方程组即可；
根据题意直接列出一元一次不等式组，解不等式组，又知x只能为正整数，故共有三种生产方案；
根据前面步骤，可直接求出a值．
【解答】
解：见答案；
见答案；
根据题意得，
解得：，
，且y为整数，
所以a的值是203，208．
故答案为203，208．
已知 中，，，D 为BC 边延长线上一点，BM 平分，E 为射线BM 上一点．
如图1，连接CE，
若，求 的度数；
若CE 平分，求 的度数．
若直线CE 垂直于 的一边，请直接写出 的度数．
【答案】解：，，
，
平分，
，
，
；
，，
，，
平分，CE平分，
，，
；
如图1，当时，
，
；
如图2，当于F时，
，
，
如图3，当时，
，，
．
【知识点】平行线的性质、垂线的相关概念及表示
【解析】本题考查了平行线的性质，角平分线的定义，垂直的定义，三角形的内角和，三角形的外角的性质，正确的画出图形是解题的关键．
根据三角形的内角和得到，由角平分线的定义得到，根据平行线的性质即可得到结论；
根据邻补角的定义得到，根据角平分线的定义得到，，根据三角形的外角的性质即可得到结论；
当时，如图2，当于F时，如图3，当时，根据垂直的定义和三角形的内角和即可得到结论．
如图，在平面直角坐标系中，四边形OABC为正方形，A点在x轴负半轴上，C点在y轴负半轴上，边长为有一动点P自O点出发，以每秒2个单位长度的速度沿运动，设P点运动时间为，则何时？并求出此时P点的坐标．
【答案】解：当点P在OA上时，不符合题意；
当P在AB上运动时，设，
，
，
，
，此时运动时间为：；
当P在BC上运动时，不存在；
当P在OC上运动时，设，
，
，
，
，此时运动时间为：；．
综上所述，当点P运动3s和7s时，点P的坐标分别为，．
【知识点】坐标与图形性质、三角形的面积
【解析】本题结合函数考查了正方形的性质、三角形面积．
注意数形结合思想、分类讨论思想的应用．分当P在OA上运动时，当P在AB上运动时，当P在BC上运动时，当P在OC上运动时四种情况进行分析得出结论．
如果3个数位相同的自然数m，n，k满足：，且k各数位上的数字全部相同，则称数m和数n是一对“黄金搭档数”例如：因为123，765，888都是三位数，，所以123和765是一对“黄金搭档数”再如：因为26，29，55都是两位数，，所以26和29是一对“黄金搭档数”．
若326与一个个位上的数字是3的数a是一对“黄金搭档数”，389与一个个位上的数字是8的数b是一对“黄金搭档数”，直接写出a和b的值；
若，，且，s和t是一对“黄金搭档数”，求这样的“黄金搭档数”一共有多少对
【答案】解： 326与一个个位上的数字是3的数a是一对“黄金搭档数”，
与a的和的个位数是9，且它们的和也是三位数，
一对黄金搭档数的和各位数上的数字全部相同，


同理可得：

综上：

的十位上的数字是相同的，

且都是两位数，，
s和t是一对“黄金搭档数”，
与t的和也是一个两位数，且各位数上的数字全部相同，


为正整数，
的可能的值为
综上可得：满足条件的数有10对，分别是：
当时，
当时， 或
当时， 或 或
当时， 或 或 或
综上：这样的“黄金搭档数”一共有10对．
【知识点】一元一次方程的解法、分类讨论思想、解二元一次方程、新定义型
【解析】本题考查的是新定义：黄金搭档数的定义的理解，利用定义借助方程，不等式，对变量的范围的理解进行分类讨论，解题的关键是弄懂题意，作出合适的分类．
由黄金搭档数的定义可得：解方程从而可得答案；
由可得的十位上的数字是相同的，再结合 可得：都是两位数，，由可得 结合x为正整数，再分类讨论可得答案．